可持久化数据结构

Change Log

• 2025.7.8 添加可持久化线段树

1. 线段树

1.1 主席树概述

主席树（Persistent Segment Tree），又称可持久化线段树，是一种保存历史版本的线段树数据结构。核心思想是"共用未修改节点"，通过新建修改路径上的节点来保存历史版本，空间复杂度为 O(n log n)。

典型应用场景：

• 区间第 K 大/小查询
• 区间不同数字个数
• 历史版本查询

---

1.2 核心思想

1. 动态开点：不预先分配完整树结构，按需创建节点
2. 节点复用：新版本只复制修改路径上的节点，未修改部分共享
3. 前缀和思想：用线段树维护序列前缀的信息

关键点：每个版本对应序列的一个前缀，区间查询通过两个版本相减实现

---

1.3算法流程（以区间第 K 小为例）

1.3.1 离散化

vector<int> nums = {1, 5, 2, 6, 3, 7, 4};  // 原始数组
vector<int> sorted = nums;
sort(sorted.begin(), sorted.end());
sorted.erase(unique(sorted.begin(), sorted.end()), sorted.end());

auto get_id = [&](int x) {
    return lower_bound(sorted.begin(), sorted.end(), x) - sorted.begin() + 1;
};

1.3.2 节点结构

struct Node {
    int l, r;  // 左右子节点指针
    int cnt;   // 当前值域内数字个数
} tree[MAXN * 20];  // 空间开20倍
int idx = 0;        // 节点计数器
int root[MAXN];     // 各版本根节点

1.3.3 建空树

int build(int l, int r) {
    int p = ++idx;
    if (l == r) return p;
    
    int mid = (l + r) >> 1;
    tree[p].l = build(l, mid);
    tree[p].r = build(mid + 1, r);
    return p;
}

root[0] = build(1, sorted.size());

1.3.4 插入新版本

int insert(int pre, int l, int r, int x) {
    int now = ++idx;
    tree[now] = tree[pre];  // 复制前驱节点
    
    if (l == r) {
        tree[now].cnt++;
        return now;
    }
    
    int mid = (l + r) >> 1;
    if (x <= mid) tree[now].l = insert(tree[pre].l, l, mid, x);
    else tree[now].r = insert(tree[pre].r, mid + 1, r, x);
    
    tree[now].cnt = tree[tree[now].l].cnt + tree[tree[now].r].cnt;
    return now;
}

// 为每个前缀创建版本
for (int i = 1; i <= n; i++)
    root[i] = insert(root[i - 1], 1, m, get_id(nums[i-1]));

1.3.5 查询区间第 K 小

int query(int u, int v, int l, int r, int k) {
    if (l == r) return l;
    
    int left_cnt = tree[tree[u].l].cnt - tree[tree[v].l].cnt;
    int mid = (l + r) >> 1;
    
    if (k <= left_cnt) 
        return query(tree[u].l, tree[v].l, l, mid, k);
    else 
        return query(tree[u].r, tree[v].r, mid + 1, r, k - left_cnt);
}

// 使用示例
int l = 2, r = 5, k = 3;  // 查询区间[2,5]第3小
int pos = query(root[r], root[l-1], 1, m, k);
cout << "第k小值: " << sorted[pos-1] << endl;

---

4. 原理解析

1. 版本生成
   
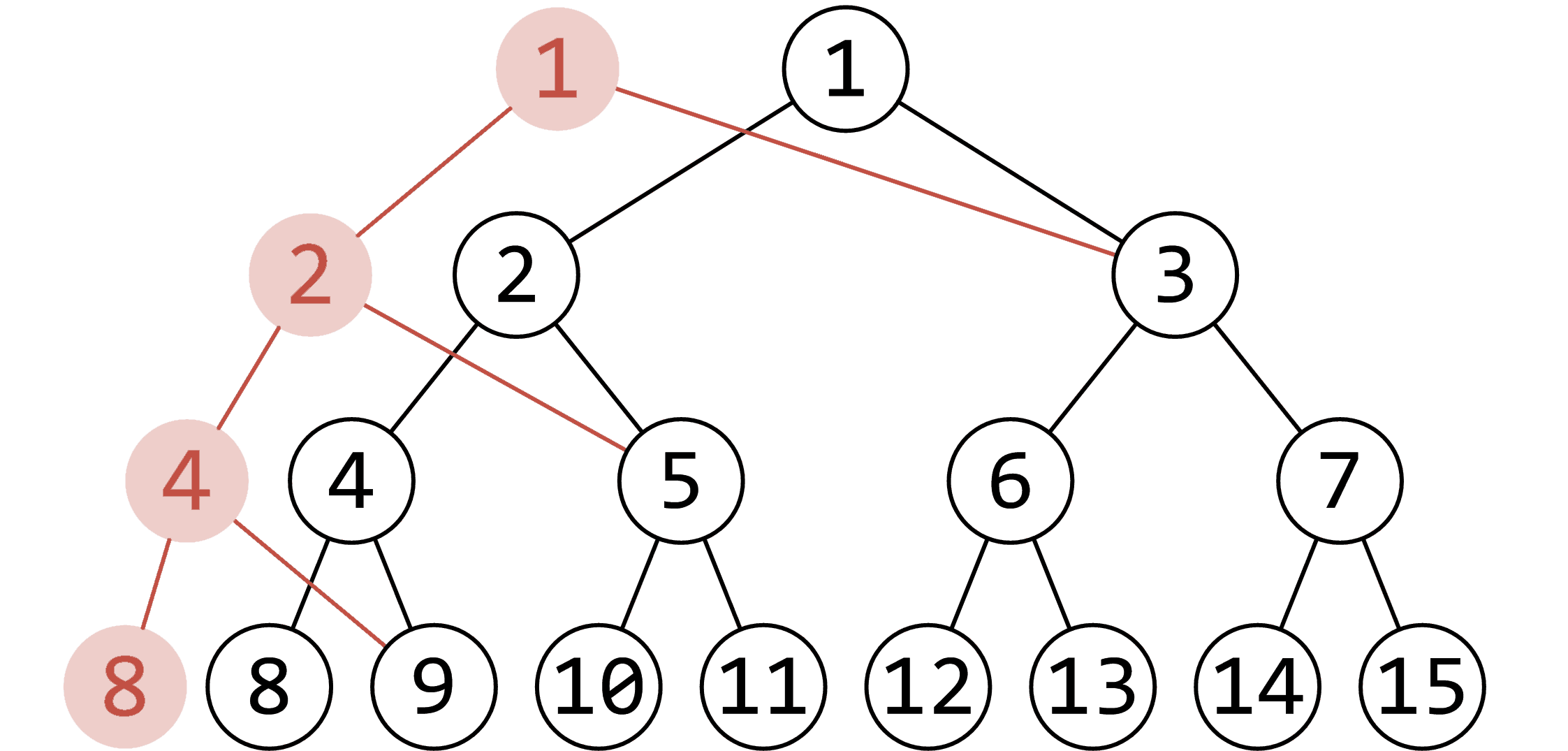
   每个新版本只修改 O(log n) 个节点

2. 区间查询原理
   query(root[R], root[L-1], ...)
   → 相当于 [1,R] - [1,L-1] = [L,R] 的信息

3. 第 K 小查询
   通过比较左右子树的元素个数决定搜索方向
   左子树元素数 >= K → 左子树
   左子树元素数 < K → 右子树找第 (K - left_cnt) 小

---

5. 复杂度分析

操作	时间复杂度	空间复杂度
建树	O(n)	O(n log n)
更新	O(log n)	O(log n)
查询	O(log n)	O(1)

空间计算：每次插入新增 O(log n) 节点 → 共 O(n log n)

---

6. 完整示例代码

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int MAXN = 1e5 + 10;
struct Node { int l, r, cnt; } tree[MAXN * 20];
int root[MAXN], idx;
vector<int> nums, sorted;

int build(int l, int r) {
    int p = ++idx;
    if (l == r) return p;
    int mid = (l + r) >> 1;
    tree[p].l = build(l, mid);
    tree[p].r = build(mid + 1, r);
    return p;
}

int insert(int pre, int l, int r, int x) {
    int now = ++idx;
    tree[now] = tree[pre];
    if (l == r) {
        tree[now].cnt++;
        return now;
    }
    int mid = (l + r) >> 1;
    if (x <= mid) tree[now].l = insert(tree[pre].l, l, mid, x);
    else tree[now].r = insert(tree[pre].r, mid + 1, r, x);
    tree[now].cnt = tree[tree[now].l].cnt + tree[tree[now].r].cnt;
    return now;
}

int query(int u, int v, int l, int r, int k) {
    if (l == r) return l;
    int left_cnt = tree[tree[u].l].cnt - tree[tree[v].l].cnt;
    int mid = (l + r) >> 1;
    if (k <= left_cnt) 
        return query(tree[u].l, tree[v].l, l, mid, k);
    else 
        return query(tree[u].r, tree[v].r, mid + 1, r, k - left_cnt);
}

int main() {
    // 示例数据
    nums = {1, 5, 2, 6, 3, 7, 4};
    sorted = nums;
    sort(sorted.begin(), sorted.end());
    sorted.erase(unique(sorted.begin(), sorted.end()), sorted.end());
    
    // 离散化函数
    auto get_id = [&](int x) {
        return lower_bound(sorted.begin(), sorted.end(), x) - sorted.begin() + 1;
    };
    
    // 建树
    int m = sorted.size();
    root[0] = build(1, m);
    
    // 创建各版本
    for (int i = 0; i < nums.size(); i++) 
        root[i + 1] = insert(root[i], 1, m, get_id(nums[i]));
    
    // 查询[2,5]区间第3小 (nums索引1~4)
    int l = 2, r = 5, k = 3;
    int pos = query(root[r], root[l - 1], 1, m, k);
    cout << "区间第" << k << "小: " << sorted[pos - 1] << endl;
    
    return 0;
}

7. 常见问题

1. 为什么需要离散化？
   原始数据范围大 → 离散化缩小值域 → 降低空间复杂度

2. 空间开多少合适？
   通常开 20倍 数据量：MAXN * 20
   （log₂(1e5) ≈ 17）

3. 如何扩展其他功能？

   • 区间不同数字个数：记录最后出现位置
   • 带修主席树：树状数组套主席树（树套树）

4. 查询时为什么是 k - left_cnt？
   当进入右子树时，说明第 K 小在右子树中
   → 在右子树中实际排名为 K - 左子树元素个数