[学习笔记] 前缀和与差分(深入探究)
前缀和
定义
前缀和可以简单理解为 \(\lceil\) 数列的前 \(n\) 项的和 \(\rfloor\),是一种重要的预处理方式,能大大降低查询的时间复杂度。
例题
有 \(n\) 个的正整数放到数组 \(a\) 里,现在要求一个新的数组 \(b\),新数组的第 \(i\) 个数 \(b_i\) 是原数组 \(a\) 第 \(1\) 到第 \(i\) 个数的和。
输入
5 1 2 3 4 5输出
1 3 6 10 15解题思路
递推:
B[1]=A[1],对于 \(i\ge 2\) 则B[i]=b[i-1]+A[i]。参考代码
#include<bits/stdc++.h> using namespace std; const int N=1e5+10; int n,a[N],b[N]; int main() { cin >> n; for (int i = 1; i <= n; i++) { cin >> a[i]; } // 前缀和数组的第一项和原数组的第一项是相等的。 b[1] = a[1]; for (int i = 2; i <= n; i++) { // 前缀和数组的第 i 项 = 原数组的 0 到 i-1 项的和 + 原数组的第 i 项。 b[i] = b[i - 1] + a[i]; } for (int i = 1; i <= n; i++) { cout << b[i] << " "; } return 0; }
二维/多维前缀和
常见的多维前缀和的求解方法有两种。
-
基于容斥原理
这种方法多用于二维前缀和的情形。给定大小为 \(m\times n\) 的二维数组 \(a\),要求出其前缀和 \(s\)。那么,\(s\) 同样是大小为 \(m\times n\) 的二维数组,且
\[s_{i,j}\gets\begin{aligned} \sum_{i'\leq i}\end{aligned}\begin{aligned} \sum_{j'\leq j}\end{aligned}A_{i',j'} \]类比一维的情形,\(s_{i,j}\) 应该可以基于 \(s_{i-1,j}\) 或 \(s_{i,j-1}\) 计算,从而避免重复计算前面若干项的和。但是,如果直接将 \(s_{i-1,j}\) 和 \(s_{i,j-1}\) 相加,再加上 \(a_{i,j}\),会导致重复计算 \(s_{i-1,j-1}\) 这一重叠部分的前缀和,所以还需要再讲这部分减掉。这就是 容斥原理。由此得到如下递推关系:
\[s_{i,j}=a_{i,j}+s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1} \]实现是,直接遍历 \((i,j)\) 求和即可。
有
\[s_{3,3}=a_{3,3}+s_{2,3}+s_{3,2}-s_{2,2}=5+18+15-9=29 \]可以在 \(O(1)\) 时间内完成。
-
逐维前缀和
对于一般的情形,给定 \(k\) 维数组 \(a\),大小为 \(n\),同样要求得其前缀和 \(s\)。这里,
\[s_{i_1,\cdots,i_k}=\begin{aligned} \sum_{i'_1\le i_1}\end{aligned}\cdots\begin{aligned} \sum_{i'_k\le i_k}\end{aligned}a_{i'_1,\cdots,i'_k} \]从上式可以看出,\(k\) 维前缀和就等于 \(k\) 次求和。所以,一个显然的算法是,每次只考虑一个维度,固定所有其它维度,然后求若干个一维前缀和,这样对所有 \(k\) 个维度分别求和之后,得到的就是 \(k\) 维前缀和。
提供一个3维的高维前缀和参考代码:
int a[n+1][n+1][n+1],b[1<<n]; int fun(int i,int j,int k){ return i*4+j*2+k; } int main(){ //高维前缀和 for(int i=2;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) a[i][j][k]+=a[i-1][j][k]; for(int i=1;i<=n;i++) for(int j=2;j<=n;j++) for(int k=1;k<=n;k++) a[i][j][k]+=a[i][j-1][k]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=2;k<=n;k++) a[i][j][k]+=a[i][j][k-1]; //等价于 for(int i=2;i<=n;i++) for(int j=1;j<=n;j++) for(int k=1;k<=n;k++) b[fun(i,j,k)]+=b[fun(i-1,j,k)]; for(int i=1;i<=n;i++) for(int j=2;j<=n;j++) for(int k=1;k<=n;k++) b[fun(i,j,k)]+=b[fun(i,j-1,k)]; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) for(int k=2;k<=n;k++) b[fun(i,j,k)]+=b[fun(i,j-1,k)]; //等价于 for(int h=1<<(n-1);h>0;h>>=1) for(int i=0;i<1<<n;i++) if(i&h) b[i]+=b[i-h]; return 0; }因为考虑每一个维度的时候,都只遍历了整个数组一遍,这样的算法复杂度是 \(O(k\cdot N)\) 的,通常可以接受。
树上前缀和
设 \(sum_i\) 表示结点 \(i\) 到根节点的权值总和。
然后:
- 若是点权,\(x,y\) 路径上的和为 \(sum_x+sum_y-sum_{lca}-sum_{fa_{lca}}\)。
- 若是边权,\(x,y\) 路径上的和为 \(sum_x+sum_y-2\cdot sum_{lca}\)。
\(\operatorname{LCA}\) 的求法参见 最近公共祖先。
差分
解释
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
这种策略的定义是令 \(b_i = \begin{cases} a_i - a_{i-1} & i \in [2,n] \\ a_1 & i=1 \end{cases}\)
性质
- \(a_i\) 的值是 \(b_i\) 的前缀和,即 \(a_n = \begin{aligned} \sum_{i=1}^n\end{aligned}b_i\)
- 计算 \(a_i\) 的前缀和 $sum = \begin{aligned} \sum_{i=1}^n\end{aligned}a_i=\begin{aligned} \sum_{i=1}^n\end{aligned}\begin{aligned} \sum_{j=1}^i\end{aligned}b_j=\begin{aligned} \sum_{i=1}^n\end{aligned}(b-i+1)b_i $
它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。
树上差分
树上差分可以理解为对树上的某一段路径进行差分操作,这里的路径可以类比一维数组的区间进行理解。例如在对树上的一些路径进行频繁操作,并且询问某条边或者某个点在经过操作后的值的时候,就可以运用树上差分思想了。
树上差分通常会结合 最近公共祖先 来进行考察。树上差分又分为 点差分 与 边差分,在实现上会稍有不同。
点差分
举例:对树上的一些路径 \(\delta(s_1,t_1), \delta(s_2,t_2), \delta(s_3,t_3)\dots\) 进行访问,问一条路径 \(\delta(s,t)\) 上的点被访问的次数。
对于一次 \(\delta(s,t)\) 的访问,需要找到 \(s\) 与 \(t\) 的公共祖先,然后对这条路径上的点进行访问(点的权值加 \(1\)),若采用 DFS 算法对每个点进行访问,由于有太多的路径需要访问,时间上承受不了。这里进行差分操作:
其中 \(father(x)\) 表示 \(x\) 的父亲结点,\(d_i\) 为点权 \(a_i\) 的差分数组。
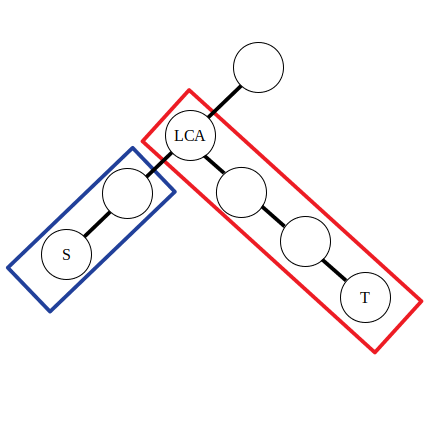
可以认为公式中的前两条是对蓝色方框内的路径进行操作,后两条是对红色方框内的路径进行操作。不妨令 \(\textit{lca}\) 左侧的直系子节点为 \(\textit{left}\)。那么有 \(d_{\textit{lca}}-1=a_{\textit{lca}}-(a_{\textit{left}}+1),d_{f(\textit{lca})}-1=a_{f(\textit{lca})}-(a_{\textit{lca}}+1)\)。可以发现实际上点差分的操作和上文一维数组的差分操作是类似的。
边差分
若是对路径中的边进行访问,就需要采用边差分策略了,使用以下公式:
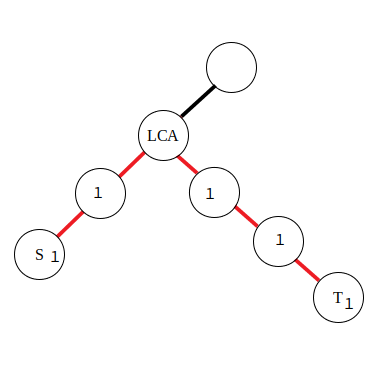
由于在边上直接进行差分比较困难,所以将本来应当累加到红色边上的值向下移动到附近的点里,那么操作起来也就方便了。对于公式,有了点差分的理解基础后也不难推导,同样是对两段区间进行差分。
例题
解题思路
需要统计每个点经过了多少次,那么就用树上差分将每一次的路径上的点加一,可以很快得到每个点经过的次数。这里采用倍增法计算 LCA,最后对 DFS 遍历整棵树,在回溯时对差分数组求和就能求得答案了。
参考代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
const int N=5e4+10,L=20;
int n,m,fa[N][L],dep[N],cnt[N],ma,k,pre[N],lg[N];
struct node{
int to;
int next;
}a[2*N];
void add(int u,int v){//建边
a[++k]={v,pre[u]};
pre[u]=k;
return ;
}
void init(){//预处理log2
lg[1]=0;
for(int i=2;i<=n;i++)
lg[i]=lg[i>>1]+1;
return ;
}
void dfs(int x,int fath){//求深度、父亲结点
dep[x]=dep[fath]+1;
fa[x][0]=fath;
for(int i=pre[x];i;i=a[i].next){
int to=a[i].to;
if(to!=fath){
dfs(to,x);
}
}
return ;
}
int lca(int u,int v){//求lca
if(dep[u]<dep[v]) swap(u,v);
while(dep[u]!=dep[v]){
u=fa[u][lg[dep[u]-dep[v]]];
}
if(u==v) return u;
for(int i=L-1;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
u=fa[u][i];
v=fa[v][i];
}
}
return fa[u][0];
}
void dfs2(int x,int fath){
for(int i=pre[x];i;i=a[i].next){
int to=a[i].to;
if(to!=fath){
dfs2(to,x);
cnt[x]+=cnt[to];//差分后前缀和操作
}
}
ma=max(ma,cnt[x]);
return ;
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1,x,y;i<n;i++){
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
init();
dfs(1,0);
//倍增法求lca
for(int j=1;j<L;j++){
for(int i=1;i<=n;i++){
fa[i][j]=fa[fa[i][j-1]][j-1];
}
}
for(int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
int lc=lca(x,y);
//差分
cnt[x]++;
cnt[y]++;
cnt[lc]--;
cnt[fa[lc][0]]--;
}
dfs2(1,0);
printf("%d",ma);
return 0;
}
部分图片与文献来自oi-wiki。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号