[题解] 洛谷 P8479 「GLR-R3」谷雨 题解
防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透防剧透阅读全文
第一次写黑题题解,特别纪念一下。
前言
偷偷的说(别被他本人发现了已经被发现了):今年是老师Rainybunny出这道题的第 \(3\) 年,当他给我讲树链剖分的时,语言略带神秘,但不禁露出些许自豪的说,这道题是他出的。
但,即使是他出的,我也要吐槽一下:这什么屎山代码?
有大佬用虚实链剖分切了,鄙人不才,所以写一个大家都可以理解的题解供大家参考。
题目大意
给定 \(n\) 个结点的树,有 \(q\) 次操作,如下:
- 修改:对于在路径 \((u,v)\) 上的节点或在路径上的邻接点 \(x\),将 \(x\) 的点权变为 \(k\)。
- 查询:对于在路径 \((u,v)\) 上的节点 \(x\):
1.将 \(x\) 的点权加入 \(S\);
2.按标号升序枚举 \(x\) 的不在路径上的邻接点 \(y\),将 \(y\) 的点权加入 \(S\)。求 \(S\) 的最大可空子段和。
看似很简单。
引入
大家都知道「NOI 2021」轻重边这道题吧,这道题是这样的:
每条边一开始都是轻边。
有两种操作:
- 修改:将 \((u,v)\) 路径上的点的邻接点变成轻边,再将 \((u,v)\) 路径上的边变成重边。
- 查询:\((u,v)\) 上一共有多少条重边。
我们发现了一个没有什么用的性质:每次修改的部分很像一条毛毛虫。
显然,我们要将边变成点,用一个点表示一条边,可以说这样做是很疯狂的,非常恐怖。
不妨换一个思路,一条边是重边,当且仅当:它被次修改的路径包含,并且在此次修改后, 它的两个端点都没有被其他修改路径包含。
换句话说:最后一次涉及这条边的两个端点的修改是同一个修改。
如此,我们便解决了这道题,但是,对毛毛虫的修改和对路径查询,真的不能做吗?
答案是:能!
思路
回忆树链剖分的基本逻辑:将需要维护的信息(树上路径)通过重编号(dfn)实现到区间上。现在,我们更关心所谓的毛毛虫的信息,那么就需要设计一种将毛毛虫通过重编号转化到区间的算法。
我们先定义一下毛毛虫的结构:对于数 \(Tree=(V,E)\) 和树上一条路径的点集 \(P\),定义毛毛虫为:
同时,我们亲切的称 \(P\) 为 \(C\) 的毛毛虫虫身,\(C\setminus P\) 为 \(C\) 的虫足。
这样,原题的两种操作可以用一下三种操作组合而成:
- 虫足点权赋值(为 \(0\),除了 \(LCA\) 的父亲);
- 虫身赋值(为 \(1\),除了 \(LCA\));
- 虫身点权和查询(减去 \(LCA\) 贡献)。
重点:解决了定义,但如何剖分?
汪老师在课堂上说这个是毛毛虫剖分。
首先,为什么我们要用重链?因为我们跳整个链,从 \(S_u\gets2S_u\),我们只有用重链剖分才能保证我的时间复杂度。
但是,我们要再重链剖分的基础上改进一下,在其原有的性质的基础上增加必要的性质。
对于本题来说,重编号方法不难构造。先为树根编号,接着从树根所在的重链出发,依次进行:
- 为除重链头 \(top\) 以外的重链结点依次编号;
- 依次枚举重链结点,为它们的轻儿子依次编号(这些儿子是其他重链的 \(top\));
- 任意顺序递归 \(2.\) 中的轻儿子。
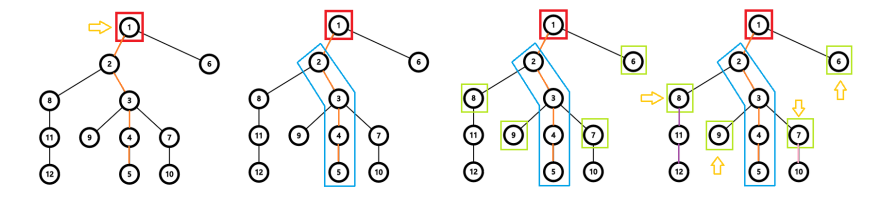
在这幅图中,黄色箭头表示将要递归的子树;橙色边是重边;蓝色的框是重儿子;绿色框是重链两边的轻儿子。
可以看出,毛毛虫剖分的重编号的性质:
- 对于重链,除 \(top\) 外的结点编号连续;
- 对于任意结点,其轻儿子编号连续;
- 对于重链毛毛虫,除 \(top\) 的父亲外所有虫足编号连续。
所以,毛毛虫剖分可以很方便的维护毛毛虫信息。并且,他能顺便维护重链剖分的所有信息,还能维护子树的所有信息(子树最多剖分为三部分:重链区间、邻接轻点区间、邻接轻子树区间)。
时间复杂度为:\(O(q\log^2n)\),与重链剖分完全一样。
屎山代码
知道了思路就很好做了,但是写的时候很难说。
#include <bits/stdc++.h>
#define For(i, l, r) for (int i = l;i <= r; i++)
#define min(a,b) (a)<(b)?(a):(b)
#define max(a,b) (a)<(b)?(b):(a)
#define LL long long
#define fi first
#define se second
using namespace std;
inline int read() {
int x;
cin >> x;
return x;
}
const int N = 1e5 + 10, IINF = 0x3f3f3f3f;
int n, ecnt, fa[N], val[N], head[N];
int dep[N], siz[N], son[N];
vector<int> g[N];
int dfc[2], dfn[N][2], top[N], rnk[N][2];
int clef[N][2], crig[N][2];
int spos[N][2];
struct Atom {
LL sum, lmx, rmx, amx;
inline Atom rev() const {
return { sum, rmx, lmx, amx };
}
inline Atom operator + (const Atom& t) const {
return {sum + t.sum, max(lmx, sum + t.lmx), max(rmx + t.sum, t.rmx), max(max(amx, t.amx), rmx + t.lmx)};
}
inline Atom& operator *= (const Atom& t) {
return *this = *this + t;
}
inline Atom& operator += (const Atom& t) {
return *this = t + *this;
}
};
struct SegmentTree {//学会封装线段树是很重要的
Atom uni[N << 2];
int len[N << 2], tag[N << 2];
inline void pushup(const int u) {
uni[u] = uni[u << 1] + uni[u << 1 | 1];
}
inline void build(int u, int l, int r, int id) {
len[u] = r - l + 1, tag[u] = IINF;
if (l == r) {
uni[u].sum = val[rnk[l][id]];
uni[u].lmx = uni[u].rmx = uni[u].amx = max(0, val[rnk[l][id]]);
return ;
}
int mid = (l + r) >> 1;
build(u << 1, l, mid, id), build(u << 1 | 1, mid + 1, r, id);
pushup(u);
}
inline void change(int u, int v) {
tag[u] = v, uni[u].sum = 1ll * len[u] * v;
uni[u].lmx = uni[u].rmx = uni[u].amx = max(0ll, uni[u].sum);
}
inline void pushdown(int u) {
if (tag[u] != IINF) {
change(u << 1, tag[u]), change(u << 1 | 1, tag[u]);
tag[u] = IINF;
}
}
inline void mulity(int u, int l, int r,int al, int ar, int k) {
if (al > ar) return ;
if (al <= l && r <= ar) return change(u, k);
int mid = (l + r) >> 1;
pushdown(u);
if (al <= mid) mulity(u << 1, l, mid, al, ar, k);
if (mid < ar) mulity(u << 1 | 1, mid + 1, r, al, ar, k);
pushup(u);
}
inline Atom query(int u, int l, int r,int ql, int qr) {
if (ql > qr) return { 0, 0, 0, 0 };
if (ql <= l && r <= qr) return uni[u];
int mid = (l + r) >> 1;
pushdown(u);
if (qr <= mid) return query(u << 1, l, mid, ql, qr);
if (mid < ql) return query(u << 1 | 1, mid + 1, r, ql, qr);
return query(u << 1, l, mid, ql, qr)
+ query(u << 1 | 1, mid + 1, r, ql, qr);
}
} T[2];
inline void dfs1(int u) {
siz[u] = 1, dep[u] = dep[fa[u]] + 1;
for (int v : g[u]) {
dfs1(v), siz[u] += siz[v];
if (siz[v] > siz[son[u]]) son[u] = v;
}
}
inline void retopF(int u) {
clef[u][0] = dfc[0] + 1;
if (!top[u]) dfn[u][0] = ++dfc[0];
for (int v : g[u]) {
if (v == son[u]) spos[u][0] = dfc[0];
else dfn[v][0] = ++dfc[0];
}
crig[u][0] = dfc[0];
if (son[u]) retopF(son[u]);
}
inline void retopR(int u) {
clef[u][1] = dfc[1] + 1;
for (int i = int(g[u].size()) - 1, v; ~i; --i) {
if ((v = g[u][i]) == son[u]) spos[u][1] = dfc[1];
else dfn[v][1] = ++dfc[1];
}
if (!top[u]) dfn[u][1] = ++dfc[1];
crig[u][1] = dfc[1];
if (son[u]) retopR(son[u]);
}
inline void dfs2(int u, int tp) {
top[u] = tp;
if (u == tp) retopF(u), retopR(u);
if (son[u]) dfs2(son[u], tp);
for (int v : g[u]) if (v != son[u]) dfs2(v, v);
}
inline int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) v = fa[top[v]];
else u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
inline void mulity(int u, int v, int k, int id) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) u ^= v ^= u ^= v;
T[id].mulity(1, 1, n, clef[top[u]][id], crig[u][id], k);
if (son[u]) {
T[id].mulity(1, 1, n, dfn[son[u]][id], dfn[son[u]][id], k);
}
u = top[u];
T[id].mulity(1, 1, n, dfn[u][id], dfn[u][id], k);
u = fa[u];
}
if (dep[u] < dep[v]) u ^= v ^= u ^= v;
T[id].mulity(1, 1, n, clef[v][id], crig[u][id], k);
if (son[u]) T[id].mulity(1, 1, n, dfn[son[u]][id], dfn[son[u]][id], k);
if (v == top[v]) T[id].mulity(1, 1, n, dfn[v][id], dfn[v][id], k);
if (fa[v]) T[id].mulity(1, 1, n, dfn[fa[v]][id], dfn[fa[v]][id], k);
}
inline void append(Atom& res, int u, int p,int id) {
int l = clef[u][id];
if (dfn[p][id] < spos[u][id]) {
res += T[id].query(1, 1, n, spos[u][id] + 1, crig[u][id]);
res += T[id].query(1, 1, n, dfn[son[u]][id], dfn[son[u]][id]);
res += T[id].query(1, 1, n, max(dfn[p][id] + 1, l), spos[u][id]);
res += T[id].query(1, 1, n, l, dfn[p][id] - 1);
} else {
res += T[id].query(1, 1, n, max(dfn[p][id] + 1, l), crig[u][id]);
res += T[id].query(1, 1, n, max(spos[u][id] + 1, l), dfn[p][id] - 1);
if (son[u])
res += T[id].query(1, 1, n, dfn[son[u]][id], dfn[son[u]][id]);
res += T[id].query(1, 1, n, l, min(spos[u][id], dfn[p][id] - 1));
}
}
inline pair<Atom, int> climb(int u, int tar, int id) {
Atom ret = { 0, 0, 0, 0 };
int p = 0;
while (top[u] != top[tar]) {
if (u != top[u]) {
append(ret, u, p, id);
ret += T[id].query(1, 1, n,
crig[top[u]][id] + 1, clef[u][id] - 1);
u = top[u];
if (!id) {
ret += T[0].query(1, 1, n, clef[u][0], crig[u][0]);
ret += T[0].query(1, 1, n, dfn[u][0], dfn[u][0]);
} else {
ret += T[1].query(1, 1, n, dfn[u][1], dfn[u][1]);
ret += T[1].query(1, 1, n, clef[u][1], crig[u][1]);
}
} else if (!id) {
append(ret, u, p, 0);
ret += T[0].query(1, 1, n, dfn[u][0], dfn[u][0]);
} else {
ret += T[1].query(1, 1, n, dfn[u][1], dfn[u][1]);
append(ret, u, p, 1);
}
u = fa[p = u];
}
if (u != tar) {
append(ret, u, p, id);
ret += T[id].query(1, 1, n, clef[p = son[tar]][id], clef[u][id] - 1);
}
return { ret, p };
}
inline LL query(int u, int v) {
int w = lca(u, v);
auto su(climb(u, w, 1)), sv(climb(v, w, 0));
auto ret(su.fi.rev());
ret *= T[0].query(1, 1, n, dfn[w][0], dfn[w][0]);
if (fa[w]) ret *= T[0].query(1, 1, n, dfn[fa[w]][0], dfn[fa[w]][0]);
vector<pair<int, int> > tmp;
if (su.se && su.se != son[w]) tmp.push_back({ dfn[su.se][0], 0 });
if (sv.se && sv.se != son[w]) tmp.push_back({ dfn[sv.se][0], 0 });
if (su.se != son[w] && sv.se != son[w]) tmp.push_back({ spos[w][0], 2 });
tmp.push_back({ crig[w][0], 1 });
sort(tmp.begin(), tmp.end());
int las = clef[w][0] + (w != top[w]);
for (auto& p : tmp) {
ret *= T[0].query(1, 1, n, las, p.fi - !p.se);
if (p.fi == spos[w][0] && p.se == 2) {
ret = ret + T[0].query(1, 1, n, dfn[son[w]][0], dfn[son[w]][0]);
}
las = p.fi + 1;
}
ret *= sv.fi;
return ret.amx;
}
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
read(), n = read();
For (i, 1, n) val[i] = read();
For (i, 2, n) g[fa[i] = read()].push_back(i);
dfs1(1);
dfn[1][0] = dfc[0] = dfn[1][1] = dfc[1] = 1;
dfs2(1, 1);
For (i, 1, n) rnk[dfn[i][0]][0] = rnk[dfn[i][1]][1] = i;
T[0].build(1, 1, n, 0), T[1].build(1, 1, n, 1);
for (int q = read(), op, u, v, k; q--;) {
op = read(), u = read(), v = read();
if (!op) k = read(), mulity(u, v, k, 0), mulity(u, v, k, 1);
else cout << query(u, v) << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号