7.23小测
预计估分:\(100+100+100+50=350\)。
实际得分:\(100+100+100+50=350\)。Rank.3。
被 pyh,yjl 俩大佬爆杀了。
(最大公约数)I. 妙妙咒语
I.I 题意
有 \(n(2\le n\le500)\) 个点,编号为 \(1\sim n\),第 \(i\) 个点位于 \(x_i,y_i(0\le x_i,y_i\le10^9)\),且所有点的坐标不同。
kkkw 可以用咒语来在点之间传送。对于每种咒语由 \((a,b)\) 标识,对坐标 \((x,y)\) 施放咒语 \((a,b)\) 会将你传送到 \((x+a,y+b)\)。咒语可以使用多次。
kkkw会所有咒语,但是请问他只需要用到多少咒语,即可实现在点之中自由穿梭呢?
I.II 题解
I.III 代码
/*+ Cloudybunny +*/
#include<bits/stdc++.h>
#define endl '\n'
#define pi pair<int,int>
using namespace std;
const int INF=INT_MAX;
const int mod=1e9+7;
const int N=2e5+10;
pi a[N];
set<pi> s;
int gcd(int a,int b){
return (b?gcd(b,a%b):a);
}
signed main(){
cin.tie(0)->sync_with_stdio(false);
int n;
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i].first>>a[i].second;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
int dx=a[j].first-a[i].first,dy=a[j].second-a[i].second;
int g=gcd(dx,dy);
if(g!=0) dx/=g,dy/=g;
if(dx<0||(dx==0&&dy<0)) dx=-dx,dy=-dy;
s.insert({dx,dy});
}
}
cout<<s.size()*2;
return 0;
}
(二分)II. 木雕玩具
II.I 题意
有 \(n\) 个图案用 \(a_i\) 表示。共 \(3\) 个雕刻师,每个雕刻师选择一个 \(x\) 图案,钦定一个图案 \(y\),所用的时间是 \(\mid x-y\mid\)。
请问 \(3\) 个雕刻师雕刻完 \(n\) 个图案,雕刻时间最长的图案最短要多长时间?
II.II 题解
不妨设 \(a\) 单调递增(无重复),显然如果 \(n\le3\),答案就是 \(0\)>
显然答案 \(k\) 具有可二分性。也就是说,当 \(k\le k_0\) 时一定不存在合法的 \(x,y,z\),当 \(k\le k_0\) 时一定存在,\(k_0\) 就是答案。
因此二分答案,只需要验证答案 \(k\) 是否存在合法的 \(x,y,z\)。
为了覆盖到 \(a_1\),且 \(x\) 尽量往大取(这样可以覆盖更多的 \(a_i\)),我们令 \(x=a_1+k\)。接下来一段区间的 \(a_i\) 会被 \([x-k,x+k]\) 覆盖,我们跳过这段区间,找到下一个未被覆盖的 \(a_i\)。类似于刚刚的思路,我们令 \(y=a_i+k\),再找到下一个未被覆盖的 \(a_j\),令 \(z=a_j+k\)。如果此时所有 \(a_i\) 都被覆盖了,那么就合法,否则不合法。
时间复杂度 \(\mathcal{O}(n\log w)\),其中 \(w\) 为值域。
II.III 代码
/*+ Cloudybunny +*/
#include<bits/stdc++.h>
#define endl '\n'
#define pi pair<int,int>
using namespace std;
const int INF = INT_MAX;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int n, a[N];
inline int read(){
int x;
cin >> x;
return x;
}
inline bool check(int mid){
int x = upper_bound(a + 1, a + n + 1, a[1] + mid * 2) - a;
if (x > n) return true;
int y = upper_bound(a + 1, a + n + 1, a[x] + mid * 2) - a;
if (y > n) return true;
int z = upper_bound(a + 1, a + n + 1, a[y] + mid * 2) - a;
if (z > n) return true;
return false;
}
signed main(){
cin.tie(0)->sync_with_stdio(false);
n = read();
if (n <= 3) return cout << 0 << endl, 0;
for (int i = 1; i <= n; i++) a[i] = read();
sort(a + 1, a + n + 1);
int l = 0, r = 1e9, ans = -1;
while (l <= r){
int mid =(l + r) >> 1;
if (check(mid)) r = mid - 1, ans = mid;
else l = mid + 1;
}
cout << ans << endl;
return 0;
}
(割点思想)III. 枢纽
前置:割点。
III.I 题意
有 \(n\) 个点,\(m\)条边,有 \(u\) 和 \(v\) 两个重要节点。问有多少对 \((a,b)\) 满足:
- \(1\le u<v\le n\)。
- \(u\ne a,v\ne a,u\ne b,v\ne b\)。
- 任意一条从 \(u\) 到 \(v\) 的路径都经过 \(a,b\)。
III.II 题解
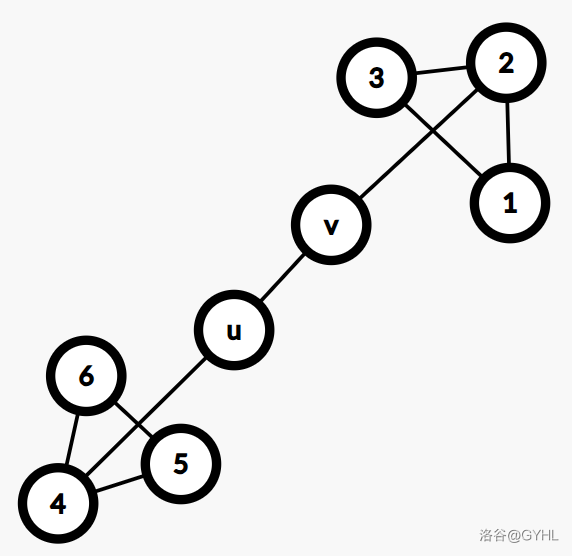
从“任意一条从 \(u\) 到 \(v\) 的路径都经过 \(a,b\)。”,可以说,\(u,v\) 是割点了。
只有这种情况才能使答案大于 \(0\),不然所有的 \((a,b)\) 的所有路径不可能都经过 \(u\) 和 \(v\)。
所以,判断 \(u\) 和 \(v\) 各自的集合的点的数量,相乘即可。
III.III 代码
/*+ Cloudybunny +*/
#include<bits/stdc++.h>
#define endl '\n'
#define pi pair<int,int>
#define int long long
using namespace std;
const int INF=INT_MAX;
const int mod=1e9+7;
const int N=2e5+10,M=5e5+10;
int n,m,s1,s2,d[N];
bool f[N];
int pre[N],k;
struct node{
int to,next;
}a[M<<1];
inline void add(int u,int v){
a[++k]={v,pre[u]};
pre[u]=k;
return ;
}
void dfs1(int x,int fath){
for(int i=pre[x];i;i=a[i].next){
int to=a[i].to;
if(fath==to) continue;
if(f[to]) continue;
if(to==s2) return ;
d[to]++;
f[to]=true;
dfs1(to,x);
}
return ;
}
void dfs2(int x,int fath){
for(int i=pre[x];i;i=a[i].next){
int to=a[i].to;
if(fath==to) continue;
if(f[to]) continue;
if(to==s1) return ;
d[to]+=2;
f[to]=true;
dfs2(to,x);
}
return ;
}
inline int read(){
int x;
cin>>x;
return x;
}
signed main(){
cin.tie(0)->sync_with_stdio(false);
cin>>n>>m>>s1>>s2;
for(int i=1;i<=m;i++){
int u=read(),v=read();
add(u,v);
add(v,u);
}
dfs1(s1,0);
memset(f,false,sizeof f);
dfs2(s2,0);
// for(int i=1;i<=n;i++) cout<<d[i]<<" ";
int ans1=0,ans2=0;
for(int i=1;i<=n;i++){
if(i==s1||i==s2) continue;
if(d[i]==1) ans1++;
if(d[i]==2) ans2++;
}
cout<<ans1*ans2<<endl;
return 0;
}
(dp)IV. 魔法药水
IV.I 题意
现在有 \(n\) 种材料,第 \(i\) 种材料的魔力为 \(a_i\)。
你要从这些材料中选择一种或多种混合,制作一种药水,混合 \(k\) 种材料时,药水每单位时间的魔力会增加 \(k\)。药水的初始魔力值等于所选材料的魔力和。
你会在 \(0\) 时刻把所有材料一次性混合好,而之后不会再添加材料。
你想知道,最早在第几时刻,药水魔力值能正好达到 \(m\)?
IV.II 题解
IV.II.I 问题重述
我们需要从给定的材料中选择 \(s\) 个材料,使得这些材料的魔力之和 \(sum\) 满足:
目标是让达到 \(m\) 的时间尽可能短。时间可以表示为:
为了最小化时间,在固定 \(s\) 的情况下,如果有多个方案满足条件,应选择 \(sum\) 最大的那个,因为这样会使 \(\frac{m-sum}{s}\) 最小。
IV.II.II 动态规划思路
为了找到最优解,可以使用动态规划(DP)的方法。定义状态 \(f_{i,j,k}\) 如下:
- \(i\):考虑前 \(i\) 种材料。
- \(j\):已经选择了 \(j\) 个材料。
- \(k\):当前选择的材料的魔力之和 \(sum\) 对 \(s\) 取模的结果。
- \(f_{i,j,k}\):在前 \(i\) 个材料中选择 \(j\) 个材料,使得 \(sum\mod s=k\) 的最大 \(sum\) 值。
IV.II.III 转移方程
对于每个状态 \(f_{i,j,k}\),可以从以下两种情况转移而来:
-
不选第 \(i\) 个材料:直接继承前 \(i-1\) 个材料的状态。
\[f_{i,j,k}=f_{i-1,j,k} \] -
选第 \(i\) 个材料:需要满足已经选了 \(j-1\) 个材料,并且前 \(i-1\) 个材料中选了 \(j-1\) 个材料的某个状态可以转移到当前状态。
- 设第 \(i\) 个材料的魔力值为 \(a_i\)。
- 我们需要找到一个余数 \(k'\) 使得:\[(k'+a_i)\mod s=k \]即:\[k'=(k-a_i)\mod s \]为了保证 \(k'\) 为正,可以写为:
\(k'=(k-a_i\mod s+s)\mod s\) - 因此,转移方程为:
\(f_{i,j,k}=\max(f_{i,j,k},f_{i-1,j-1,k'}+a_i)\)
其中 \(k'=(k-a_i\mod s+s)\mod s\)。
IV.II.IV 初始条件
- \(f_{0,0,0}=0\):表示选了 \(0\) 个材料,余数为 \(0\) 时,\(sum=0\)。
- 其他状态初始化为负无穷(表示不可达)。
IV.II.V 最终答案
对于每个可能的 \(s\)(从 \(1\sim n\)),我们需要检查 \(f_{n,s,m \mod s}\) 是否可达(即不为负无穷)。如果可达,则计算时间:
最终答案是所有可能的 \(s\) 中对应时间的最小值。
IV.II.VI 时间复杂度
- 外层循环枚举 \(s\):\(\mathcal{O}(n)\)。
- DP 状态数为 \(O(n \times s \times s) = \mathcal{O}(n^3)\)(因为 \(s \leq n\))。
- 因此总时间复杂度为 \(\mathcal{O}(n^4)\)。
IV.II.VII伪代码
min_time = infinity
for s in 1 to n:
target_k = m % s
# Initialize DP table
f = array of size (n+1) x (s+1) x s, filled with -infinity
f[0][0][0] = 0
# Fill DP table
for i in 1 to n:
for j in 0 to s:
for k in 0 to s-1:
# Option 1: do not select material i
f[i][j][k] = f[i-1][j][k]
# Option 2: select material i, if j > 0
if j > 0:
a_i = a[i] #魔力值
k_prime = (k - a_i % s + s) % s
if f[i-1][j-1][k_prime] != -infinity:
f[i][j][k] = max(f[i][j][k], f[i-1][j-1][k_prime] + a_i)
# Check if target is reachable
if f[n][s][target_k] != -infinity:
time = (m - f[n][s][target_k]) / s
if time < min_time:
min_time = time
output min_time
IV.II.VIII 注意事项
- 初始条件:确保 \(f_{0,0,0}=0\) 且其他状态初始为不可达。
- 余数处理:计算 \(k'\) 时需要注意负数的情况,因此使用 \((k - a_i \mod s + s)\mod s\)。
- 边界检查:在转移时确保 \(j>0\) 时才尝试选择材料。
- 目标检查:对于每个 \(s\),检查 \(f_{n,s,m\mod s}\) 是否可达。
IV.III 代码


 浙公网安备 33010602011771号
浙公网安备 33010602011771号