题解：P14942 构造题什么的最讨厌了

这边是题目传送门喵！

序：第一次写构造题题解。

---

题意简述

这是题干原话：

给定正整数 \(n,k\)，问是否存在正整数方阵 \(A_n\) 满足如下两个条件：

• 方阵 \(A_n\) 的最大值恰好为 \(k\)，且 \(1\sim k\) 均在 \(A_n\) 中出现过。
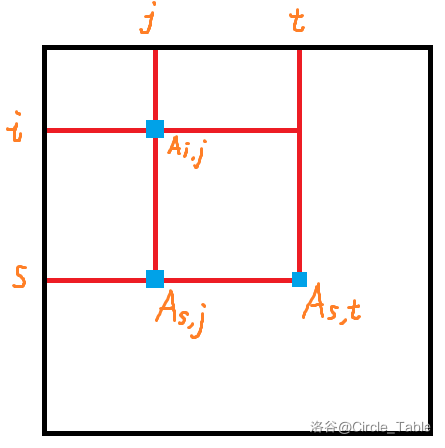
• 不存在整数 \(i,j,s,t\)，其中 \(1\le i<s\le n\) 且 \(1\le j<t\le n\)，满足 \(A_{i,j}=A_{s,j}=A_{s,t}\)。

翻译一下，即不允许出现下图这样的三个点上的数字相等：

思路

第一次写构造题解，也就写详细一点吧。

题目给出了 \(1 \le k \le n^2\) 的数据范围。显然 \(k > n^2\) 时是无解的，因为方阵最多只能容纳 \(1\) 到 \(n^2\) 的所有正整数。

如果 \(k=n^2\) 答案是显而易见的。只需要依次输出即可。

下面考虑更细致的策略。

1. 设 \(k_0\) 是对于 \(n\) 满足存在合法方阵 \(A_n\) 的一个 \(k\)，则对 \(\forall k, k_0 \le k \le n^2\) 都有解。原因很简单，因为达到 \(n^2\) 之前必然存在重复数字，可以用 \(k\) 多余的部分去替换那些重复数字。因此对一个 \(n\) 存在一个最小的 \(k\)，作为有解与无解的分界线。

2. 考虑将 \(k\) 逐渐缩小。第一反应是可以与图的顺序相反地构造。例如 \(n=6\) 时，可按下图方法构造：

    1 1 1 1 1 1
    2 2 2 2 2 1
    3 3 3 3 2 1
    4 4 4 3 2 1
    5 5 4 3 2 1
    6 5 4 3 2 1
   

   这显然是一种合法的构造方式。虽然这并不是最优的，但是足以证明 \(k \ge n\) 时有解。

3. 考虑从其他各种 \(n=k\) 的构造方式中汲取灵感。如果将其斜着投影下来，会发现三个点的投影一定不会在一个点上。

   其实这个很好理解：将原图斜着涂上阴影，每一条阴影的线条都是从右上往左下画。容易看出这三个点一定不会在同一条阴影的线上。

   从而想到这样构造（以 \(n=6\) 为例）：

   1 2 3 4 5 6
   2 3 4 5 6 1
   3 4 5 6 1 2
   4 5 6 1 2 3
   5 6 1 2 3 4
   6 1 2 3 4 5
   

4. 由上一条的启发，既然三个点不会在同一条阴影的线上，那么一定在三条不同的线上。也就是说我们可以将两条线一个数字填充且不会出现连续三条投影线有相同的数字的情况。

   从而想到这样构造（以 \(n=6\) 为例）：

   1 1 2 2 3 3
   1 2 2 3 3 1
   2 2 3 3 1 1
   2 3 3 1 1 2
   3 3 1 1 2 2 
   3 1 1 2 2 3
   

   然而细看发现并不合法。主要问题在于左上角和右下角的两个数字会与其他数字发生神秘反应。要放弃这种方法吗？

5. 回想为什么会出现这两个多出来的数字：是因为奇偶性的原因。

   因此考虑对奇数重新讨论（以 \(n=5\) 为例）：

    1 1 2 2 3
    1 2 2 3 3
    2 2 3 3 1
    2 3 3 1 1
    3 3 1 1 2
   

   发现了一种可行的构造方案。这时 \(k=\lceil \frac{n}{2} \rceil\)。

   细想，如果有 \(k\) 能比这个还小而且还能成立不免太过猎奇了。

   作为题解，考虑证明 \(k \ge \lceil \frac{n}{2} \rceil\) 这个结论。我们考虑反证法，即从 \(k < \lceil \frac{n}{2} \rceil\) 中推出矛盾。又由于开区间不好研究，暂时将目标扩大：证明 \(k > \lfloor \frac{n}{2} \rfloor\)。

   假设存在 \(k\) 使得 \(k \le \lfloor \frac{n}{2} \rfloor\)，则 \(2k \le n\)。

   受到第二条的启发：显然在整个方阵里出现次数最多的的数字的出现次数不超过 \(2n-1\) 次。由第二条的图很容易看出，除了最右上那一圈的 \(1\) 以外的地方，再填任意一个 \(1\) 就会导致题目条件无法满足。

   要用 \(k\) 个数字填满 \(n^2\) 的方阵，就假设每个数字都能用 \(2n-1\) 次，则：

   \[k(2n-1) \ge n^2 \]

   即

   \[-k \ge n^2-2nk \]
   \[k^2 - k \ge (n-k)^2 \ge (n- \lfloor \frac{n}{2} \rfloor)^2 \ge (\frac{n}{2})^2 = \frac{n^2}{4} \]

   这个式子自己看看猎不猎奇。由 \(k \le \lfloor \frac{n}{2} \rfloor,n \ge 1\) 可得：

   \[k^2 - k =(k-\frac{1}{2})^2-\frac{1}{4} < \lfloor \frac{n}{2} \rfloor^2 -\frac{1}{4}<\frac{n^2}{4} \]

   出现矛盾。因此，在最初的假设中，存在 \(k\) 使得 \(k \le \lfloor \frac{n}{2} \rfloor\) 是一个假命题。

   这一段数学证明或许略显复杂（也许这就是文化课带给我的弊病吧），但是得出了一个关键结论：

   \[k > \lfloor \frac{n}{2} \rfloor \]

6. 回到是偶数的情形，既然有 \(k > \lfloor \frac{n}{2} \rfloor\) 这个结论，考虑在 \(n-1\) 的情况最外层加一圈。回到第二点，自然想到了构造方法（以 \(n=6\) 为例）：

   4 4 4 4 4 4
   1 1 2 2 3 4
   1 2 2 3 3 4
   2 2 3 3 1 4
   2 3 3 1 1 4 
   3 3 1 1 2 4
   

   写题解时发现也有很多人的构造方法与我的类似。本篇题解主要写的是我的心路历程，这也启示了构造题从简单的构造开始得到启发来得出正解的一种做法。

代码

#include<bits/stdc++.h>
#define ll long long
#define db double
#define ls u<<1
#define rs u<<1|1
#define pii pair<int,int>
#define fi first
#define se second
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N=25;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int T,a[N][N],f[N][N];
int n,k;

void make(int n,int p){
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            a[i][j]=((i+j)/2-1)%p+1;
        }
    }
    return;
}

void solve(){
    cin>>n>>k;
    int p=n/2+1; // 最小的 k
    if(k<p){ // 无解
        cout<<"fire big\n";
        return;
    }
    if(n%2==1){ // 奇数
        // k=n/2 的构造
        make(n,p);
        // 将剩余的 k 补全
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(k>p){
                    // 第一竖条每个数字的第一次出现，不被替换
                    if(j==1&&i%2==1)f[i][j]=a[i][j];
                    else f[i][j]=k--;
                }
                else f[i][j]=a[i][j];
            }
        }
    }
    else { // 偶数
        // k=n/2+1 的构造
        make(n-1,p-1); // 先构造左下角区域
        for(int j=1;j<=n;j++)f[1][j]=p;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=n-1;j++)f[i][j]=a[i-1][j];
            f[i][n]=p;
        }
        // 将剩余的 k 补全
        for(int i=1;i<=n;i++){
            if(k<=p)break;
            for(int j=1;j<=n;j++){
                if(k>p){
                    // 第一竖条每个数字的第一次出现，不被替换
                    // i!=1:特判最后加进去的一个 p
                    if(i!=1&&j==1&&i%2==0)continue;
                    f[i][j]=k--;
                }
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++)cout<<f[i][j]<<' ';
        cout<<'\n';
    }
    return;
}

int main(){
    ios;cin>>T;
    while(T--)solve();
    return 0;
}

完结撒花！