题解：P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

这边是题目传送门喵！

题意简述

给定 \(n\) 个点，\(m\) 条边的图，求被所有点可达的点的个数。

思路

一、为何 Tarjan

先考虑有向无环图的情形。如果存在明星奶牛，则一定是一个出度为 \(0\) 的点。但是如果超过一个点的出度为 \(0\) 就又会导致不满足条件。因此存在明星奶牛的充要条件是存在且仅存在一个出度为 \(0\) 的点。

放一个图，便于理解。下图的明星奶牛是四号。

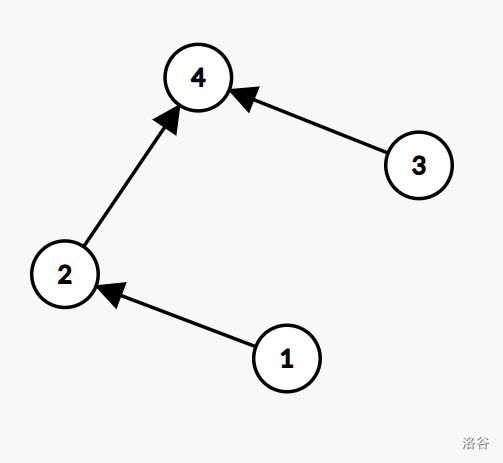
回到原题。但是本题并非有向无环图，而是一个一般图。于是 Tarjan 算法的作用就出现了。

二、何为 Tarjan

Tarjan 算法可以将强联通分量缩成一个点进行考虑。那么对于这个题，可以将原图缩成一个有向无环图，然后找出度为 \(0\) 的点就可以了。

子图：原图的部分点与部分边组成的图。
分量：选取原图中的几个点与这些点之间的所有边组成的子图。
强联通分量：一个分量中的所有点互相可达则称此分量为强联通分量。

三、何以 Tarjan

与 Tarjan 相关重要的变量或数组主要是时间戳 \(dfn\) 和回溯值 \(low\)。

先说这两个值存在的意义：是为了记录我们的缩点是从哪里开始的。其中 \(low\) 比较难以理解，\(low_u\) 可解释为能够到达 \(u\) 的最小时间戳。

每次进入新节点时记录时间戳 \(dfn_u\)，回溯值初始等于时间戳。我们还需要一个栈来记录这个强联通分量中的点数，同时用 \(vis_u\) 来记录这次缩点时 \(u\) 被操作过没有。

在 \(u\) 时遍历与 \(u\) 相连的每一个点 \(v\)，分两种情况处理：

1. 如果 \(v\) 没有被遍历过，那么就将这个点加入强联通分量中，然后回溯值变成 \(\min(low_u,low_v)\)。因为能到达 \(v\) 且 \(u,v\) 同属一个强联通分量，则必然能到达 \(u\)。
2. 如果 \(v\) 没有被遍历过，那么就用 \(v\) 的时间戳 \(dfn_v\) 更新 \(low_u\)。

这一段的代码长这样：

	dfn[u]=low[u]=++tot;
	st.push(u); // 利用一个栈存储强联通分量中的点个数
    vis[u]=1;
	for(auto v:g[u]) {
		if(!dfn[v]) {
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
        else if(vis[v]) {
			low[u]=min(low[u],dfn[v]);
		}
	}

那么，如果是后面遍历到的点，它的回溯值就一定等于靠前的时间戳，则必有 \(dfn_u \not = low_u\)。而对于第一个点，显然其时间戳最小，从而它的回溯值也无法被更新。因此利用 \(dfn_u = low_u\) 来判定一个点是不是开始的第一个点。

然后对于后面的点又全部存储在一个栈中，因此此时将所有栈中节点取出并加入这个强联通分量中。出栈的时候将所有之前遍历是用到了的东西复原。对于任意点 \(u\)，用 \(col_u\) 表示 \(u\) 所在的强联通分量的编号。

	if(dfn[u]==low[u]) {
		color++; // color 代表是第几个强联通分量
        col[u]=color; // col[u] 代表 u 所在强联通分量的编号
        vis[u]=0;
        int v;
		do {
			v=st.top(),st.pop();
			vis[v]=0,col[v]=color;
			siz[color]++;
		} while(u!=v);
	}

然后 Tarjan 就结束了。一会再放 Tarjan 函数的整体代码。那么由上述的过程，我们只要对每一个点跑一次 Tarjan 就可以将每个点都缩进一个强联通分量中了。然而如果之前就被遍历过的点现在不用再跑一次，而之前跑过 Tarjan 就一定会有 \(dfn_u \not = 0\)。

在最后，对每一条边 \(u \rightarrow v\) 考虑，如果 \(u,v\) 在同一个强联通分量内则不用考虑，否则就讲 \(u\) 所在的强联通分量的出度加一，即 \(col_u\) 的出度加一。

利用我们最开始推出的结论，考虑有几个强联通分量出度为 \(0\) 即可知道答案。如果只有一个强联通分量的出度为 \(0\) 则答案为这个强联通分量中的节点个数。

代码：

#include<bits/stdc++.h>
#define ll long long
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N=10005;
int dfn[N],low[N],tot,color,cnt,col[N],siz[N],ans,d[N];
vector<int>g[N];
stack<int>st;
bool vis[N];
int n,m;

void tarjan(int u) {
	dfn[u]=low[u]=++tot;
	st.push(u); // 利用一个栈存储强联通分量中的点个数
    vis[u]=1;
	for(auto v:g[u]) {
		if(!dfn[v]) {
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
        else if(vis[v]) {
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]) {
		color++; // color 代表是第几个强联通分量
        col[u]=color; // col[u] 代表 u 所在强联通分量的编号
        vis[u]=0;
        int v;
		do {
			v=st.top(),st.pop();
			vis[v]=0,col[v]=color;
			siz[color]++; // 记录该强联通分量的节点数
		} while(u!=v);
	}
    return;
}

int main() {
	ios;cin>>n>>m;
	int u,v;
	for(int i=1; i<=m; i++) {
		cin>>u>>v;
		g[u].push_back(v);
	}
	for(int i=1; i<=n; i++) {
		if(!dfn[i]) tarjan(i);
	}
	for(u=1; u<=n; u++) {
		for(auto v:g[u]) {
			if(col[u]==col[v]) continue;
			d[col[u]]++;
		}
	}
	int cnt=0; // 出度为 0 的连通块个数
	for(int i=1; i<=color; i++) if(d[i]==0) cnt++, ans=siz[i];
	if(cnt==1) cout<<ans;
	else cout<<0;
	return 0;
}

完结撒花喵！