题解：P6028 算术

题目传送门

注意到算法标签是整除分块。

\[\begin{align*} f(n) &= \prod^{k}_{i = 1} \frac {p_i^{\alpha_i+1}-1} {p_i ^ { \alpha_i + 1 } - p_i ^ { \alpha_i } } \\ &= \prod^{k}_{i = 1} \frac {(p_i - 1) \displaystyle \sum _ { j = 0 } ^ { \alpha_i} p_i^j } {(p_i-1) p_i^{\alpha_i}} \\ &= \prod^{k}_{i = 1} \frac {\displaystyle \sum _ { j = 0 } ^ { \alpha_i} p_i^j } {p_i^{\alpha_i}} \\ &= \prod^{k}_{i = 1} \displaystyle \sum _ { j = 0 } ^ { \alpha_i} \frac{1}{p_i^j} \\ &= \frac{1}{n} \prod^{k}_{i = 1} \displaystyle \sum _ { j = 0 } ^ { \alpha_i} p_i^j \end{align*} \]

不难发现 \(\frac{1}{n}\) 右边这一块就是 \(n\) 的约数和。

\[f(n) = \frac{\sigma(n)}{n} \]

所求的东西就可以写成这个：

\[\begin{align*} \displaystyle \sum ^n _{i=1} f(i) &= \displaystyle \sum ^n _{i=1} \frac{\sigma(i)}{i} \\ &= \displaystyle \sum ^n _{i=1} \displaystyle \sum _{j|i} \frac{j}{i} \\ &= \displaystyle \sum ^n _{i=1} \displaystyle \sum ^{\lfloor \frac{n}{i} \rfloor}_{j=1} \frac{1}{j} \\ &= \displaystyle \sum ^n _{i=1} \lfloor \frac{n}{i^2} \rfloor \\ &\approx n \displaystyle \sum ^n _{i=1} \frac{1}{i^2} \end{align*} \]

最后一步其实源于我最初写代码的时候打错了但是由于本题的精度限制较低还是可以这么做的。

显然可以对 \(10^6\) 以下的数据直接暴力求出答案。

对于更大的数据我选择通过科技手段找找规律。

如上图是函数 \(g(x)=n\displaystyle \sum ^n _{i=1}\frac{1}{i^2}\) 的图像。将其缩小可以发现：

大致可将其视为线性的。注意到图像在 \((0,+\infty)\) 像是一个正比例函数的图像，因此合理猜测当 \(n\) 足够大时，可将 \(\displaystyle \sum ^n _{i=1}\frac{1}{i^2}\) 视为一个正比例函数的比例系数，也就是说是一个常数。

经历了实践发现还真是。

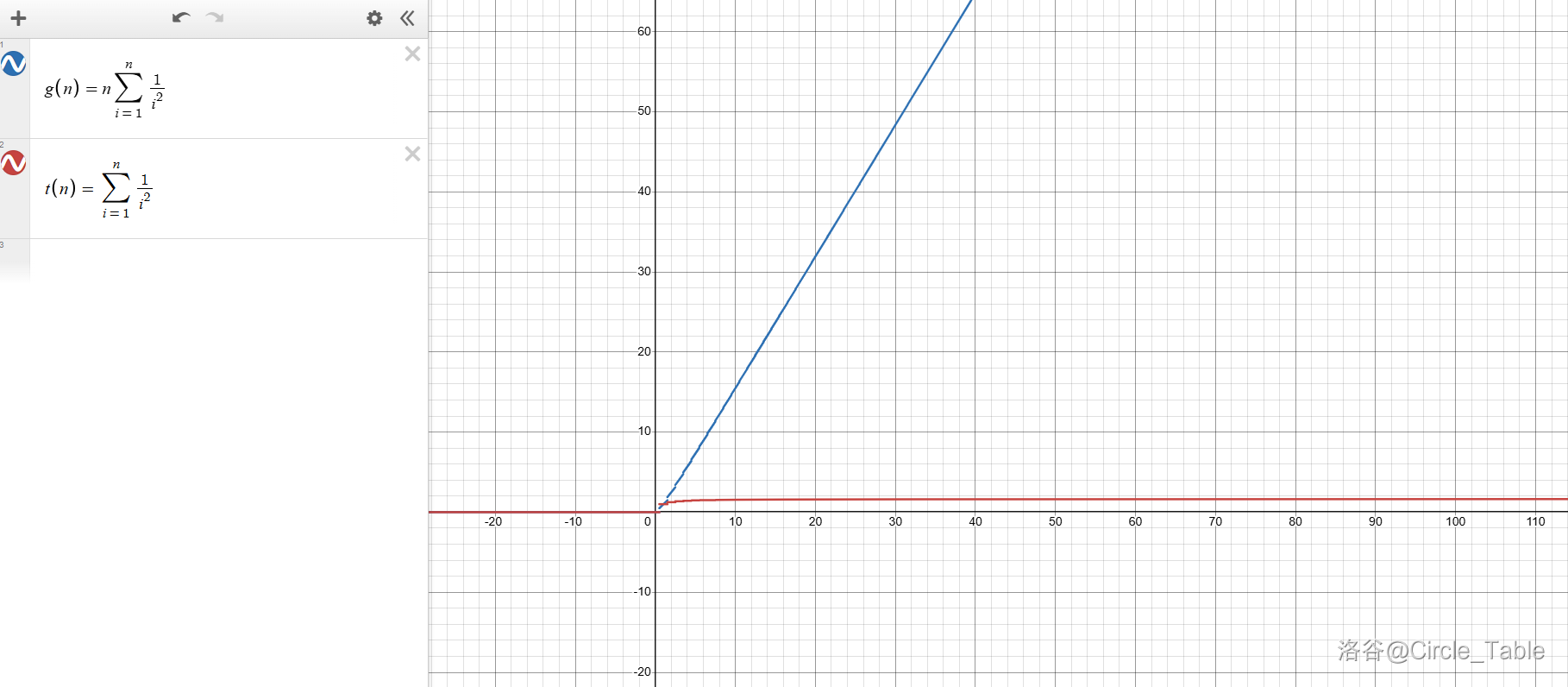
然后估计一下上图红色函数大约是多少。

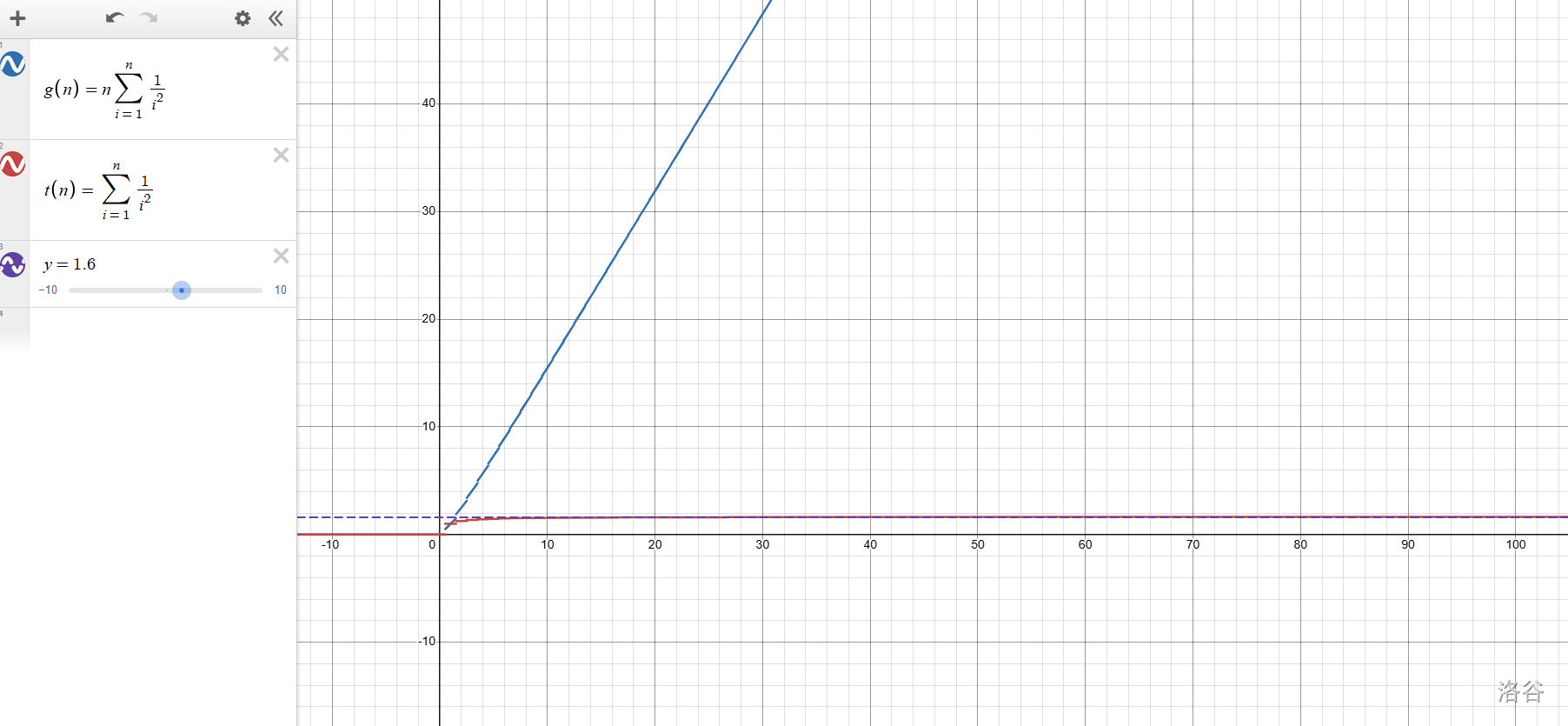
看到紫色的常函数的图像在 \(n\) 逐渐增大时几乎与红色的函数图像重合了。合理猜测 \(\displaystyle \sum ^n _{i=1}\frac{1}{i^2}\) 是一个接近 \(1.6\) 的常数。

因此想到了去求更精确的值，就可以直接通过了。

由上述函数的性质显然可以直接算 \(\displaystyle \sum ^n _{i=1}\frac{1}{i^2}\) 的值。于是取了 \(n=10^{13}\) 挂在机房算了一晚上得出了 \(\displaystyle \sum ^n _{i=1}\frac{1}{i^2} \approx 1.644934066848226436472415049\) 的神秘结果，交了一发直接通过了。

当然如果查阅资料会发现这个值是 \(\zeta(2) = \displaystyle \frac {\pi^2} {6}\) 也可以使用这个，可以发现两者几乎相同。

代码是人都会写。

#include<bits/stdc++.h>
#define ll long long
#define db double
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const ll N=1e6;
const db k=1.644934066848226436472415049;
ll n;
db ans;
int main() {
    ios;
    cin >> n;
    if(n <= N) for(ll i = 1; i <= n; i++) ans += 1.0 * (n/i)/i;
    else ans = k * n - 10;
    cout << fixed << setprecision(10) << ans;
    return 0;
}

完结撒花！