题解：P6175 无向图的最小环问题

题目传送门

题意简述

给定一张无向图，求图中一个至少包含 \(3\) 个点的环，环上的节点不重复，并且环上的边的长度之和最小。

思路

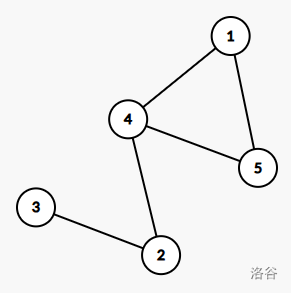
每一个环都可以视为由两点间的一条边与这两点间的路径组成，例如下面这张图，存在唯一的一个环就可以视为 \((1,5)\) 这条边与 \((1,4),(4,5)\) 这条由 \(1\) 到 \(5\) 的路径组成。

因此我们就有完整思路了：

• 在 Floyd 的过程中，刚循环到 \(k,i,j\) 时，更新 \(d (i,j)\) 的前一刻；
• 判断是否 \(i<j<k\) 成立，是就继续，不然普通地更新即可；
• 此时的 \(d_{i,j}\) 根据定义是途径顶点编号都严格小于 \(k\) 的最短路径；
• 如果 \(i,k\) 有连边，\(j,k\) 有连边，即可更新答案。

正确性证明

构成围长的节点中一定有一个编号最大的，当 \(k\) 枚举到它，而 \(i,j\) 枚举到它相邻两个节点时，就成功更新了正确答案。

代码

#include<bits/stdc++.h>
#define ll long long
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
const ll inf=0xffffffff;
//显然将邻接矩阵初始化为 inf 是表示两点没有连边。
const int N=105;
ll n,m,u,v;
ll w,a[N][N],b[N][N],ans=inf;
//a矩阵存储 (i,j) 间的最短路径，b矩阵存储 (i,j) 间直接相连的边

int main()
{
	ios;cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			a[i][j]=b[i][j]=inf;
			//初始化，此时都没有连边。
		}
	}
	for(int i=1;i<=n;i++)
	{
		a[i][i]=b[i][i]=0;
		//自己与自己的连边肯定长度为 0
	}
	for(int i=1;i<=m;i++)
	{
		cin>>u>>v>>w;
		a[u][v]=min(a[u][v],w);
		a[v][u]=min(a[v][u],w);
		b[u][v]=min(b[u][v],w);
		b[v][u]=min(b[v][u],w);
		//这里要注意处理重边
	}
	for(int k=1;k<=n;k++)
	{
		for(int i=1;i<k;i++)
		{
			for(int j=i+1;j<k;j++)
			{
				ans=min(ans,a[i][j]+b[i][k]+b[k][j]);
				//更新答案
			}
		}
		for(int i=1;i<=n;i++)
		{
			for(int j=1;j<=n;j++)
			{
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
				a[j][i]=a[i][j];
				//更新最短路
			}
		}
	}
	if(ans==inf)cout<<"No solution.";//不存在环
	else cout<<ans;
	return 0;
}

总结一下坑点：

1. 此题要开 long long 不然会爆；
2. 记得处理重边，题干中未注明图为简单图；
3. 无解输出包括句号；
4. 调不好的话看看 memset 写对了没有。

完结撒花！