题解：P13291 [GCJ 2013 #1C] Consonants

题目传送门

简单说一下题意：求给定字符串中辅音字母数量不少于 \(n\) 的子串个数。注意是多测。
看完题目后我想都没想就写出了判定辅音的函数。接下来思考提议的实现方法。

现在的题解中似乎没人仔细说明实现的细节，但其实我是想了很久才想出来的。所以来仔细讲讲。

为了表述方便，我们定义最短辅音子串为原字符串中恰有 \(n\) 个辅音字母的子串。
当出现一个最短辅音子串后，那么在它前面的每一个元素到该子串最后一个元素所组成的子串也符合条件。见下图。

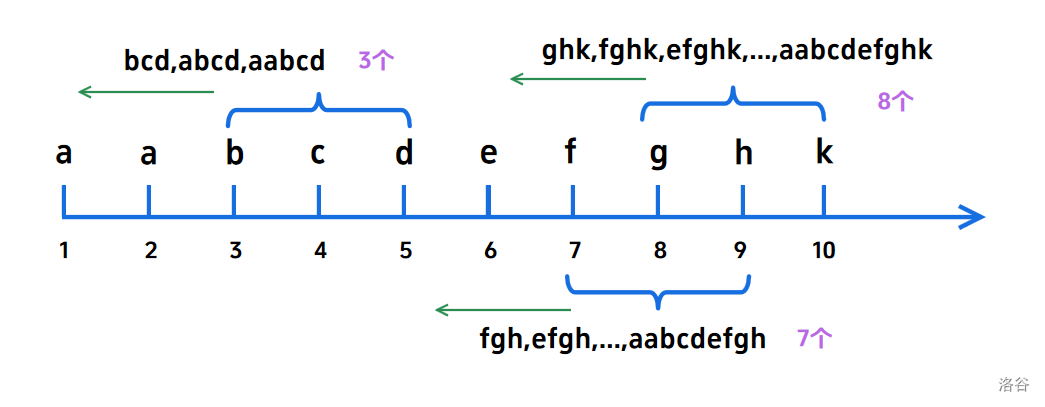
在此图中可以看出，当 \(n=3\) 时，只要满足了连续三个字母是辅音字母，那么这一个子串的左端是几，答案就应该加上几。
这个子串右端为第 \(i\) 个，因此左端的左边一个为第 \(i-n\) 个，左端就是 \(l=i-n+1\) 了。

但是我们仅仅考虑向左。向右的话，还是上图，当我们遍历到 \(i=6\) 时，再往左边看，实际上就是在原先的最短辅音子串的右边加上一个字母罢了。因此再加上一个 \(i-n+1\) 即可。
证明这种计算方法能够做到不重不漏。首先，由于每一个点都只向左寻找符合条件的子串，所以每到一个新点得到的子串就全部不同，因此做到了不重；而根据排列组合，我们确实考虑到了每一个可能的子串，不可能遗漏。

想清楚这些此题答案也就呼之欲出了。其他小细节见注释。

代码如下：

#include<bits/stdc++.h>
#define ll long long
#define ri register int
#define ios ios::sync_with_stdio,cin.tie(0),cout.tie(0)
using namespace std;
const int N=1e6+5;
const char ch[5]={'a','e','i','o','u'};
char s[N];
int T,n,sum[N];
bool isfuyin(char c)//判断辅音的函数 
{
	for(ri i=0;i<5;i++)
		if(c==ch[i])return 0;
	return 1;
}
signed main()
{
	scanf("%d",&T);
	for(ri qwq=1;qwq<=T;qwq++)
	{
		scanf("%s %d",s+1,&n);
		memset(sum,0,sizeof(sum));//多测清空
		int len=strlen(s+1);
		ll ans=0,ans1=0;
		
		//预处理前缀和：求截止到a[i]连续有几个辅音字母
		for(ri i=1;i<=len;i++)
			if(isfuyin(s[i]))sum[i]=sum[i-1]+1;
			//否则sum[i]=0 (见前文memset)
		
		//求值 
		for(ri i=n;i<=len;i++)//从n开始：n以前绝不会有满n个的子串 
		{
			if(sum[i]>=n)ans1=i-n+1;
			ans+=ans1;
		}
		printf("Case #%d: %lld\n",qwq,ans);
	}
	return 0;
}

感谢阅读！