题解：P11752 [COCI 2024/2025 #5] 挂画 / Zid

题目传送门

看到这题的第一想法是用前缀和。用数组 \(a\) 记录 \(a[i][j]\)左上方的钉子数量之和，先抽象出以下图形：

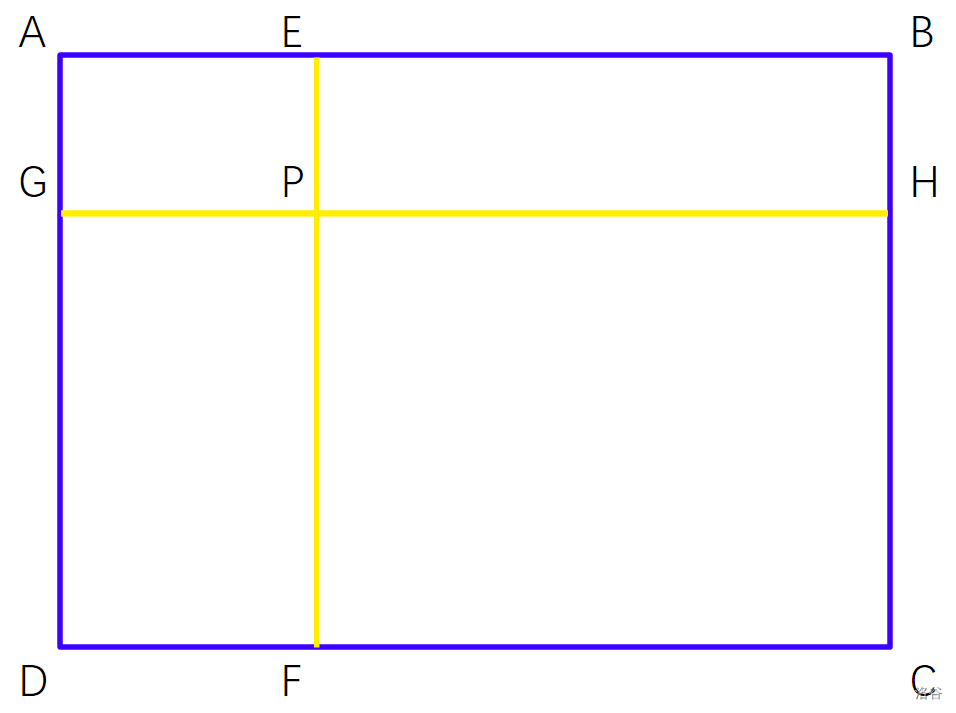
以 \(S(ABCD)\)代表矩形 \(ABCD\) 中的钉子数量。那么，在图中，如果需要求 \(S(PHCF)\) ，易知：

\(S(PHCF)=S(ABCD)-S(EBHP)-S(GPDF)-S(AEPG)\)

那么我们在上式中间两项分别加上 \(S(AEPG)\)，得：

\(S(PHCF)=S(ABCD)-S(ABHG)-S(AEDF)+S(AEPG)\)

译为中文，就是：左上角为 \(a[i_1][j_1]\) 右下角为 \(a[i_2][j_2]\) 的矩形中,有\(a[i_2][j_2]-a[i_1-1][j_2]-a[[i_2][j_1-1]+a[i_1-1][j_1-1]\) 个钉子。

然后就这么做了，于是 38分 。

发现超时的那个测试点全部是没钉子，回到样例 #1 后，发现只要钉子数不超过 1 ，那么挂的画在任何位置都可以。

显然，每行 \(m\) 个中有 \(m+(m-1)+...+2+1=\frac{m(m+1)}{2}\) 排列组合方式，每一列同理。

故一共有 \(\frac{m \times (m+1) \times n \times (n+1)}{4}\) 种排列组合方式

遂 AC 。

代码如下

#include <bits/stdc++.h>
#define ll long long
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
ll n,m,ans;
string s;
ll a[514][514];//存的是左上的钉子数
//思路是前缀和，但是这题用的二维
int main(){
	ios;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>s;
		for(int j=1;j<=m;j++){
			a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
			if(s[j-1]=='#')a[i][j]++;
		}
	}
	if(a[n][m]<=1){
		cout<<n*m*(n+1)*(m+1)/4;
		return 0;
	}
	int f;
	for(int i1=1;i1<=n;i1++){
		for(int j1=1;j1<=m;j1++){
			for(int i2=i1;i2<=n;i2++){
				for(int j2=j1;j2<=m;j2++){
					f=a[i2][j2]-a[i1-1][j2]-a[i2][j1-1]+a[i1-1][j1-1];
					if(f<=1)ans++;
					if(f>1)break;
				}
			}
		}
	}
	cout<<ans;
	return 0;
}

感谢阅读。