题解：P11797 【MX-X9-T1】『GROI-R3』Another Me

我们知道:

\(|x|=|x-0|\)

即一个数的绝对值是它在数轴上表示的点与原点的距离

---

稍作思考，画一个图(以样例一为例):

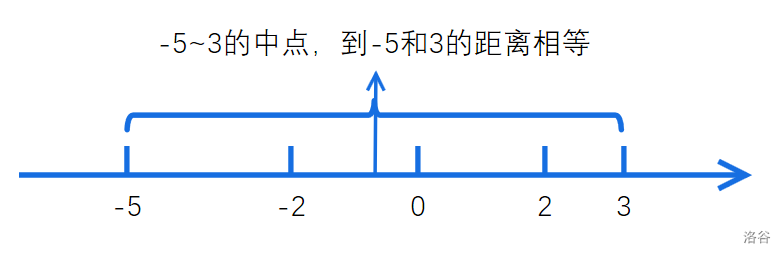
显然，所有数据绝对值的最小值就是最大值与最小值分别到原点距离的最小值。容易想到令这两点的中点为原点重新建立数轴，从而求出最小绝对值。

---

以现在建立的数轴:

\(|x'|=|x'-0|\)

显然最短距离是左右端点距离的一半。

简而言之，求出最大值与最小值之差的一半(显然是向上取整)再输出即可。

---

AC代码:

#include <bits/stdc++.h>
using namespace std;
int n,a,ans;
int amin=2147483647,amax=-2147483648;//方便后文取最小值与最大值操作
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a;
		amin=min(amin,a);
		amax=max(amax,a);
	}
	ans=amax-amin;//显然,amax>=amin,因此amax-amin>=0,故不需要绝对值
	cout<<(ans+1)/2;//向上取整
	return 0;
}

蒟蒻第一篇题解（求大佬指点）