POJ 3481 Double Queue 双队列

这个题应该是最近刷过的题里最费劲的了，但是也学到了很多新的数据结构和思想。

本题的无外乎三种操作：向数据结构中添加一个元素、取去权重最大的元素、取出权重最小的元素。

当然可以用数组来实现，在添加的时候使用二分查找来插入一个元素，但是这样做很耗时间。

既然每次只需要权重最大、最小的元素，这点与堆很像，而且堆插入一个元素也非常容易。

但是堆只能取最大堆、最小堆，总不能同时建立两个堆吧？

在网上搜索了相关资料，了解到一种叫做treap的数据结构，它是heap(堆)和tree（树）的结合版，这里的树是二叉搜索树。

treap的本质是数据用二叉平衡树获取，采用随机数来维护堆。

在了解treap之前，首先来了解一下二叉搜索树和堆吧：（对这两个数据结构熟悉的可以跳过这一段）

堆：我们常用到的优先队列，实际上就是以堆为基础的。堆分为两种，最大堆和最小堆，这里以最小堆为例来介绍堆的性质。堆实际上也是二叉树的一种。

最小堆：在最小堆中，每一个子节点的值都不大于它的父节点的值。 关于堆，首先它有两个最基本的操作，其他衍生操作都是在这两个基本操作的基础上进行的。这两个操作分别是把堆中的一个元素向顶层移动到一个合适的位置，以及把堆中的一个元素向底层移动到一个合适的位置。在这两个的基础上，还有两个基本思想：路径压缩和按秩合并，这些都是用来维持堆的平衡的。从这些操作衍生出插入一个元素、删除一个元素、堆排序、把一个数组转化为堆等算法。详细的实现过程这里不多介绍了，请搜索“堆的实现”。

关于二叉搜索树：对于二叉搜索树中的任意一个节点，如果他有左子树，那么该节点的值比它左子树上任意一个节点的值都要大，如果它有右子树，那么该节点的值比它右子树上任意一个节点上的值都要小。具体的实现可以搜索“二叉搜索树的性质和实现”。

treap与二叉搜索树十分类似，都是通过找到最左、最右节点来获取最值，不同的是它采用了堆的方法来维护这棵树。
treap对每个节点都会用生成随机数的方法赋予一个随机数值，利用随机数值来维护这棵二叉树的平衡。

总结一下，就是使用随机数来维护这棵树，但是寻找最值的方式和BST一致。所以关键点就是增、删和维护的操作。首先介绍维护这棵树的操作：旋转，然后再介绍增删节点的操作。 旋转：旋转分为左旋和右旋，分别表示两种维护操作。

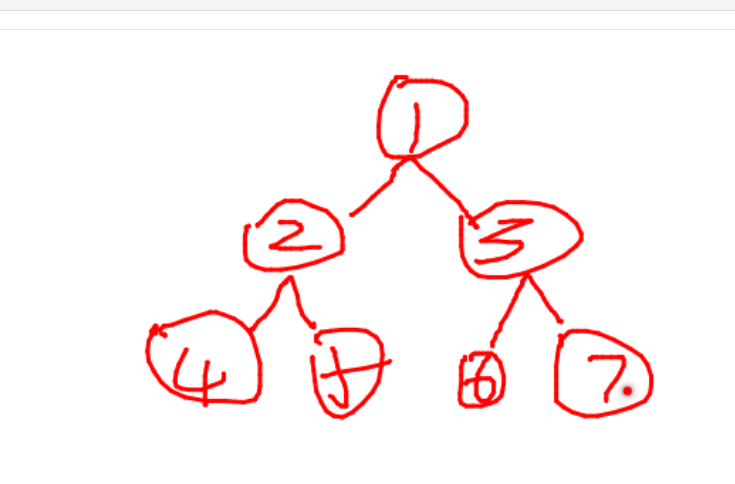
这是一棵二叉树，左旋后，把根节点右孩子作为新的根节点，原来的根节点作为新的根节点的左孩子，新根节点的左孩子作为旧根节点的右孩子，看上去就相当于向左旋转了，然后把新根节点3号多出来的孩子送给失去一个孩子的旧根节点1号。如下图：

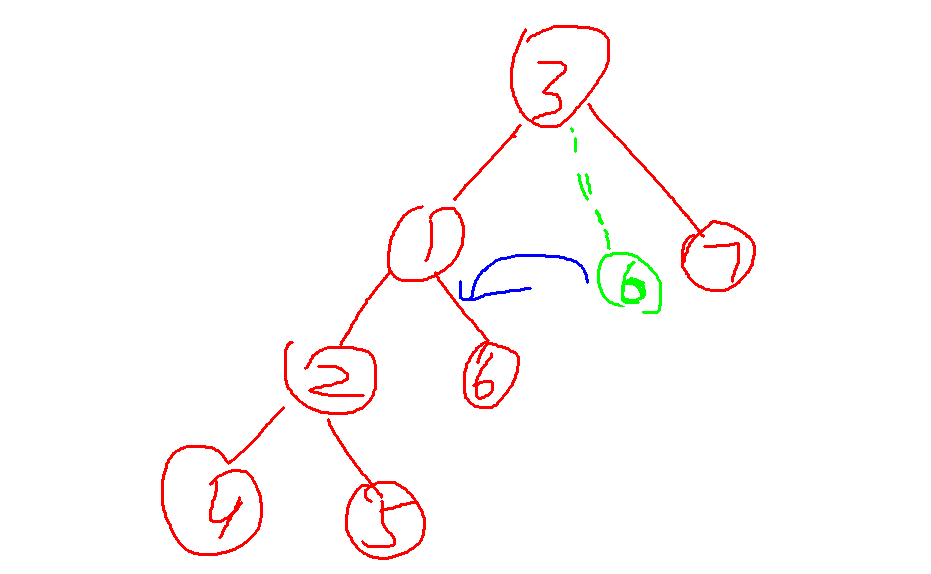
右旋同理，这里就不画图了，可以另找资料。
插入：就跟BST的插入操作一样，只不过插入后都要比较它和它的孩子的优先级，以此决定是否需要旋转（因为插入是首先跟根节点比较，再逐渐向下层比较的，所以不需要比较它和它的父节点的优先级。）
删除：删除的情况比较复杂，首先是如果删除的节点上存在多个元素，只需要让它的个数减一即可，如果存在一个，而且没有子节点，那么直接删除即可；若删除的节点没有右子节点，或左子节点的优先级高于右子节点，就将以删除元素为根的子树右旋。（使得左孩子变为以删除元素为根的子树的根元素），此时只需要删除新的右子节点。否则，就将以删除的元素为根的子树左旋，继续删除新的左子节点。

具体的实现代码这里不多写，请直接看最下面的代码即可。

#include<iostream>
#include<algorithm>
#include<stdlib.h>
using namespace std;
/*
* 本题应当采用treap的数据结构
* treap的本质是数据用二叉平衡树获取，采用随机数来维护堆
* 但是因为直接采用二叉链表的方法会导致超时，所以将数据结构改为使用索引数组
*/
#define MAX 500010
struct Node {
	int K;
	int P;
	int random;
	int left, right;	//利用值是否为0来判断是否是叶子节点
	int size;
	int countK;
} nodes[MAX];
int index = 0;
int root;

int getNewNode(int k, int p) {
	nodes[++index].K = k;
	nodes[index].P = p;
	nodes[index].random = rand();
	nodes[index].countK = nodes[index].size = 1;
	return index;
}
void addSize(int no) {
	nodes[no].size = nodes[nodes[no].left].size + nodes[nodes[no].right].size + nodes[no].countK;
}
void init() {
	getNewNode(0 ,-0x3f3f3f3f);	//1
	getNewNode(0, 0x3f3f3f3f);	//2
	root = 1;
	nodes[1].right = 2;
	addSize(1);					//1是父节点
}
void rotateRight(int &node) {
	int temp = nodes[node].left;
	nodes[node].left = nodes[temp].right;
	nodes[temp].right = node;
	node = temp;
	//必须从下向上计算size，否则会出错
	addSize(nodes[node].right);
	addSize(node);
}
void rotateLeft(int& node) {
	int temp = nodes[node].right;
	nodes[node].right = nodes[temp].left;
	nodes[temp].left = node;
	node = temp;
	addSize(nodes[node].left);
	addSize(node);
}
void insert(int& node, int k, int p) {
	if (!node) {
		node = getNewNode(k, p);
		return;
	}
	if (nodes[node].P == p)nodes[node].countK++;
	else if (p < nodes[node].P) {
		insert(nodes[node].left, k, p);
		if (nodes[nodes[node].left].random > nodes[node].random) rotateRight(node);
	}
	else
	{
		insert(nodes[node].right, k, p);
		if (nodes[nodes[node].right].random > nodes[node].random) rotateLeft(node);
	}
	addSize(node);	//重新计算node的size值
}
void remove(int& node, int p) {
	if (!node) return;
	if (nodes[node].P == p) {
		if (nodes[node].countK > 1) nodes[node].countK--;
		else if (nodes[node].left == 0 && nodes[node].right == 0) {
			node = 0;
		}
		else
		{
			if (nodes[node].left == 0 || nodes[nodes[node].right].random > nodes[nodes[node].left].random) {
				rotateLeft(node);
				remove(nodes[node].left, p);	//原先的结点到了左分支上
			}
			else
			{
				rotateRight(node);
				remove(nodes[node].right, p);	//右旋后原先的节点到了右分支上
			}
		}
	}
	else if (nodes[node].P > p) remove(nodes[node].left, p);
	else remove(nodes[node].right, p);
	addSize(node);
}
int getPbyPos(int node, int pos) {
	if (!node) return 0x3f3f3f3f;
	if (nodes[nodes[node].left].size >= pos) return getPbyPos(nodes[node].left, pos);
	else if (nodes[nodes[node].left].size + nodes[node].countK >= pos) {
		cout << nodes[node].K << endl;
		return nodes[node].P;
	}
	else return getPbyPos(nodes[node].right, pos - nodes[nodes[node].left].size - nodes[node].countK);
}

int main() {
	index = 0;
	init();
	int op;
	int totalNum = 2;
	int k, p;
	while (cin >> op,op) {
	if (op == 1) {
			cin >> k >> p;
			insert(root, k, p);
			totalNum++;
		}
		else if (op == 2) {
			if (totalNum == 2)cout << 0 << endl;
			else
			{
				p = getPbyPos(root, totalNum-1);
				remove(root, p);
				totalNum--;
			}
		}
		else
		{
			if (totalNum == 2)cout << 0 << endl;
			else
			{
				p = getPbyPos(root, 2);
				remove(root, p);
				totalNum--;
			}
		}
	}
	return 0;
}