2025.6.12 模拟赛

6.12 模拟赛

rect - CF1666A

所有点都在环里 \(\Leftrightarrow\) 所有点入度为 \(1\)。

key：每个左端点对应的宽度只有一种。

注意到形如 RL 的自由度是非常高的，那么考虑 RL 连续段后的第一个字符：

• 若是 U 或 L，一定指向外面或前面的某个 RL，直接寄掉
• 若是 R，由于它右边的不是 L，则只能由下面的 U 提供入度，且必须是字符串上它后面的第一个 U。
• 若是 D，考虑它右边的 L 连续段，最后一个 L 需要一个 U 提供入度，且必须是后面的第一个 U（若没有 L 则就是这个 D 本身）。

这样就能确定每个左端点对应的唯一宽度。

判断某段区间是否合法，要求入度矩阵恰是全 \(1\) 矩阵。考虑哈希，对于每一行，用上一行的 D，下一行的 U，这一行的 LR 左/右移拼起来，判断是否等于全 \(1\) 的哈希值即可。

注意到某行可以成为一个矩形的结束，当且仅当这一行不需要下一行的 U 即可合法。

将宽度相同，下标值模宽度相同的左端点放在一起处理。从后往前考虑每一行，注意特判 RL 串的贡献。

复杂度 \(O(n\sqrt n)\)：

• \(len\le \sqrt n\)：\(len\) 种余数，\(\frac{n}{len}\) 行，复杂度 \(O(n)\)。
• \(len>\sqrt n\)：只有 \(<\sqrt n\) 行，一共 \(O(n)\) 个数。

reset

先把 \(w\) 从小到大排序。

考虑可以凑出的 \((a,b)\) 形如什么样子。

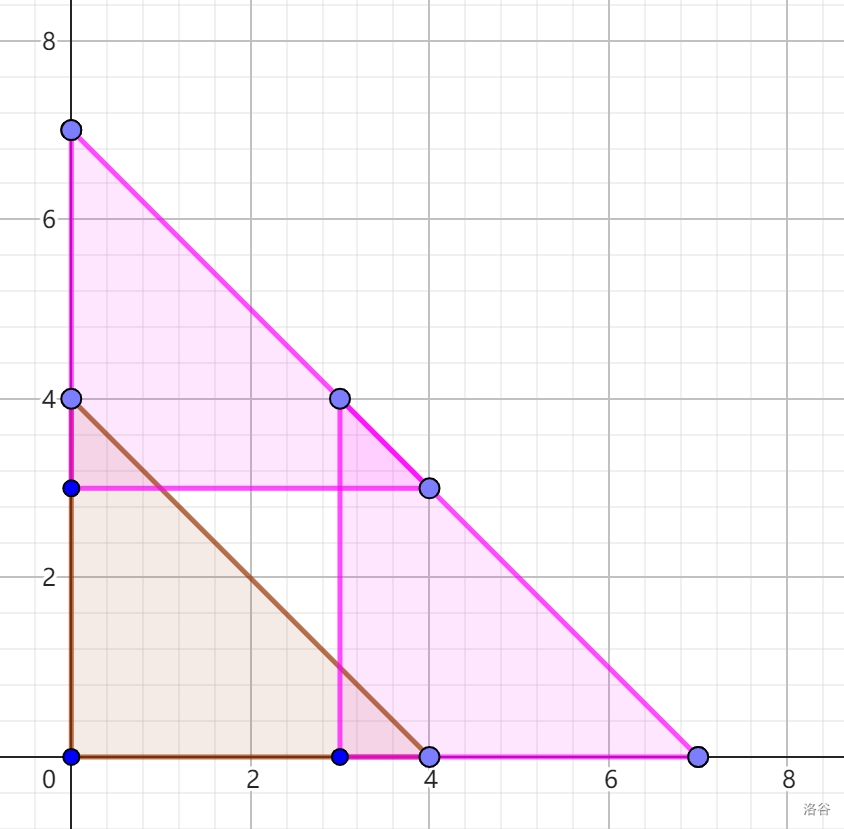
设当前可以凑出的集合为棕色三角形。如左图，加入一个 \(w_i=3\)，新的可以凑出的集合为两个粉色三角形（包含边界）。此时，仍然可以凑出 \(a+b\le s'\) 的所有 \((a,b)\)。

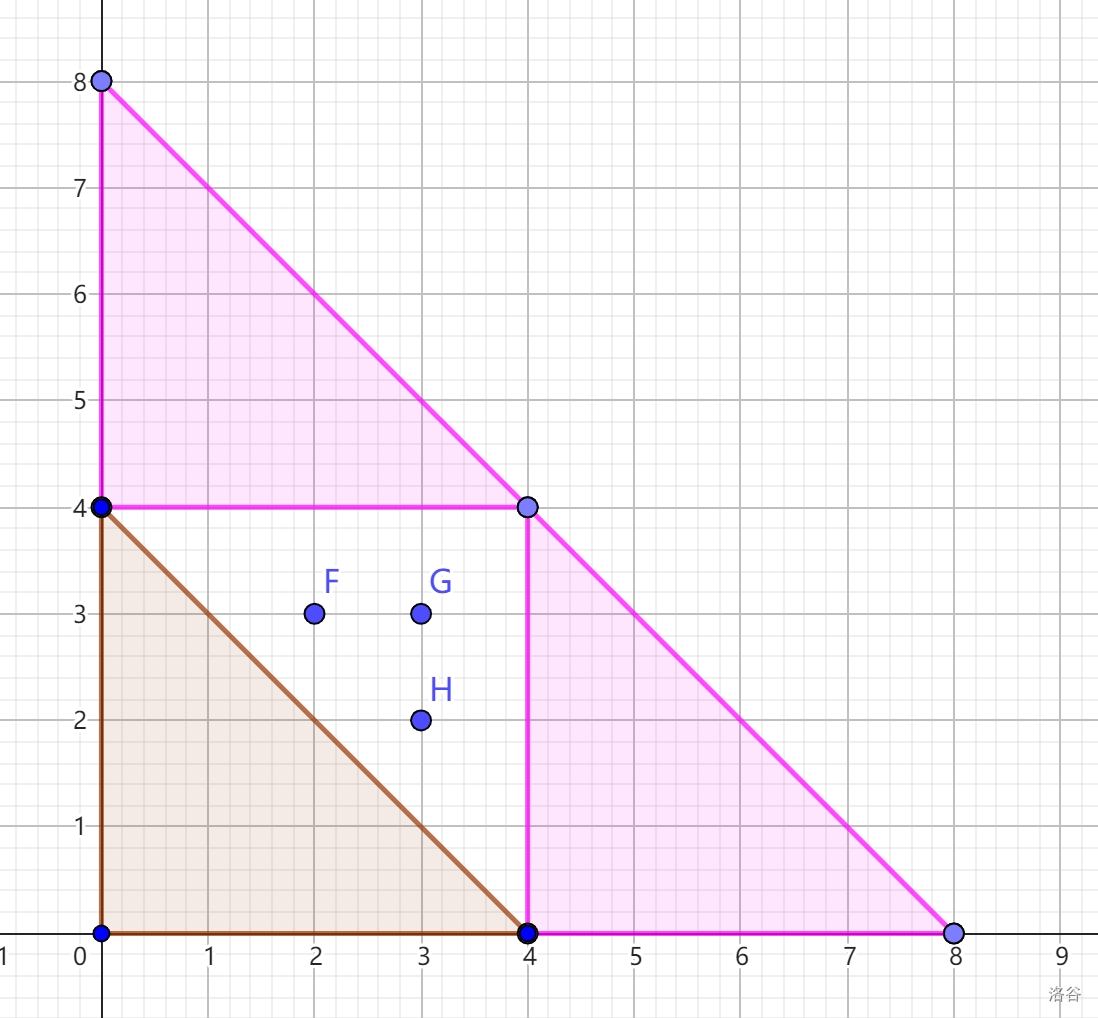
若加入一个 \(w_i=4\)，则形如右图。其中 \(F,G,H\) 三个点是凑不出的。而询问的是一个矩形，故对于 \(s<a+b\le s'\) 的询问 \((a,b)\)，要求 \(\min(a,b)<x_H\) 才能合法。

容易推出，当且仅当 \(2w_i>s_{i-1}+2\) 时会产生不合法点。对每个 \(i\) 维护前缀不合法点纵坐标最小值 \(g_i\)。

对每个询问二分出 \(s_{i-1}<a+b\le s_i\) 的位置，当且仅当 \(k\ge w_i\) 且 \(\min(a,b)<g_i\) 时回答 Yes。

young

杨表神秘题，不懂