2025.5.2 模拟赛
5.2 模拟赛
来自 BDF 的 神秘 AT 场
stardust
签到题,bitset 优化背包即可
nullstar
看起来很神秘,实则是找规律 + dp
容易发现,条件等价于:
若左上右下都是
1, 则右上左下也是1
从下到上考虑 1 的分布,形如若干个从左下到右上排布的上阶梯。
0 0 0 0 0 0 1
0 0 0 1 0 1 1
0 0 1 1 0 1 0
1 0 1 0 0 0 0
于是设 \(f(i,j,k)\) 表示第 \(i\) 行,最右边的 1 是在第 \(j\) 列,一共有 \(k\) 个 1 的方案数。
转移时,先考虑下面第一行有 1 的,枚举这个阶梯内的 1 的数量;然后再考虑在右边增加 1,形成新的阶梯。
有一些边界 01 的细节,需要前缀和优化。
三维空间开不下,需要滚动数组优化。
namespace zj{
int f[N][N];
int sm1[N][N],sm2[N],sm3[N][N];
inline void solve(){
getC();
// 初值
f[0][0]=sm1[0][0]=1;
rep(j,1,m) {
rep(k,1,j) f[j][k]=C[j-1][k-1],sm1[j][k]=f[j][k];
per(k,j,0) sm1[j][k]=pls(sm1[j][k],sm1[j][k+1]);
}
per(i,n-1,1){
// 从下面的阶梯转移
memset(f,0,sizeof(f));
rep(j,1,m) rep(k,0,j) {
f[j][k]=pls(f[j][k],sm1[j][max(k,1)]);
}
// 向右拓展
memset(sm2,0,sizeof(sm2));
rep(j,1,m) {
rep(k,1,j) {
f[j][k]=pls(f[j][k],sm2[k-1]);
}
rep(k,0,j) sm2[k]=pls(sm2[k],f[j][k]);
}
// 下面都是 0,从第 i 行开始
f[0][0]=1;
rep(j,1,m) rep(k,1,j) f[j][k]=pls(f[j][k],C[j-1][k-1]);
memset(sm3,0,sizeof(sm3));
rep(j,1,m) {
rep(k,0,j) sm3[j][k]=pls(sm3[j][k],f[j][k]);
per(k,j,0) sm3[j][k]=pls(sm3[j][k],sm3[j][k+1]);
}
rep(j,1,m) rep(k,0,j) sm1[j][k]=pls(sm1[j][k],sm3[j][k]);
}
int ans=1;
rep(j,1,m) rep(k,0,j) ans=pls(ans,f[j][k]);
printf("%d\n",ans);
}
}
ophelia
神秘性质题,笔者希望尽力解释寻找这些性质背后的想法。
记号约定:$\to $ 表示边定向,$\Rightarrow $ 表示能直接/间接到达。
参考:jun头吉吉
真难则反,“满足任意一种” 转化成 “两种都不满足”。
于是转化为同时满足:
- 入度 \(\le k\)。
- 不存在形如三元环指向同一个点的导出子图。
显然度数限制是弱的,子图限制是强的。
Lemma 1:竞赛图存在任意环则定存在三元环。
证明采用归纳,考虑从一个点开始不断缩环,最后一定只剩下三元环。
则我们可以想办法把竞赛图限定成 DAG,而竞赛图如果是 DAG,就会有确定的形态:
- 有向无环竞赛图的拓扑序对应图上的一条有向链。
- 不妨记为 \(x_1,x_2,\dots,x_k\),则 \(\forall i<j,x_i\to x_j\)。
这对于我们的后续分析是非常有利的,于是考虑找到 DAG 的限制。
竞赛图计数的经典套路是删 \(0\) 度点,去掉 \(i\) 个 \(0\) 度点的方案数是 \({n\choose i}i!\)。
接下来,考虑找到“指向”的这个点,不妨任意钦定一个点 \(v\),记它的入度点集为 \(X\),出度点集为 \(Y\)。
Lemma 2:\(X\) 导出子图为 DAG。
这是显然的,接下来考虑证明 \(Y\) 导出子图也没有三元环,即若存在三元环,定不合法。
记三元环为 \((a,b,c)\)。
找到非环内的点 \(w\in Y\),若 \(a\to w,b\to w,c\to w\),则不合法(如图3)。
否则,\(\forall w\in Y\),\(w\Rightarrow a,b,c\)。
Lemma 3:若 \(w,w'\in Y,u\in X,w\to u,w\Rightarrow w'\),则 \(w'\to u\)。
证明如图1,\(4\) 个点确定 \(5\) 条边,已经有了三元环 \((u,v,w)\),那么 \(w'\to u\) 就被确定了。
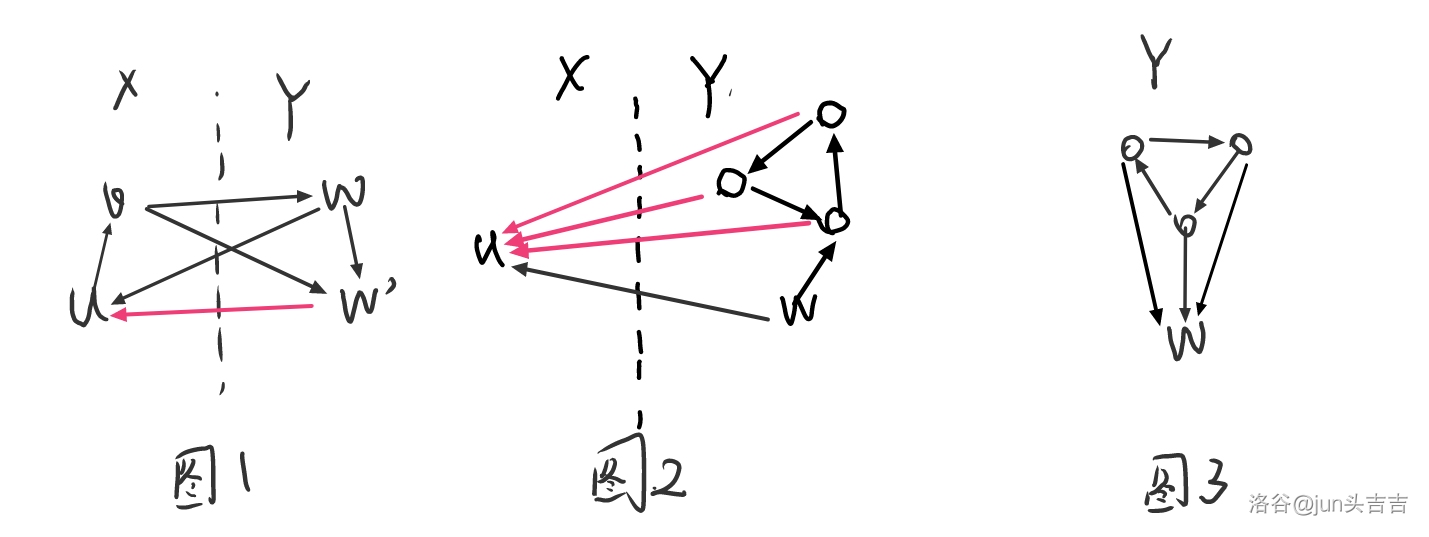
(借用一下这位老师的图)
由于 \(w\Rightarrow a,b,c\),\((a,b,c,u)\) 就形成了非法子图(如图2)。
而由于每个点至少有一个入度,取 \(u=x_1\) 则一定可以找到合法的 \(w\)。
Lemma 4:Y 的导出子图是 DAG。
接下来,\(X,Y\) 两部分内部已经变成链了,考虑 \(X,Y\) 之间的边(这一部分是最神秘的)。
注意到,在 Lemma 4 的前提下,Lemma 3 可以改写为:
- 若 \(y_j\to x_i\),则 \(y_{[j,l]}\to x_i\)
显然,一定有 \(y_l\to x_1\)。
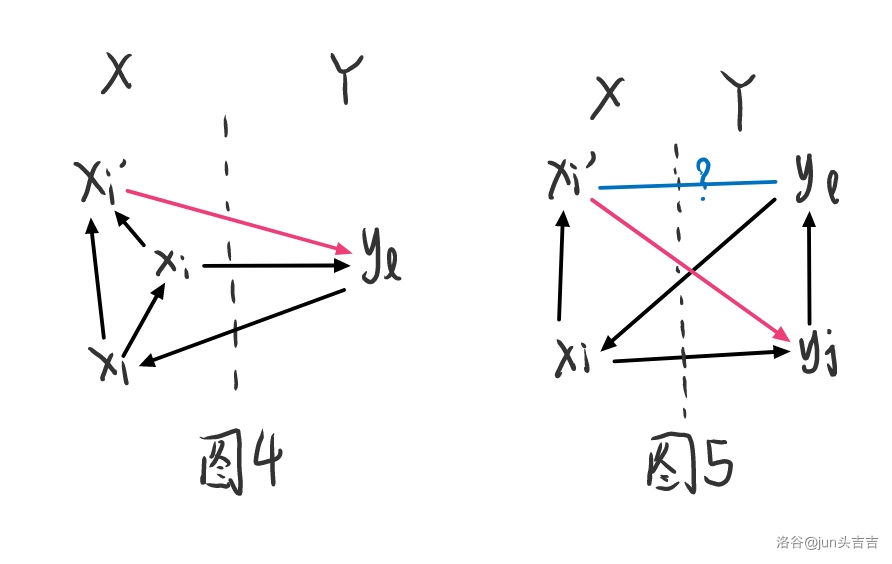
我们还是考虑寻找三元环,如图 4,此时 \((x_1,x_i,y_l)\) 形成了三元环。
Lemma 5:若 \(y_l\not\to x_i\),则 \(y_l\not\to x_{[i+1,k]}\)。
此时 \(y_l\) 向 \(X\) 集合连边形如:
- 对于 \(i\in [1,t]\),\(y_l\to x_i\)。
- 对于 \(i\in [t+1,k]\),\(y_l\not\to x_i\)。
Lemma 6:若 \(y_j\to x_i\),则 \(y_j\to x_{[1,i]}\)。
如图5,若存在 \(i\in [1,t],y_j\not\to x_i\),则 \(x_i,y_j,y_l\) 形成了三元环,若 \(y_j\to x_{i'}\) 则 \(y_l\to x_{i'}\),形成了不合法子图。
可以验证,满足了上述条件的图,就一定符合题目要求。
接下来考虑刻画 \(X\),\(Y\) 之间的连边,发现在 \(k\times l\) 的网格图中形如右下阶梯。
00111111
00000111
00000011
00000000
(\(0\) 表示 \(x_i\to y_j\))
注意到,\(y_l\to x_1\),则 \((1,l)\) 一定是 1;\(x_k=v\) 则最后一行一定全 0。
容易从左到右 dp 出合法网格图的数量。
对于度数限制,考虑 \(X\) \(Y\) 集合分别的贡献,在 dp 过程中判断即可。
code:
int f[N][N];
inline int calc(int k,int l,int lm){
f[0][0]=1;
rep(j,1,l){
int sum=0;
rep(i,0,k){
sum=pls(sum,f[j-1][i]);
if(i-1+l-j+1<=lm && j-1+k-i<=lm)
f[j][i]=sum;
else f[j][i]=0;
}
}
int res=0;
rep(i,1,k-1) res=pls(res,f[l][i]);
return res;
}
int fac[N],ivf[N];
inline int calc(int n,int k){
if(n==1) return 1;
int res=0;
rep(i,1,k+1) res=pls(res,calc(i,n-i,k));
return mul(res,fac[n-1]);
}
int main(){
int n,k;read(n),read(k),read(mod);
fac[0]=ivf[0]=1;
rep(i,1,n) fac[i]=mul(fac[i-1],i);
ivf[n]=fp(fac[n],mod-2);
per(i,n-1,1) ivf[i]=mul(ivf[i+1],i+1);
int ans=0;
rep(i,0,k) ans=pls(ans,mul(calc(n-i,k-i),mul(fac[n],ivf[n-i])));
printf("%d\n",mul(mns(fp(2,n*(n-1)/2),ans),fp(fp(2,n*(n-1)/2),mod-2)));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号