2024 暑假训练记录

2024 暑假集训记录

Day 1 - 7.7

教练发了 2015 BJ JL HN 省队集训，大概把 BJ 的题顺了一遍，感受是十年前的题目都好板啊...

ppt 还没来得及看，只简单看了几个

2015 BJ 省队集训

Day 2 - 7.8

继续看 BJ 省队集训题，写题解。发现即使很板，但是数据范围好鬼啊...

我是不是该写几个板子复健了（？

Day 3 - 7.9

上午学习 Splay，下午写树套树，已经没有码力了/kk

经过一下午的努力我的树套树从 70 变成了 80（笑

Day 4 - 7.10

题目质量的确不高，不过 std 写的不错。

queue

求长为 n，不包含 111 和 101 的 01 串数量，答案对 10007 取模。

数据范围 $n\le 10^{18}$

key: 矩阵优化 dp

记录后两位的值，写出转移矩阵，直接矩阵快速幂就做完了。

神奇的 std：$A^{2p-2}\equiv I\pmod p $，故只需递推前 20012 个即可。

paths

n 个点的树，树上有 m 条路径，问最多能选几条不相交路径。

数据范围：$n,m\le 2\times 10^5$

赛场做法：树剖 + 树上 dp

设 $f(u,0/1)$ 表示点 u 的子树内，选/不选 u 的最多路径数。

$f(u,0)=\sum \max f(v,0/1)$

枚举以 u 为 lca 的路径 (a,b)，记路径上的点为 $a_1=u,a_2,\cdots,a_k=a$

$f(u,1)\leftarrow \sum f(a_i,0)-\max f(a_{i+1},0/1)$

把求和号拆开，得到两个和都可以用树剖维护。
注意后面那个不包括 u。

std：贪心

若路径相交，选 lca 深度较大的一定不劣。

感性理解，正确性大概比较显然。

palacinke

n 点 m 边的有向图，每条边上有四种货物中的某几种。经过一条边需要 1 分钟，买货物需要 1 分钟（不管买了多少）。从点 1 出发，最终回到点 1，四种货物必须都买。求在 T 分钟内，有多少种方案。

数据范围 $n\le 25,m\le 500,T\le 10^9$

sub1&2 $T\le 500$ ：暴力状压 dp

$f(t,u,op)$ 表示时间 t，位置 u，买东西状态 op。

$\begin{aligned} f(t,u,op)&\to f(t+1,v,op)\\ &\to f(t+2,v,op|w) \end{aligned}$

复杂度 $O(mT2^k)$

sub3 $n\le 5$ ：矩阵优化 dp

压成一个 $r=5\times 16\times2$ 的矩阵，复杂度 $O(r^3\log T)$

sub4 所有边都是四种都有：随便走 - 完全不买

key：拆点，把“买东西”拆出一条边

只需一个 $50\times 50$ 的邻接矩阵。

正解：容斥

随便走 $-$ 一个不走 $+$ 两个不走 $-$ 三个不走 $+$ 四个不走

枚举 16 种情况，建邻接矩阵时有些买东西的边不连就行。

key：建立汇点，强制最后一次回到 1 是回到汇点

在汇点建立自环，让“不超过T”都变成 T，最后答案就是汇点的矩阵值。

ogledala

有 m 个石子，初始已经挖掉 n 个 $a_1,a_2,\dots,a_n$。

重复下列操作：

找到当前最长的一段连续的石子，若有多段，取最左边的
挖掉最中间的石子，若段长为偶数，则挖掉靠左那个

Q 次询问第 $b_i$ 次操作挖掉的是哪颗石子。

数据范围：$n,Q\le 10^5,m\le 10^{14}$

sub1&4 $b_i\le3\times 10^5$：堆模拟

正解：二分

初始连续段最多只能分出 $\log$ 种不同长度的段

由于任何时刻，一定是从长度最长的段开始分，于是我们可以顺序计算出每种长度的段都有多少个。

排序询问，利用双指针思想，定位分的是长度为 len 的段，并知道是初始第 id 段里的第 num 个 len。

知道在哪一段后，就可以二分出位置。因为可以计算出任意长度的连续段分出的长度为 len 的段的数量。

code：

LL f(LL nw,LL want){// 原长为 nw，能分出长为 want 的段的数量
    if(nw<want) return 0;
    if(nw==want) return 1;
    if(dp.find(nw)!=dp.end()) return dp[nw];
    return dp[nw]=f(nw>>1,want)+f((nw-1)>>1,want);
}
LL query(LL l,LL r,LL len,LL num){
    LL mid=(l+r)>>1;
    if(r-l+1==len) return mid;
    if(f(mid-l,len)>=num) return query(l,mid-1,len,num);
    return query(mid+1,r,len,num-f(mid-l,len));
}

Day 5 -7.11

interview

给定序列 $a_n$，求最小的 $x$ 使得前缀 $a_1 \dots a_x$ 中，可以选出 $m$ 个数，极差不超过 $k$。

数据范围：$n,m,k\le 10^5$

key：转化为值域上问题

二分 + 值域上滑动窗口
记录 $num_i$ 表示值域 $[i,i+k-1]$ 有多少个数，线段树维护

task

两台机器 A B，有 $n$ 个任务要安排，要求第 $i$ 个任务开始时，前 $i-1$ 个任务均已完成或正在运行。每个任务在 A B 上运行的时间不同，问最少需要多长时间完成所有任务。

数据范围：$n\le 2000,tA,tB\le 3000$

sub 1&2 $n\le 200,tA,tB\le 300$：$O(n^2w)$ dp

$f[i][j][0/1]$ 表示第 i 个任务在 A/B 上运行，开始时间为 j，另一台机器最早结束时间。

转移平凡，注意第 i 个任务要等第 i-1 个任务开始才能开始。

正解：$O(nw)$ dp

key：最优解时间差不超过 $2mx$ 且某个任务可以开始的时间区间很小

$f[i][j][0/1]$ 表示第 i 个任务在 A/B 上运行，自己的结束时间，且与另一台机器的结束时间差为 j

转移同样平凡，注意数组别开小了。

diamond

有一个序列 $p_i$ 服从 $[1,m]\cap \N$ 的等概率分布，从 1 到 n 执行如下操作：

若 $p_i\in S_i$，选择 $p_i$，结束操作
否则，$i\to i+1$，且之后不能再选择 $p_i$

对于每个 $i$，构造 $S_i$ 使得最终选择的值期望最大，求这个期望。

数据范围 $m\le 10^5,n\le 10^9$

key：期望 dp + 分段矩阵乘

记 $E_i$ 表示序列长度为 i 时的期望值（倒推）
$E_i=\frac{1}{m}\sum\limits_{v\in S_i}v + \frac{m-|S_i|}{m}E_{i-1}$

若干结论：

$S_1$ 一定是全集
$S_i$ 一定选一段后缀
$|S_i|$ 单调不升
key：$S_i=[\lceil E_{i-1}\rceil,m]$（不选还有 $E_{i-1}$，更小的干脆不选）

显然可以线性递推 $E_i$。

发现 $E_{i-1}$ 的系数只与 $\lfloor E_{i-1} \rfloor$ 有关，而 $\lfloor E_{i-1} \rfloor$ 只有 $m$ 种取值，于是可以分段矩阵乘。

二分出每段的右端点，check 方法就是直接判断 $\lfloor E_{cur}\rfloor=k$

复杂度 $O(m\log n)$

control

$n$ 个点的有根树，根节点为 1。
对于 $k=1,2,3,\cdots,n$，在树上选择 $k$ 个关键点。设 $t_i$ 表示 $i$ 到根的路径上距离 $i$ 最近的关键点到 $i$ 的距离。设 $a_k=\min_{所有选择关键点的方案}\{\max t_i\}$，求 $a_1\dots a_n$ 的异或和。

数据范围 $n\le 2\times 10^5$

key：转化为使 $\max t_i\le x$ 至少需要 $b_x$ 个关键点

贪心地从深度最深的不合法点开始，选择它的 $x$ 级祖先，标记子树内所有点为合法。

神奇的事情在于，对于某个 x，最多只可能做 $O\left(\frac{n}{x+1}\right)$ 次标记。于是复杂度是调和级数 + 线段树维护标记（注意不应重建线段树，而应撤回标记）。

写法上，可以使用标记永久化的思想（类似李超线段树），但需注意 pushup 时要判好左右儿子分别被标记的情况。

Day 6 - 7.12

构造之神 —— devans

记录常见的错误，调代码的时候可以对照着排查——zzj

中午拉着全机房的人测 mbti 捏（
呈现了 mbti 多样化的局面...

CF1983B Corner Twist

唯一自己会做的题/kk

$n\times m$ 的 012 矩阵，每次操作：

选择一个至少 $2\times 2$ 的矩形
对其中两个对角格子 $+1$，另外两个 $+2$

问可否通过若干次操作，把矩阵 $A$ 变成 $B$。

key1：必要条件 $\to$ 加强成充分条件

整个矩阵的和 $\bmod 3$ 意义下不变（每次操作 +6）
每行 & 每列的和 $\bmod 3$ 意义下不变（每次操作 +3）

下证为什么是充要条件。

key2：简化操作 $\to$ 局部依次满足

显然，每次操作都可以拆成若干次选 $2\times 2$ 矩阵。
只考虑满足左上角，从左到右，从上到下依次操作。由于行列和不变，所以满足前 $n-1$ 行、前 $m-1$ 列后，第 $n$ 行、第 $m$ 列一定已经满足。

CF1730B Meeting on the Line

数轴上有 $n$ 个点 $x_n$，钦定一个点 $x_0$，最小化 $\max\{t_i+|x_i-x_0|\}$。

这题有弱智的 $O(n\log n)$ 三分做法，但思维点在线性做法。

key1：弱化问题 $\to$ 发现性质

如果 $t_i=0$，显然是选最左和最右点的中点。

key2：转化问题 $\to$ 保留性质

拆点成 $x_i-t_i$ 和 $x_i+t_i$，于是满足上述性质。

CF1391E Pairs of Pairs

给定 $n$ 点 $m$ 边的无向连通图，选一个问题完成：

找到一条点数 $\ge \lceil \frac{n}{2} \rceil$ 的路径
找到一个大小 $\ge \lceil \frac{n}{2} \rceil$ 的集合，对所有点两两配对，满足任意两对点的导出子图有 $\le 2$ 条边。

key：dfs 生成树没有横叉边

若存在深度 $\ge \lceil \frac{n}{2} \rceil$ 的点，直接选它到根的路径即可。

否则树的层数较小，直接每层的点两两配对，一定满足要求。

没有横叉边，所以导出子图最多有两条返祖边
每层最多扔掉一个点，而一共只有 $< \lceil \frac{n}{2} \rceil$ 层

三道类似的例题：

CF1508C Complete the MST

$n$ 个结点的完全图，给定 $m$ 条边的边权。给未赋权值的边赋值，使得所有边权异或和为 0，并最小化最小生成树的边权和。

数据范围 $n,m\le 2\times 10^5$

key1：一条边赋异或和，其他全 0

若有边不选进最小生成树，那么直接把这条边赋成异或和
否则怎么赋值都一样，这样做肯定不劣

key2：考虑给定边的稠密程度

$n\le O(\sqrt m)$ 即 $n\approx 750$，枚举哪条边赋值成异或和，直接跑最小生成树，复杂度 $O(m\sqrt m)$
$n> O(\sqrt m)$ 即给定边稀疏，一定有未赋值的边不选进最小生成树，直接当所有边权为 0，缩连通分量，跑给定边的最小生成树即可

如何求完全图删去 $m$ 条边的连通分量？
子问题 CF920E Connected Components?

key3：最大值 $\ge$ 平均值

删去 $m$ 条边相当于删去 $2m$ 个度数，也就是说剩下度数的平均值是 $n-1-\frac{2m}{n}$。

从度数最大的点开始考虑，不与它联通的点很少，最多只有 $\frac{2m}{n}$ 个，枚举每个点的联通情况，总复杂度 $O(m)$。

CF1508D Swap Pass

平面上 $n$ 个点，每个点上有值 $p_i$，若干次操作：

选择两个没有连边的点 $(i,j)$，连接 $(i,j)$
交换 $p_i,p_j$

要求线段不能有交（除端点外），给出操作方案使 $\forall i,p_i=i$。

保证不存在三点共线，$n\le 2000$

key1：局部问题 $\to$ 优秀性质

置换环：对于排列 $p_i$，连接 $(i,p_i)$，一定得到若干个环。

只有一个置换环的排列可以用菊花图完成
操作就是不断交换根 $x$ 和 $p_x$，显然这些边不会有交

key2：合并问题 $\to $ 保留性质

置换环内部交换 $\to$ 拆解置换环
置换环之间交换 $\to$ 合并置换环

考虑能否把所有点合并到一个置换环中。
首先连出一个菊花，显然的可以连接最外面的所有边，这样就全部合成一个置换环，且不会相交。

具体的，选择最左边的点为根，斜率排序，顺时针/逆时针合并置换环（并查集维护），若在一个置换环里就跳过，否则连边。
操作顺序是先合并置换环，再做菊花图。

习题： CF1491G Switch and Flip

CF1523D Love-Hate

$n$ 个人，$m$ 种货物，每人喜欢不超过 $p$ 种货物。求一个最大的子集，使得有 $\ge \lceil \frac{n}{2} \rceil$ 个人喜欢所有子集内的货物，输出方案。

数据范围 $n\le 2\times 10^5,m\le 60,p\le 15$

key：答案被超过 $\lceil \frac{n}{2} \rceil$ 个人喜欢 $\to$ 随机到喜欢答案的人概率极高

随机到某个人 x，认为答案是被他喜欢的，于是只有 $2^p$ 种可能。
扫一遍 $n$ 个人对这 $p$ 种货物的态度，一共也只有 $2^p$ 种，可以用桶存每种态度的人数。
每种态度只对它的子集有贡献，可以证明枚举子集的子集复杂度 $3^p$。
再扫一遍 $2^p$ 种答案，看哪些有 $\ge \lceil \frac{n}{2} \rceil$ 个人喜欢。
单次随机复杂度 $O(np+3^p+2^p)=O(3^p)$ 大约是 $2\times 10^7$，故可以随个差不多 50 次的。

证明枚举子集的复杂度
$\sum_i^p C_p^i \left(\sum_j^i C_i^j\right)=\sum_i^p C_p^i\times 2^i=3^p$（二项式定理）
还有一种高维前缀和的做法是 $O(p2^p)$ 的

CF1804F Approximate Diameter

$n$ 点 $m$ 边的初始无向图，$q$ 次添加一条边，询问图的直径。允许 $\frac{1}{2}ans\le out\le 2ans$ 的误差。

key1：$q=0 \to$ 类比树的直径

钦定一个点为起点，dfs 出最远点，这个距离一定在 $[ans/2,ans]$ 之间，记为“较优答案”。

key2：允许误差 $\to$ 二分可行区间

正确答案 & 较优答案单调不增

记正确答案为 $A_p$，“较优答案”为 $C_p$。
重复下述过程：

当前有答案 $C_{cur}$，二分可行区间右端点 $r$
check(p)：判断 $C_{cur}\le 2C_p$
$cur\to r+1$

为什么？$C_p\in [\frac{1}{2}A_p,A_p] \to 2C_p\in[A_p,2A_p]$，故 $C_{cur}\le 2C_p$ 一定安全，否则可能不安全（但我们不知道）。

显然 $C_{cur}$ 每次至少砍半，故只需二分 $\log$ 次。
总复杂度 $O(n\log^2n)$

Day 7 - 7.13

继续写昨天邹邹讲的题，还有 4 道没写/kk

Day 8 - 7.14

ak

n 堆石子 ${a_i}$，每次选连续的 $k$ 堆，最后剩下一堆。Y 先手 J 后手，Y 希望剩下的多，J 希望剩下的少。问最优策略下一共会拿走多少颗石子。

数据范围 $n\le 10^6,n\equiv 1\pmod k$

key: 只有 $i\equiv 1\pmod k$ 的才会剩下

每次一定拿走一个完系，且剩下的余数不会改变。
所以一共有 $\lceil\frac{n}{k}\rceil$ 个数，最后剩下的是中位数（若有偶数个，则是较大的那个）

loser

给定 $n$ 个节点的树，每个节点上有一个左括号或右括号，q 次操作：

反转 (x,y) 路径上所有括号
查询 $x\to y$ 的有向路径组成的括号序列中，最长的合法子序列的长度

数据范围 $n,q\le 10^5$

key：合法括号序列的数值表示

众所周知，令左括号为 $1$，右括号为 $-1$，合法括号序列的充要条件：

$\sum w_i=0$
$\min s_i\ge 0$（前缀和）

已知括号序列的权值和 $W$，前缀和最小值 $v$，为了方便，令 $s_0=0$，于是 $v\le 0$

若 $v<0$，删去最左边的 $-v$ 个右括号。
此时新的 $W\ge 0$，删去最右边的 $w$ 个左括号，剩下的就是合法括号序列。

线段树维护 $W,v$，树剖合并区间即可。
注意需要维护前缀 & 后缀的最大值 & 最小值，细节较多。

king

$n$ 个一类物品，$m$ 个二类物品。

对于每个一类物品，花费 1 单位代价收益 $a_i$
对于每个二类物品，花费 1 单位代价收益 $b_i$，或花费 2 单位代价收益 $c_i$

每种物品不能重复买，求花费不多于 $v$ 单位代价，最多能收益多少。

数据范围 $n,m\le 10^5,v\le 10^18,a_i,b_i,c_i\le 10^9$

首先 v 的数据范围是诈骗，实际最多只可能花费 $n+2m\le 3\times 10^5$ 的代价。

sub1 $v\le 10^3$：暴力 dp

sub2 $c_i=0$：贪心

正解：反悔贪心

key1：按照单价贪心

一类物品没啥好说的，二类物品有两种情况：

$b_i\times 2 \ge c_i$ ：拆成两个代价为 $1$ 的物品，$b_i$ 和 $c_i-b_i$
$b_i\times 2 <c_i$：显然不可能只选 $b_i$，直接捆成单价 $c_i/2$ 的物品

显然如果出现选不了的情况，只可能是最后剩下 1 单位代价，而下一个该选的是代价为 2 的物品。
此时有两种选择：

再选一个代价为 1 的物品
去掉一个代价为 1 的物品，选现在这个物品

注意，对于还没被选的二类物品，即使 $b_i\times 2<c_i$，$b_i$ 也是可以被选择的。

key2：直接反悔贪心

代价每增加 1，有 4 种情况：

选择一个代价为 1 的物品
升级一个代价为 1 的物品
失去一个代价为 1 的物品，选择一个代价为 2 的物品
降级一个代价为 2 的物品，选择一个代价为 2 的物品

这种设计满足最优子结构，直接堆维护反悔贪心即可。

Day 9 - 7.15

还没上班就想下班的 devout 小姐姐可爱捏

maxmex

给定序列 $\{a_n\}$，q 次询问 $\max\limits_{r-l+1=k} {\rm{mex}} _{i=l}^{r} a_i$

数据范围 $n,q\le 10^5$

看懂本题的 std 太费心力了/kk

记 maxmex 为 $f(k)$，显然 $f(k)$ 单调不降。枚举 $f(k)$ 的值，转化成求满足 $f(k) = v$ 的范围，即求最大的 $k$ 使得 $f(k)\le v$ 之类的。

从小到大枚举 $v$，显然一个区间的 ${\rm mex}= v$ 的必要条件是区间中没有 $v$，即 $v$ 的所有位置把序列分割成若干个部分，满足要求的区间一定是某个部分的子区间。

在平面直角坐标系上表示一个区间 $[l,r]$ 为点 $(l,r)$，一个部分 $[L,R]$ 为矩形 $(L,L)$ ~ $(R,R)$，满足要求的区间一定落在矩形并的内部。

我们希望知道 ${\rm mex }\le v$ 的区间，于是从小到大不断加入矩形，落在矩形并内就是充要条件。

我们要求对于 $r=l+k$ 的所有点，都落在矩形并内，即 $k= \min\limits_{l\in [1,n]} r_{max}-l$。

如图所示，所有矩形都“挂在” $y=x$ 这条直线上，矩形并形如一个阶梯。所以我们只需维护阶梯的左上顶点，可能更新 $\min\limits_{l\in [1,n]} r_{max}-l$ 的只有阶梯的拐点（绿色的线段）。

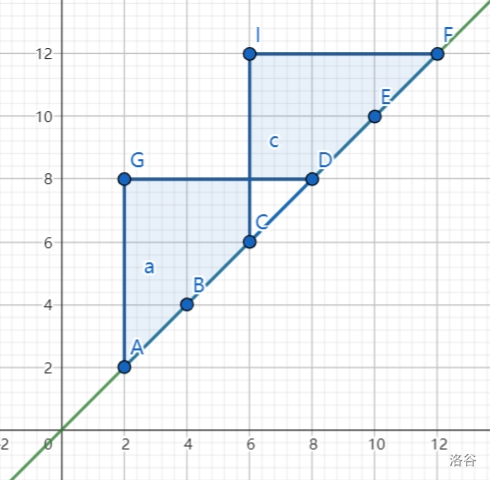
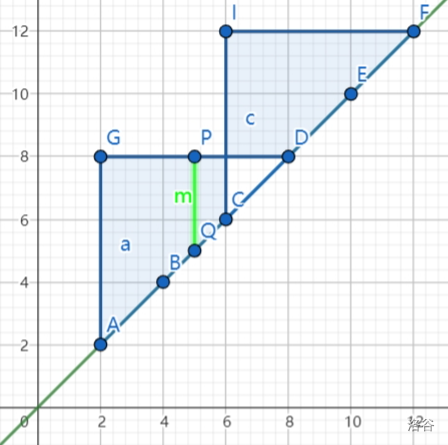
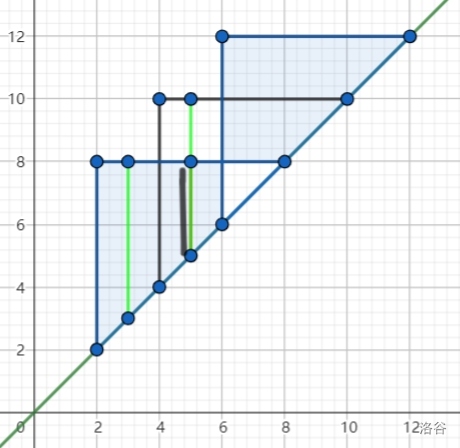
当我们加入一个新的区间，会有一些旧的绿色线段被覆盖，产生新的绿色线段（黑色的线段被覆盖，产生新的两个绿色线段）

具体维护过程看代码注释/kk

map<int, int> mp;
priority_queue<int, vector<int>, greater<int>> Q, DQ;

// mp 维护阶梯的所有顶点 (l,r)
// 可能成为答案的一定是阶梯的拐点
// Q 维护 r-l 最大值的最小值，DQ 维护应被删掉的 r-l 较小值
void ins(int l, int r) {
	//it 代表存横坐标 l 的顶点的指针
	auto it = mp.lower_bound(l);//找到横坐标 >=l 的第一个顶点
	if (it == mp.end() || it->first != l) {//如果 l 没有顶点
		if ((--it)->second >= r) return;//如果前面的顶点比 r 高，那么 (l,r) 一定在阶梯内
		Q.push(it->second - l);//l-1 成为新的拐点，塞进答案堆里
		it = mp.insert(make_pair(l, it->second)).first;//新建一个顶点，不赋值成 r 只是为了方便
	}
	if (r <= it->second) return;
	auto jt = next(it);//把 l 右边的拐点，被 [l,r] 覆盖的删掉
	if (jt == mp.end()) {it->second = r; return;}
	DQ.push(it->second - jt->first);
	while (jt != mp.end() && jt->second <= r) {// 所有高度低于 r 的拐点都会被删掉
		auto kt = next(jt);
		if (kt != mp.end()) DQ.push(jt->second - kt->first);
		mp.erase(jt); jt = kt;
	}
	it->second = r;//修改一下纵坐标
	if (jt != mp.end()) Q.push(it->second - jt->first);//l 右边的新的拐点
}

int main() {
	cin >> N;
	for (int i = 1; i <= N; ++i) {
		int a; cin >> a;
		pos[a].push_back(i);
	}

	for (int i = 1; i <= N + 1; ++i) mp.insert(make_pair(i, i - 1));
	for (int rep = 1; rep <= N; ++rep) Q.push(-2);

	for (int i = 0; i <= N; ++i) {
		if (pos[i].empty()) ins(1, N);
		else for (int j = 0; j != pos[i].size(); ++j) {
			if (j == 0) {
				if (pos[i][j] > 1) ins(1, pos[i][j] - 1);
			} else {
				if (pos[i][j] - pos[i][j - 1] >= 2) ins(pos[i][j - 1] + 1, pos[i][j] - 1);
			}
			if (j == pos[i].size() - 1 && pos[i][j] < N) ins(pos[i][j] + 1, N); 
		}
		while (!DQ.empty() && DQ.top() == Q.top()) {Q.pop(); DQ.pop();}
		if (Q.empty()) break;
		ans[Q.top() + 3] = i + 1;// Q 维护的是 r-l，实际拐点是 l-1，于是实际f(k)=i 区间右端点是 (r-l)+2
	}
	for (int i = 1; i <= N; ++i) ans[i] = max(ans[i], ans[i - 1]);
	int Q; cin >> Q;
	while (Q--) {int k; cin >> k; cout << ans[k] << '\n';}

	return 0;
}

klein

每个方向的翻转最多只会发生一次，于是可能路径是 $O(1)$ 的。

Day 10 - 7.16

CF1983D Swap Dilemma

key: 无重复序列交换两个数，逆序对数量奇偶性改变。

结论是 A B 可重集相同且逆序对数量奇偶性相同。

证明：

考虑只交换 $(i,i+1)$，显然与原问题等价
可以用若干次操作把 A 换成单增序列，此时 B 的逆序对数量是偶数
令 $l=1,r=2$，对 B 做冒泡排序，因为逆序对是偶数，所以会交换偶数次，相当于 A 没有交换。

习题 CF1591D Yet Another Sorting Problem

CF1628C Grid Xor

构造题，key 是用两个相邻点的结构覆盖矩形，手玩找规律。

大概形如这个样子：


  x x
x o o x
  x x

答案长得就是四边往里堆金字塔，需要分讨 mod 4 的余数。

CF1656E Equal Tree Sums

树上构造题主要从几个方面考虑：

叶子归纳
直径
二分图
度数
重心
$\dots$

子树平衡让人想到根据度数来赋值。

构造：二分图染色后，白点赋 $du[u]$，黑点赋 $-du[u]$。

证明：

每条边两端一白一黑，总贡献 0
删去一个点只会给每个连通块加上 $\pm 1$ 的贡献，仍然相等。

CF1943C Tree Compass

有关树上距离，可以想到直径。

构造：取直径中点，对称染黑（偶数时分讨 mod 4）

证明：直径上点挂的其他链不长于直径上的链，于是一定可以被覆盖到

习题：

CF1736D Equal Binary Subsequences

必要条件：01 个数均为偶数。

连续 01 段长度为偶数的序列是好分的。
把原序列两位一断，00 11 不管，01 和 10 共有偶数个，按 0 1 0 1 ... 地选，循环移位后就消没了。

CF1665D GCD Guess

询问 30 次自然的想到按位确定，构造平凡

还有神奇的 CRT（中国剩余定理）做法，找一组互质的数，枚举余数找到同余关系，CRT 解方程即可。

CF1553F Pairwise Modulo

$p_i=p_{i-1}+\sum a_j \bmod a_i+\sum a_i\bmod a_j$

$a_j\bmod a_i=a_j-\left\lfloor\frac{a_j}{a_i}\right\rfloor a_i$，枚举 $\left\lfloor\frac{a_j}{a_i}\right\rfloor$，权值树状数组直接算。

$a_i\bmod a_j$ 同理，但需要预处理。
对于每个 $a_j$，在 $ka_j$ 上标记一个 $-a_j$，答案就是 $\sum\limits_{x\le a_i} val_x$。

key：调和级数 $\sum \frac{n}{i}=O(n\log n)$

$a_i$ 互不相同，复杂度正确。

CF1548C The Three Little Pigs

q 次询问，给定 x，求 $\sum\limits_{i=1}^n {3i\choose x}$

key：考虑 $3i+1$ 和 $3i+2$

$\left\{ \begin{aligned} &\sum\limits_{l=1}^n \binom{l}{k}=\binom{n+1}{k+1}\\ &\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1} \end{aligned}\right.$

记 $f_{x,j}=\sum\limits_{i=0}^n \binom{3i+j}{x}$

$\left\{ \begin{aligned} &f_{x,0}+f_{x,1}+f_{x,2}={3n+3\choose x+1}\\ &f_{x,1}=f_{x,0}+f_{x-1,0}\\ &f_{x,2}=f_{x,1}+f_{x-1,1}\\ \end{aligned}\right. $

线性 dp 即可。

CF1553G Common Divisor Graph

key1：答案 $\le 2$

$a_i(a_i+1)$ 一定是偶数，故可以 2 步都连到 2

key2：质因子个数 $O(\log n)$ + 质数建中转点

每个质数建新点，每个 $a_i$ 连向质因子，并查集 merge。

答案 $=0$ 就是在同一个并查集里，否则两个并查集只能由一个 $a_i(1+a_i)$ 连接。

枚举 $a_i(1+a_i)$ 的所有质因子对，map 维护连通。
对询问的两个点所在并查集枚举质因子对，check 是否连通。

复杂度 $O(\pi(n)^2)$

CF1689E ANDfinity

先 merge 一遍，得到若干不重复的集合。
发现 lowbit 最大的数 -1 就可以 merge 完所有数。
但是如果出现 1 4 4 4 这种情况，需要再把一个数 +1，变成 101 100 011 就可以了。

CF1617E Christmas Chocolates

发现每次操作相当于保留 lowbit，翻转前面所有。
于是总操作次数上界就是 $\log$ 级别。

对每个 i,k，把 $(i,2^k-i)$ 连边，发现是一棵树，且根据上面的结论，有用的树高是 $\log$ 级别的。
答案等价于求树的直径，可以容易的求出某个数到 0 的距离（暴力跳父亲），然后再求一遍最远点到所有点的距离就行了。

复杂度 $O(n\log V)$

CF1526B I Hate 1111

发现只有 77 777 是有用的，其他都可以用它们表示出来。

由 NOIp 2017 小凯的疑惑可知
key: $\forall (a,b)=1,p,q\in\N$，最大的不能用 $pa+qb$ 表示的数是 $ab-a-b$。

先干掉一个 7，只用 11 111 表示，前面暴力递推，后面直接算等差数列求和即可。

AT_abc232_e [ABC232E] Rook Path

相对于 $(x_2,y_2)$ 只有 4 种位置：不同行不同列，不同行同列，同行不同列，同行同列。

记 $f_{i,j}$ 表示第 i 步走到第 j 种位置的方案数，容易写出转移方程，矩阵乘优化

AT_arc143_e [ARC143E] Reversi

考虑菊花图，一定是先把所有正面朝上的叶子移除，此时若根是正面朝上，移除根，再移除剩下的叶子；否则无解。

启发得到结论：对于一个叶子，若正面朝上，则一定比父亲先被移除，反之亦然。
建边跑拓扑排序即可。

无解情况当且仅当整棵树有偶数个正面朝上的节点。
证明（数归反证）：若有偶数个正面朝上的节点，找到其中一个，它一定有至少一棵子树有奇数个正面朝上的节点，删掉这个点后有偶数个正面朝上的节点。递归下去，最后只剩一个节点，但要有偶数个正面朝上，故这个独点一定反面朝上，无解。

AT_wtf19_d Distinct Boxes

step1：转化条件 $\sum x\le n,\sum y\le m$

step2：希望 $\sum x,\sum y$ 在某种意义下小，赋权重 $p,q$，转化成希望 $p\sum x+q\sum y$ 最小

令 $p+q=10^9+7$（感性理解，p q 范围较大就能更接近有用的情况）。

step3：二分 $K$，把对于每个 $p,q$ 使 $p\sum x+q\sum y$ 最小的 $\sum x,\sum y$ 放到平面上，发现是一个下凸包，要判断 $(n,m)$ 是否在凸包上方。

step4：二分 $p$ 搞出凸包上的点，不断接近 $(n,m)$

step5：二分 $p\sum x+q\sum y \le z$，求出对应的 $\sum x$， $\sum y$，注意到如果选了 $(x,y)$ 则左下方所有点都会选，所以枚举 $n,m$ 较小的那一维，容易求出满足要求的另一维。

复杂度 $O(n^{\frac{1}{3}}\log^3 n)$

Day 11 - 7.17

难度排序 $1<3<2<<4$/kk

what

$n$ 个人有权值 $a_i$，$q$ 次操作：

加入一个权值为 $k$ 的点
全局加 $b$
查询权值 $\equiv y\pmod x$ 的人的数量。

数据范围 $n,q,k,x,y\le 10^5,b\le 10$

key：根号分治

$x\le \sqrt n$ 维护所有答案
$x>\sqrt n$ 枚举所有 $\equiv y \pmod x$ 的数

全局加可以打标记，加入新点减去标记，一定在 $[-1e6,1e5]$ 之间，直接开桶维护即可。

复杂度 $O(n\sqrt n)$

HNOI2003 年份

给定数字串 $s$，给出划分（允许有前导 0）满足：

数值严格递增
最后一个数尽量小的前提下，字典序尽量大

数据范围 $\sum |s|\le 2\times 10^6$

错误想法：二分 + 贪心
有时我们会“牺牲”一些后面的数，让前面的数更大，从而字典序更大

字典序大和单增是矛盾的，需要找到平衡，而 dp 就是干这个的。

key：双向 dp + hash 子串比较 + 线段树优化决策

设 $f_i$ 表示 $s[1\dots i]$ 最后一段合法的最大起点，$g_i$ 表示 $s[i\dots n]$ 第一段合法的最大终点。

这样我们正着推一遍 $f_i$，以 $g_{f_n}=n$ 为起点反着推一遍 $g_i$，就可以得到最后一段最小的前提下，字典序最大的方案。

$\begin{aligned} f_i&=\max\limits_{1\le j\le i}\{j, {\rm num}(f_{j-1},j-1)<{\rm num}(j,i)\}\\ g_i&=\max\limits_{i\le j<n}\{j, {\rm num}(i,j)<{\rm num}(j+1,g_{j+1})\}\\ \end{aligned}$

子串比较可以用 hash 二分求 lcp 优化到 $\log$

另外，这两个式子满足决策单调性，即值单调递增。

考虑 $f_i$ 对后续 dp 的贡献，发现满足 ${\rm num}(f_i,i)\le {\rm num}(i+1,j)$ 的 $j$ 是一段后缀，于是可以用区间取 max，单点查询的线段树维护。$g_i$ 同理。

由于是单点查询，标记可以永久化，不需要上下传，减少常数。
注意多测清空不可以用 memset

au

定义广义菊花图：

只有一个重心
以重心为根，所有点的深度不超过 3
深度为 2 的点至少 $\left\lfloor \frac{n}{2} \right \rfloor$ 个
所有深度为 2 的点，子树大小不超过 $\left \lceil \frac{n}{4} \right \rceil$

问 $n$ 个点的有标号广义菊花图的数量，答案对 $P$ 取模（不保证 $P$ 为质数）

数据范围 $n\le 5000$

简单计数题，分层考虑。

根节点只有 1 个，n 种情况
设第二层有 $x$ 个节点，${n-1}\choose x$ 种情况
第三层考虑容斥
- 若没有限制，有 $x^{n-x-1}$ 种情况（每个点随便选父亲）
- 若不合法，有且仅有一棵子树有 $y> \left \lceil \frac {n}{4}\right \rceil$ ，有 $x{{n-x-1}\choose {y-1}} \times (x-1)^{n-x-y}$ 种情况（先选不合法子树，其他叶子随便选父亲）。

预处理组合数和幂次，复杂度 $O(n^2)$

WC2024 镜像

给定 $h_i$，定义一个二元组 $(u,v)$ 是“好的”当且仅当：

存在一个正实数 $L$，使得存在一个单增序列 $r_u,\dots ,r_v$，满足 $r_i\in\{h_i,2L-h_i\}$

求“好的”二元组个数。

f1：线段树分治 + 可撤销并查集

枚举 T，找最大合法 $(u,v)$

考虑如果知道 $L$，那么我们可以 $f(i,0/1)$ dp。
认为我们是在两行点上做，于是我们希望知道这个图的连通性。
注意到某条边是否联通（某个转移能否实现）只取决于 $2L$ 和 $h_i+h_{i+1}$ 的大小关系，于是本质不同的 $L$ 只有 $O(n)$ 个。

另外注意到对于某个 $u$，合法的 $v$ 是一段区间，故要求的就是最大右端点。

我们可以从小到大枚举 $L$，维护当前的连通块。每新合并出连通块 $[l,r]$，$\forall u\in[l,r]$ 可达的右端点与 $r$ 取 max，最终就可以得到对每个左端点，合法的区间数量。

某条边的存在条件对应 $L$ 的一段区间，于是我们需要维护支持加减边的动态图连通性，但不要求在线。

可撤销并查集：不进行路径压缩，通过启发式合并保证树高 $\log$ 级。因为需要维护子树大小，只能按照加入顺序从后到前删边

线段树分治：把修改、询问挂在时间轴上，从根节点往下遍历，把经过的标记都修改掉，从儿子回到父亲的时候撤销修改

线段树分治 + 可撤销并查集是非常经典的用法，因为线段树分治保证了撤销是从后到前的

f2：矛盾情况 $\to$ 合法区间

枚举 $(u,v)$，考虑是否存在合法 $T$

令 $T=2L$，发现对于一些 $h_i,h_{i+1},T$ 的关系，会决定 $r_i,r_{i+1}$ 的取值。

因为 $r_i$ 不可能既取 $h_i$ 又取 $T-h_i$（除非 $2h_i=T$），于是会有 3 种矛盾：

$h_i=h_{i+1}$ 且 $h_i+h_{i+1}=T$
$h_{i-1}\le h_i$ 且 $h_{i-1}+h_i\le T$，$h_i \ge h_{i+1}$ 且 $h_i+h_{i+1}\ge T$
$h_{i-1}\ge h_i$ 且 $h_{i-1}+h_i\ge T$，$h_i \le h_{i+1}$ 且 $h_i+h_{i+1}\le T$

考虑后两种情况相当于如果存在 $h_{i-1}\le h_i\ge h_{i+1}$ 或反过来，就会对 $T$ 的取值有 $\in(l_i,r_i)$ 的限制。

那么合法当且仅当这些区间的交不是空集，因为若区间交非空，那么 $T$ 有无数种取值，可以避开第一种矛盾。

求区间交相当于求 $\max l_i < \min r_i$。

显然当 $u$ 增加时，$v$ 的最大值单调不降，故可以双指针扫。

预处理 $l_i$ $r_i$，st 表 check，复杂度 $O(n\log n)$。

Day 12 - 7.18

name

给定 $n$ 个模式串 $s_i$，构造最短的包括所有模式串的文本串。

数据范围 $n\le 20,|s_i|\le 5\times 10^4$

key: hash 预处理 + 状压 dp

状压 dp 是显然的，关键在预处理包含和前后重叠。

hash 是判断字符串相等的重要工具，尤其是有很多子串的时候/kk（要记住啊/kk

可以二分 + hash 或者直接暴力，复杂度是对的。

注意有很多相同字符串的时候要保留一个，不能都删掉。

chk

$n$ 个点的无向完全图，$k$ 棵生成树 $T_k$，两个要求：

每条边最多出现在一棵生成树中
对于任意一组 $u,v$，在任意两棵生成树上，$u\to v$ 的路径除 $u,v$ 外没有相同节点。

给出 $k$ 棵生成树，判断是否满足这两个要求。

数据范围 $k\le n\le 600$

key：$u\to v$ 在 $k$ 棵生成树上最多有 $n$ 个不同节点

因为如果跳到相同的就寄了，如果跳不到就最多只会跳 n 次，于是枚举 $u,v$，复杂度是 $O(n^3)$

tree

定义和 t2 相同，要求构造 $k$ 棵生成树

满足第一个要求，且不满足第二个要求
同时满足两个要求

找到一棵合法的，然后转一圈。

第 1 种好构造，就是在圆上左右跳，一定没有重边

注意到 $k\le \frac{n}{2}$，而我们显然希望路径上的点尽量少，也就是希望图尽量扁。

菊花图是不行的，因为边不能重复，这样会让一个点变成独点。

但是把两个菊花图拼起来就可以了。

我们让 $i,i+\frac{n}{2}$ 当两个根，中间的点分别接到两个根上，发现路径只会经过根，而根是不重复的，于是路径是不交的。

grid

支持加减边，在线维护 2 行 $m$ 列的网格图连通性。

数据范围 $m,q\le 10^5$

key：线段树维护区间四个端点的连通性

合并平凡，查询注意 $(l,1) (l,2)$ 可以从左边绕着连通，于是要先查询 $(1,l) (r,n)$ 再更新一下 $(l,r)$ 的答案。

Day 13 - 7.19

CF1404E Bricks

给定 $n\times m$ 的网格，每个格子必须被覆盖或必须不被覆盖。用长为 1，宽为任意长度或宽为 1，长为任意长度的长方形覆盖，要求不能重叠，求最少用几个长方形。

数据范围 $n,m\le 200$

key：边点转化 + 二分图最大独立集

认为我们用大于 $1\times 1 $ 的长方形覆盖相当于擦除内部的边，而覆盖不重叠等价于每个格子相邻的边不能同时被擦除。

把能擦除的网格边建点，不能同时被擦掉的点建边，求二分图最大独立集。

大概就长成这个样子：

CF1482H Exam

给定若干字符串 $s_i$，计数有序二元组 $(i,j)$ 满足：

$i!=j$
$s_j$ 是 $s_i$ 的子串
不存在 $k\not=i,j$ 使得 $s_j$ 是 $s_k$ 的子串，且 $s_k$ 是 $s_i$ 的子串。

数据范围 $\sum |s_i|\le 10^6$

key：AC 自动机 fail 树

固定 $i$，统计合法的 $j$。

考虑没有第 3 个限制。

$s_j$ 是 $s_i$ 的子串当且仅当 fail 树上 $s_j$ 的 end 是 $s_i$ 某个节点的祖先。

显然子串等价于“某个前缀的后缀”

于是建出 $fail$ 树，统计 $s_i$ 每个节点到根的路径并上，end 节点的数量即可。

实现可以倍增 + 树上差分 / 树剖，合并 $s_i$ 的节点时，向 lca 打标记（贡献 +1），最后统计一遍即可。

. . . . . . . . . . . . . . . . . . . . . . . .

考虑增加第 3 个限制，相当于只有 fail 树上最近的 end 可能产生贡献，先把这些答案串拿出来。

对一个答案串，我们希望知道它是不是某个答案串的子串，也就是希望知道它的子树内是否有某个答案串的前缀。

从后到前扫描 $s_i$，把以每个位置为终点的，最长的答案串的前缀塞进 set 里，check dfn 即可。

P3236 [HNOI2014] 画框

给定一个完全二分图，每条边有权值 $a_{i,j},b_{i,j}$，求一个完美匹配，最小化 $(\sum\limits_{(i,j)\in \rm E} a_{i,j})(\sum\limits_{(i,j)\in \rm E} b_{i,j})$

数据范围 $T\le 3,n\le 70,a_{i,j},b_{i,j}\le 200$

类似 devans 讲的 AT_wtf19_d Distinct Boxes 这道题，我们希望 $\sum a_{i,j}$ 和 $\sum b_{i,j} $ 在某种意义下小，但我们需要牺牲一些较小值来保持“平衡”，于是把二维通过赋权重转成一维。

考虑把二维决策扔到平面上，不妨横坐标 $\sum a_{i,j}$ 纵坐标 $\sum b_{i,j}$，$maxans=(\sum a_{i,j}) (\sum b_{i,j})$ 是一个反比例函数，显然 $\min \sum a_{i,j} $ 和 $\min\sum b_{i,j} $ 对应的点 $A,B$ 在这个反比例函数的上方，而把所有可能的点放在平面上后，最终答案一定在下凸包上，即在直线 AB 下方。

分治求凸包上的点，考虑找距离直线 AB 最远的点 C，保证分治 AC BC 后凸包上的点在 AC BC 下方。

记直线 AB 为 $Ax+By=C$，要求使 $Ax+By$ 的值最小的一组 $(x,y)$，那么我们直接把边权设成 $Aa_{i,j}+Bb_{i,j}$，KM 跑二分图最小权完美匹配。

可以证明值域 $[0,n]$ 的整点凸包点数在 $n^{\frac {2}{3}}$ 量级

P7880 [Ynoi2006] rldcot

给定 $n$ 个点的边带权树，$m$ 次询问 $[l,r]$，求满足 $l\le i,j\le r$ 的 $dep(lca(i,j))$ 有多少种取值（$i,j$ 可以相同）。

数据范围 $n\le 10^5,m\le 5\times 10^5,w\in [-10^9,10^9]$

考虑一个点会在什么时候产生贡献，显然是左右儿子都有 $[l,r]$ 内部节点的时候。

把子树内节点按编号排成一列，形如：o o # # o # o # #，发现只有相邻的才有用，因为如果不相邻的都在区间内，那么相邻的肯定也在区间内。

相邻节点可以贡献答案的区间要求形如 $l\le L<R\le r$，显然是一个矩形，可以扫描线做。

找相邻点对的过程使用启发式合并，复杂度正确。

Day 14 - 7.20

network

毒瘤题。

给定 $n$ 点 $m$ 边的无向图，要求给每个点赋权值 ${a_i,b_i}$ 满足：

$a_i<b_i$
$i\not=j,\{a_i,b_i\}\not=\{a_j,b_j\}$
$i\not=j,|\{a_i,b_i\}\cap\{a_j,b_j\}|= 1$ 当且仅当 存在边 $(i,j)$

数据范围 $\sum n\le 10^6,\sum m\le 10^7$ 10s

alt text

walk

傻子题，与 palacinke 几乎完全相同，甚至弱于这道题

key：容斥 + 矩阵乘

data

给定 $n$ 个点的有根树，有 2 种物品，每个点必须选其中一种机器，分别获得 $g_i=r_{i,0/1}$ 的满意度。
定义 $f_i=\left\lceil\frac {x_i}{1000}\right\rceil\times 666\times i$，其中 $x_i$ 代表 $i$ 及儿子满意度 $g$ 的极差。
最大化 $\sum g_i-f_i$。

数据范围 $n\le 10^5,r_{i,0/1}\le 10^5$

key: 枚举 $\left\lceil\frac {x_i}{1000}\right\rceil$ 只有 $101$ 种取值

我们希望知道 $i$ 的儿子集合能否满足极差 $\le x_i$ 的条件，可以把所有值扔到数轴上，双指针推区间 $[l,r]$，判断能否覆盖所有儿子，同时维护子树和最大值，更新答案。

const int N=1e5+5;
vector<int> e[N];
#define pb push_back
const LL INF=1e18;
int n;
LL f[N][2];int rp[N][2];
struct node{
    int id,p;LL val;int op;
    node(int id=0,int p=0,LL val=0,int op=0):
        id(id),p(p),val(val),op(op){}
    bool operator<(const node &b) const{
        return p<b.p;
    }
};
vector<node> vec;
bool in[N][2];
int siz,tot;LL ans;

inline void add(node x){
    in[x.id][x.op]=1;
    if(!in[x.id][x.op^1]) ans+=x.val,tot++;
    else if(f[x.id][x.op]>f[x.id][x.op^1])
        ans+=f[x.id][x.op]-f[x.id][x.op^1];
}
inline void del(node x){
    in[x.id][x.op]=0;
    if(!in[x.id][x.op^1])ans-=x.val,tot--;
    else if(f[x.id][x.op]>f[x.id][x.op^1]) 
        ans-=f[x.id][x.op]-f[x.id][x.op^1];
}

inline LL ff(int xi,int u){return (LL)(xi+999)/1000*666*u;}
inline void calc(int u,int op,int xi){
    tot=0;ans=0;int r=-1;
    rep(l,0,siz-1){
        while(r+1<siz && vec[r+1].p-vec[l].p<=xi) add(vec[r+1]),r++;
        if(tot==(siz+1)/2) f[u][op]=max(f[u][op],ans-ff(xi,u)); 
        del(vec[l]);
    }
}
inline void solve(int u,int op){
    vec.clear();
    vec.pb(node(u,rp[u][op],rp[u][op],op));
    for(auto v:e[u]){
        vec.pb(node(v,rp[v][0],f[v][0],0));
        vec.pb(node(v,rp[v][1],f[v][1],1));
    }
    sort(vec.begin(),vec.end());
    siz=vec.size();
    int mx=vec.back().p-vec.front().p;
    for(int xi=0;xi<=mx+1000;xi+=1000) calc(u,op,xi);
}

inline void dfs(int u){
    if(e[u].empty()){
        f[u][0]=rp[u][0],f[u][1]=rp[u][1];
        return ;
    }
    for(auto v:e[u]) dfs(v);
    solve(u,0);solve(u,1);
}

Day 16 - 7.22

平均分成两部分，这个限制非常像二分图。

序列内相邻位置连边，每个值出现顺序相邻连边，显然两种边分别内部不会相连，于是不存在奇环。

CF1638D Big Brush

key：最后一次操作一定留下一个 $2\times 2$

倒着从后往前 bfs 即可。

CF1630D Flipping Range

key1：所有 $b_i$ 可以规约成 $k=1$

辗转相减，最后剩下的就是 ${\rm gcd} \{b_i\}$ ，且因为 $b_i\le \frac{n}{2}$ 所以一定可以。

key2：考虑 $\bmod b$ 同余的位置

显然我们可以同时翻转相隔 $b$ 的位置，方法就是操作连续两个区间，这样中间的都覆盖完了。

于是按 $\bmod b$ 分类，容易发现每次操作不改变每类内负数个数的奇偶性。于是如果偶数个，那么可以全变成正数，否则把绝对值最小的变成负数即可。

但是会存在若干反例，如 $n=6,b=3$ -9 -9 -9 1 1 1，此时翻转 $[1,b]$ 就可以改变每类负数个数的奇偶性，两种取 $\max$。

CF1712E2 LCM Sum (hard version)

${\rm lcm}(i,j,k) < i+j+k$ 是非常严格的条件。

考虑去掉 $\rm lcm$ ，记 $i=\frac {\rm lcm}{a}$，$j=\frac {\rm lcm}{b}$，$k=\frac {\rm lcm}{c}$，条件转化为 $\frac{1}{a}+\frac{1}{b}+\frac{1}{c} > 1$。

显然正整数解只有 3 种：

$c=1$
$a=4,b=3, c=2$
$a=5, b=3 ,c=2$

后两种直接枚举 $k$ 统计一下就行。
关键在维护 $[l,r]$ 内 $k$ 的因数个数及组合数。

key：离线 + 倒着枚举倍数

考虑所有数不相同，枚举倍数是 $O(n\log n)$ 的调和级数。
从大到小枚举倍数，维护组合数，在左端点处理询问，直接区间求和即可。

CF1798F Gifts from Grandfather Ahmed

key：EGZ 定理

任意 $2n-1$ 个数，都能选出 $n$ 个数，满足它们的和是 $n$ 的倍数

按 $s_i$ 从小到大依次 dp 构造即可。

CF1442C Graph Transpositions

key：分层图 + 按答案大小分治

显然，在图上单纯走边最多走 $O(m)$ 条，而翻转操作代价增长是指数级的。

如果翻转次数 $\le 20 $，就有可能通过翻转操作减少走的边数；但如果翻转操作很多，单纯走边无法抵消翻转，此时显然希望翻转越少越好。

于是对前 20 次翻转建分层图，在图上跑最短路。
对翻转次数多的，直接建一个正图一个反图，层间连边权 1e9，这样就会尽量少翻转，最后最短路除 1e9 就知道翻转了多少次。

两种答案取最小值即可。

CF1830D Mex Tree

key：树上 dp + 答案下界优化状态

首先 mex 只有 $0/1/2$ 三种，而我们只关心 $0/1$，也就是路径上全 $0/1$ 的。

考虑 $O(n^2)$ dp，设 $f(u,0/1,i)$ 表示 $u$ 是 $0/1$，子树内与 $u$ 相连的同色连通块大小是 $i$，答案的最大值。枚举子树转移，实现平凡。

发现有一种显然的较优构造是 01 染色，答案大概是 $n^2-O(n)$ 级别，于是同色连通块大小不能超过 $O(\sqrt n)$，否则一定不优。

这样就能把背包的第三维优化到 $\sqrt n$，时间复杂度 $O(n\sqrt n)$

CF1794E Labeling the Tree with Distances

key：hash判可重集相同 + 换根

条件等价于以 x 为根，所有点深度的可重集与给定的权值集合相同，但允许有一个自选。看上去很奇怪，但是深度 $\le n$ 所以可以直接枚举自己选的是什么数。

判断可重集相同最常用的就是哈希，常见的好维护的哈希方式是 $\sum cnt_i\times p^i$（这同样可以用来做 NOI2024 D1T1）。

用换根 dp 维护子树内和子树外的哈希值，转移平凡。

CF1733E Conveyor

看上去是找规律但它其实是 dp /kk

发现经过某个格子的 slime 一定是向右/向下交替，即若有 $n$ 个 slime 经过，那么 $\left\lceil \frac{n}{2}\right \rceil$ 向右， $\left \lfloor \frac{n}{2}\right\rfloor$ 向下。

于是我们就可以从左上角开始递推出到过每个格子的 slime 数量。

求时间 $t$ 格子上有没有 slime，等价于看前 $t-1$ 秒经过格子的 slime 数量，与前 $t$ 秒经过的是否差 1。

求前 $t$ 秒到 $(x,y)$ 格子的 slime 数量，从 $f(0,0)=t-x-y+1$ 开始递推到 $f(x,y)$。
为什么是 $t-x-y+1$？因为最后出发的来不及到达 $(x,y)$ 所在的对角线，不会产生贡献。

CF1768E Partial Sorting

key1：$f(p)\le 3$

前 $2n$ 个排一遍，后 $2n$ 个排一遍，前 $2n$ 个再排一遍，一定全都排好。

$f(p)\le 0$：已经排好序了，共 $1$ 种
$f(p)\le 1$：前 $n$ 个/后 $n$ 个已经排好，共 $2(2n)!-n!$ 种
$f(p)\le 2$：$[1,n]$ 在前 $2n$ 个里/ $[2n+1,3n]$ 在后 $2n$ 个里
$f(p)\le 3$：全部，$(3n)!$ 种

关键在算 $f(p)\le 2$，发现直接 $2{2n\choose n}(2n)!$ 会算重两个条件都满足的情况。

key2：枚举中间 $n$ 个的情况去重

设 $[1,n]$ 有 x 个在中间 $n$ 个里，我们要在前 $n$ 个里选 $n-x$ 个给 $[1,n]$，再在后面的 $2n-x$ 个里选 $n$ 个给 $[2n+1,3n]$，剩下位置填 $[n+1,2n]$。

写成式子就是 $\sum\limits_{x=0}^{n} {n\choose x}{n\choose n-x}{2n-x \choose n}(n!)^3$

于是 $f(p)\le 2$ 的有 $2{2n\choose n}(2n)!-\sum\limits_{x=0}^{n} {n\choose x}{n\choose n-x}{2n-x \choose n}(n!)^3$ 种

Day 17 - 7.23

太不好了，这么多签到题（敲打
好像有点不敢想了呢/kk
不应该这样的，正解是要努力想努力写的/kk

dream

$n$ 个点的根为 1 的树，每个点有权值 $a_i,b_i,c_i$，对于每个点 $x$，求 $\max\limits_{u,v\in T(x),u\not=v,|dep_u-dep_v|\le k} a_{lca(u,v)}b_uc_v$。其中 $T(x)$ 表示点 $x$ 的子树。

数据范围 $n\le 2\times 10^6,k\le 63$

key：树上启发式合并

$O(n\log n\log D)$ 重链剖分 + 线段树

线段树维护 $dep_j=i$ 的 $b_j,c_j$ 最大值，遍历轻子树更新答案。

理论复杂度是与 $D=\max dep_i$ 有关的，而这一项与轻子树大小总和呈现一种类似反比例的关系，于是总复杂度大约就是 $O(n\log n)$ 带一个略大的常数。

实测需要 3.5 - 4.5 s，也就是说比正解多了一个 2 左右的常数，差不多就是 $\log n$ 和 $\log k$ 的区别。
不过我的线段树实现不算很快，实现好一点的话可能卡进 2s。

$O(n\log k)$ 长链剖分 + ST 表

发现前面这种做法的瓶颈在遍历轻子树，而我们这道题其实不太关注 size，反而与深度息息相关。

使用长链剖分，st 表维护距离点 x 在 $[d,d+2^i-1]$ 区间的 $b,c$ 的最大值，这样对于每个轻儿子，我们不需遍历整棵子树，只需要处理 $O(长链)$ 的信息。

st 表使单次插入和修改均摊复杂度为 $O(\log k)$，而每次合并相当于删除这条长链，每个点只会被删除一次，故总复杂度是 $O(n\log k)$ 的。

travel

一棵无限大的完美二叉树（$i$ 的儿子是 $2*i$ 和 $2*i+1$），无限远向 1 连边。每次树上游走，除了起点和终点外，只能在对偶图上走。若干次询问从 $a$ 到 $b$，至少要横穿多少条树边。

数据范围 $T\le 10^4,a,b\le 10^8$

显然是按位跳，复杂度 $O(T\log a)$ 。

令一个平面对应它正上方的点。

发现一定是往 lca 的下面/左边/右边跳，分别计算三种的答案。

每次穿过一条树边一定是往相邻的左/右平面跳，可以计算这个平面对应的点。从而可以计算从一个点向上跳到某个平面，穿过的边的个数。（注意，在同一棵子树内，显然是往编号更小的平面跳更优）

LL LCA(LL a,LL b){
	if(a<b) swap(a,b);
	while(floor(log2(a))>floor(log2(b))) a>>=1;
	per(i,63,0) if((a>>i)!=(b>>i)) return a>>(i+1);
	return a;
}
LL left(LL a){
	return a>>__builtin_ffs(a);
}
LL right(LL a){
	if(__builtin_popcount(a+1)==1) return -1;
	return left(a+1);
}
bool in(LL a,LL b){
	if(a==0 && b==-1) return 0;
	if(a==-1 && b==0) return 0;
	if(b==-1 || b==0) return 1;
	rep(i,0,63) if((a>>i)==b) return 1;
	return 0;
}
int jump(LL a,LL b){
	if(a==b) return 0;
	int res=-1;//first step no cross
	
	while(a!=b){
		LL L=left(a),R=right(a),nxt=LONG_LONG_MAX;
		if(in(L,b)) nxt=min(nxt,L);
		if(in(R,b)) nxt=min(nxt,R);
		a=nxt;res++;
	}
	return res;
}
void work(){
	LL c=LCA(a,b);
	int u1=jump(a,c),u2=jump(a,left(c)),u3=jump(a,right(c));
	int v1=jump(b,c),v2=jump(b,left(c)),v3=jump(b,right(c));
	int ans=min({u1+v1,u1+v2+1,u1+v3+1,u2+v2,u2+v1+1,u2+v3+1,u3+v3,u3+v1+1,u3+v2+1});
	printf("%d\n",ans);
}

runplus

$n$ 个点的边带权树，每天每个点上会出现 $c_i$ 个人。每天会有 $num_i$ 个打卡点，每个人要往最近的打卡点跑。在线求每天所有人跑步的距离和。

数据范围 $n\le 2\times 10^5,\sum num_i\le 6\times 10^5$

显然需要与 $\sum num_i$ 相关的算法，考虑把所有关键点取出来。

key：虚树上统计答案

虚树上的点可以直接跑多源 bfs 求最短路

实树上的点分为两类：

虚树节点的实子树
虚树边上点的实子树

实树上的点一定是先到虚树上，再到最近的打卡点。
虚树节点的贡献容易计算，边上参考链需要二分出向上/向下跑的分界点，预处理一大堆东西统计答案即可。

fight

给定多项式 $a_n$, $b_m$，$q$ 次询问 $a,b$ 卷积 $l\dots r$ 项的系数和。

数据范围 $n,m\le 2\times 10^6,q\le 25$

全场最大诈骗题！

本质就是求 $\sum \limits_{i+j\le x} a_ib_j$，这个式子显然可以枚举 $i$，预处理 $b_i$ 前缀和优化到 $O(n)$，而 $[l,r]$ 的答案就是 $f(r)-f(l-1)$。

Day 18 - 7.24

merge

给定序列 $a_n$，可以若干次操作：

合并 $a_i$ 和 $a_{i+1}$ 为 $a_i+a_{i+1}$

求至少多少次操作，能把序列变成回文的。

key：双向贪心

mahjong

题面太长，不想写了。

key：dp预处理

只关心一共有几种关键牌，有没有一对，还剩多少张牌。直接 dp 转移即可。

build

给定序列 $a_n$，初始 $h_i=0$，每次操作：

选择区间 $[l,r]$ 和 正整数 $x$，对 $\forall i\in [l,r],h[i]\leftarrow h[i]+x$

求最少需要几次操作，使得 $h=a$

数据范围：$n\le 18,T\le 100$

转化成从 $a_i$ 往下减。

key1：区间加减想差分
在 $a_i$ 的差分数组 $d_i$ 上操作，转化为 $d_l - x$，$d_{r+1}+x$，最终要让所有 $d_i$ 变成 $0$。

key2：能找到一种最佳方案，每次操作让一个 $d_i$ 变成 $0$
对于每次操作，连边 $(l,r+1)$，显然会连出一个森林。其中每棵树内部可以转化成从小到大依次满足，于是一棵树合法的充要条件是 $d_i$ 的前缀和 $\ge 0$。
记 $f_S$ 为把 $S$ 中的 $d_i$ 都变成 $0$ 需要的最少次数，枚举子集转移即可，复杂度 $O(3^n)$

count

给定一棵 $n$ 点无根树和排列 $p_n$。对 $rt=1,2,3,\dots,n$，求 $\sum\limits_{1\le l\le r\le n} h(l,r)$，其中 $h(l,r)$ 为 $p_l,p_{l+1},\dots,p_r$ 的 $\rm lca$ 的编号。

数据范围 $n\le 2\times 10^5$

key：树上启发式合并 + 换根

转化为求对每个 $x$，有多少区间满足所有点都在 $x$ 子树内，这可以用启发式合并 + set 简单求出（每次插入一个点，合并区间）

结合换根，需要求一个子树内的答案和一个子树外的答案，推推式子即可。

Day 20 - 7.26

P4494 [HAOI2018] 反色游戏

一张 $n$ 个点 $m$ 条边的无向图，初始每个点有黑白两色，每条边可以选择是否操作，如果操作这条边连接的两个点都会反色。
问有多少种选择方案使得最后点都是白色的。对每个点删除这个点以及与其相连的边之后询问。

数据范围 $n,m\le10^5$

有解的充要条件：每个连通块异或和均为 0

视黑色为 $1$，白色为 $0$，每次操作不改变异或和。
随便找一棵生成树，从叶子开始依次确定，最后由于异或和为 0，根一定满足要求。
那么生成树外的边就可以随便操作，方案数是 $2^{m-n-cnt}$，其中 $cnt$ 是连通块数量。
求点双维护连通块数量即可。

P7099 [yLOI2020] 灼

桃之夭夭，灼灼其华

一个数轴，有 $n$ 个关键点：$x_1,x_2,\dots,x_n$。
$Q$ 次询问，每次给出一个初始位置，然后每轮等概率向左或向右移动，遇到关键点终止。
问期望经过的轮次数

数据范围：$q\le 5\times 10^6,x_i\le 10^9$

显然 $n$ 个点是没用的，有用的是每次询问两边的点，不妨记为 $[0,m]$。

可以写出式子 $f_i=\frac{1}{2}(f_{i-1}+f_{i+1})+1$
变形成递推式 $f_{i+1}=2f_i-f_{i-1}-2$，设 $f_1=x$，就可以递推出 $f_m=kx+b$，又知道 $f_0=f_m=0$，就可以解出 $x$ 从而得到答案。
矩阵快速幂优化是会 T 的，需要预处理 $[1,\sqrt x_i]$ 和 $2\sqrt x_i,3\sqrt x_i,\dots,x_i$ 的矩阵值，$O(1)$ 回答询问。

另解：变形成 $(f_{i+1}-f_i)=(f_i-f_{i-1})-2$，即可累和推出通项公式，不需预处理即可 $O(1)$ 计算答案。

P3679 [CERC2016] 二分毯 Bipartite Blanket

给定一个二分图，两边分别有 $n,m$ 个点，每个点有点权，给定 $t$，求多少点集满足点权和 $\le t$ 且能被一个匹配覆盖。

数据范围 $n,m\le 20$

key1：考虑只有一边——hall定理

点集 S 可以被一个匹配覆盖，当且仅当：
$\forall T\subseteq S$，与 $T$ 内点有边相连的点集不小于 $T$

key2：两边分别可以被覆盖，则整体可以被覆盖

证明：
将左部点和右部点对应匹配取并，每个点度数不超过 2，即只存在环或链。
环和长度为奇数的链是容易的，直接隔一个取一个。
长度为偶数的链一定有一个端点不在点集里，否则左部和右部点数量不相同，去掉这个端点就是长度为奇数的链了。

左右分别枚举点集判断能否被覆盖，最后排序双指针统计答案。

P5287 [HNOI2019] JOJO

一个初始为空的字符串，每次可以在后面添加一些相同的字符，或者回退到某个先前状态，求每次得到的字符串的kmp的next数组每位之和。

数据范围：询问 $\le 10^5$，每次加入 $\le 10^4$

第一想法是直接跳 next 找与新加入字符相同的段，但这样复杂度是字符集均摊的，会被卡掉。

考虑优化跳 next 的过程，发现如果每次跳的很短那么一定是有循环节，而直接跳过所有循环节是不会有问题的。如此，每次跳 next 长度至少减半，复杂度就是严格 $\log$ 的。

离线询问建出类似 trie 树的东西，直接递推求即可。

P6729 [WC2020] 有根树

给定一棵 $n$ 个点的树以及 $q$ 次操作。维护一个初始为空的点集 $S$，每次加入一个点或者去掉一个点。
对于一个点 $i$ 定义 $size_i$ 为 $i$ 子树内 $S$ 点集内的点数。对于树上一个连通块 $C$，定义其权值为 $\max\{size_i,i\not\in C\}$ 和 $|C\cap S|$ 的最大值。
询问每次修改完所有可能连通块权值最小值。

数据范围 $n\le 5\times 10^5,q\le 10^6$

首先 $C$ 一定是树顶 size 最大的一部分

key：每次操作答案最多 $\pm 1$

记 $X=\max\{size_i,i\not\in C\}$，$Y=|C\cap S|$，显然可以令 $X\le Y$。

加入一个点影响是路径 +1，可能导致 $X>Y$，此时需要把 $X$ 的最大值点吞掉，并可能把 $C$ 内部 size 最小的点（$<x$）扔出去。
删除同理，最终答案变化不会超过 1

一个简单的想法就是用树剖 + 线段树维护 size，复杂度 $O(q\log^2n)$

. . . . . . . . . . . .

考虑对于每一条重链，最多只会有1个位置，两侧的点一个在连通块内一个在连通块外。
记录所有重链上这两个点，若都在 $C$ 内或 $C$ 外时，只有一个点。
用链表对每一种 $size$ 维护上面两种点，加入或删除的时候会对 $\log n$ 条重链进行加减操作，操作 $O(\log n)$ 个点。调整答案时从链表中找到更改的位置，用set对每条重链维护连通块内外的点。复杂度 $O(n\log n)$。

UOJ 513

给定 $n$ 个点 $m$ 条边带 01 边权的无向图，两种操作：

对一个简单环 $\rm xor 1$
将点集分成两份并对介于两者之间的边 $\rm xor 1$
询问能否在 $m+1$ 次操作内将边权清 0

数据范围 $n\le 300,m\le \frac{n(n-1)}{2}$

key：看到简单环想生成树

任意环操作一定可以转换成若干非树边对应环的操作。
每次操作不改变节点度数奇偶性，于是若所有点度数都是偶数，则可以用不超过 $m-n+1$ 次操作完成。

第二种操作可以转化成单点操作，一共 $n$ 种。
要求解异或方程组，使用线性基即可。

UOJ 574

$n\times m$ 的灯阵，每盏灯将在 $[0,1]$ 之间独立均匀随机的时间 $p$ 之后亮起。
对于一个时刻，如果恰好有 $x_i$ 行，$y_i$ 列灯光全部亮起，设亮起的灯光总数为 $k$，可以节省 $F_k$ 的电量。$F_k$ 为斐波那契数列第 $k$ 位。共有 $h$ 对 $(x_i,y_i)$。
求节省电量期望 $\bmod 998244353$ 的结果

数据范围 $nm,h\le 5\times 10^5$

key1：第 $k$ 盏灯期望在 $\frac{k}{nm+1}$ 秒后亮起

\[E_k=nm\int_{0}^{1} x\cdot x^{k-1}(1-x)^{nm-k} dx \]

具体我也不会算，反正是对的

key2：容斥 + FFT

对于 $k$ 个灯亮起的情况，满足 $(x,y)$ 条件的方案数是：

\[\sum \binom{n}{i}\binom{m}{j}\binom{(n-i)(m-j)}{nm-k}(-1)^{i-x}(-1)^{j-y}\binom{i}{x}\binom{j}{y} \]

说是可以拆开组合数然后卷积/kk

posted @ 2024-07-12 17:36 Cindy_Li 阅读(170) 评论(0) 收藏举报

刷新页面返回顶部

于暗夜中，守一束光