李超线段树

李超线段树

用于维护平面上的一次函数，支持在线插入 & 求单点最大值（编号）

---

插入

现在要加入一个一次函数 \(f(x)=kx+b\)，定义域 \([s,t]\)。

注意：当线段垂直于 x 轴时，应插入定义域为 \([x,x]\) 的一次函数 \(f(x)=0\cdot x+y_1\)

考虑某个被 \(f\) 完全覆盖的节点 \(x\)，区间 \([l,r]\)

标记 \(tg[x]\) 代表可更新本区间超过一半的线段编号

1. 如果该区间还没有标记，直接标记为 \(f\) 即可
2. 如果已经有标记了，根据定义，需要分类下传标记

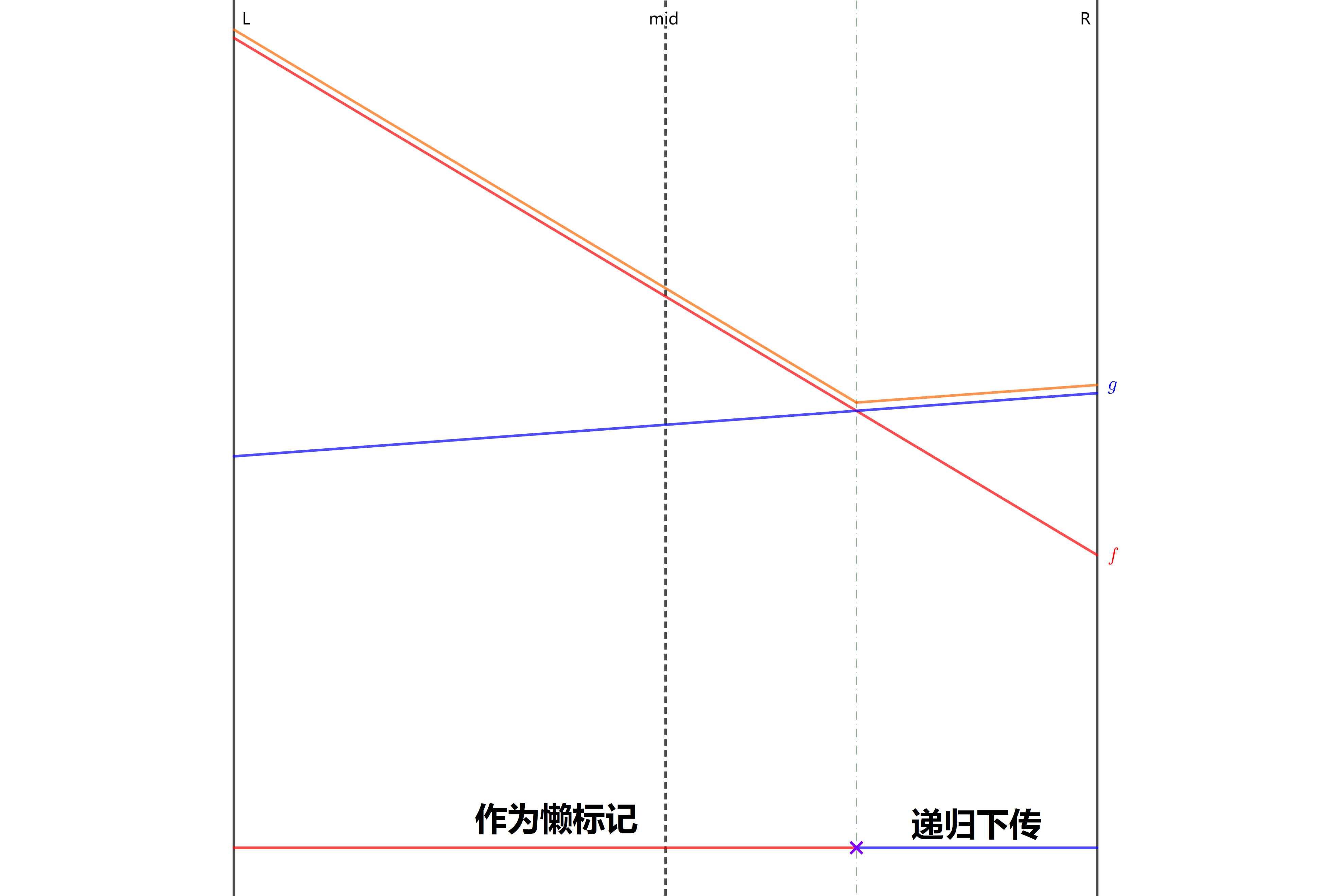
如图，按 \(f\) 取值是否大于 \(tg[x]\)，可以分出两个子区间。

• 一定有一个子区间超过一半，将 \(tg[x]\) 更新为这个子区间的答案。
• 对于另一个被左/右区间完全包含的子区间，可以直接递归下传标记。

显然这样做是不会漏掉任何线段的。

实现：

const double eps=1e-9;
inline int cmp(double x,double y){
    if(x-y>eps) return 1;
    if(y-x>eps) return -1;
    return 0;
}

//...

void updtg(int x,int l,int r,int id){
    if(!tg[x]) return tg[x]=id,void();
    int mid=(l+r)>>1;
    int fmid=cmp(calc(mid,id),calc(mid,tg[x]));
    if(fmid==1 || (!fmid && id<tg[x])) swap(id,tg[x]);
    int fl=cmp(calc(l,id),calc(l,tg[x])),fr=cmp(calc(r,id),calc(r,tg[x]));
    if(fl==1 || (!fl && id<tg[x])) updtg(ls[x],l,mid,id);
    if(fr==1 || (!fr && id<tg[x])) updtg(rs[x],mid+1,r,id);
}
void ins(int x,int l,int r,int s,int t,int id){
    if(l>=s && r<=t) return updtg(x,l,r,id);
    int mid=(l+r)>>1;
    if(s<=mid) ins(ls[x],l,mid,s,t,id);
    if(t>mid) ins(rs[x],mid+1,r,s,t,id);
}

查询

显然，根据标记的定义，所有包含 \(p\) 的子区间中，一定有一个是在 \(p\) 处取值最大的线段。

故可以直接递归比较得出答案。

实现：

Pdi que(int x,int l,int r,int p){
    Pdi res=(Pdi){calc(p,tg[x]),tg[x]};
    if(l==r) return res;
    int mid=(l+r)>>1;
    if(p<=mid) return pmax(res,que(ls[x],l,mid,p));
    return pmax(res,que(rs[x],mid+1,r,p));
}

---

时间复杂度

查询显然 \(O(\log n)\)

插入时，原线段拆分成 \(O(\log n)\) 个区间，每个区间需要 \(O(\log n)\) 时间递归下传，总复杂度 \(O(\log^2 n)\)

---

习题

CF660F Bear and Bowling 4

给定序列 \(\{a_n\}\) ，选取一个子序列 \([l,r]\) 使得 \(\sum\limits_{i=l}^{r} (i-l+1)\cdot a_{i}\) 最大。求这个最大值。

数据范围 \(n\le 2\times 10^5,|a_i|\le 10^7\)

记 \(s_i=\sum_{j=1}^i a_j,c_i=\sum_{j=1}^i j\cdot a_j\)

\(\begin{aligned} \sum\limits_{i=l}^{r} (i-l+1)\cdot a_{i} &=c_r-c_{l-1} - (s_r-s_{l-1})\cdot (l-1)\\ &=[s_{l-1}\cdot(l-1)-c_{l-1}]+[c_r-s_r\cdot(l-1)] \end{aligned}\)

对于同一个 \(l\)，左半部分是定值，右半部分是若干个一次函数。

显然我们可以用李超线段树来计算右半部分的最大值。