求最短路径的Dijkstra算法

 

目录

实验一：求最短路径的Dijkstra算法

目录：

一、 实验目的：

二、 实验内容：

三、 实验步骤：

（一） 设置头文件：

（二）编算法：

四、调试过程：

五、实验结果：

六、实验总结：

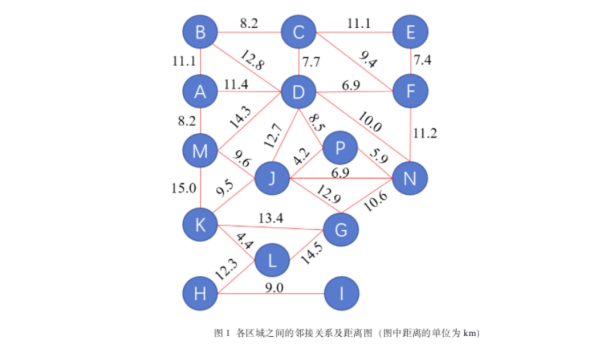
一、 实验目的：

解决求单源最短路径的问题。

题目：要求该地区各年各类事件密度在空间上的相关性，并给出不同区域相关性 最强的事件类别。求解相关性问题，即判断各个事件的事件密度和区域的关系。为 了计算的简便，我们将模型简化。需要利用 Dijkstra 算法求出到剩下 14 个区域有最短路径的区域，记该区域为中心区域。

 

二、 实验内容：

1. 在D盘建立文件夹“数据结构“，存放程序。
2. 启动Visual C++ 6.0,进入C编译集成环境。
3. 模型的准备 （1）广度优先搜索算法 Dijkstra 算法属于广度优先搜索算法。对比深度优先搜索算法，可以看出，广度 优先搜索算法在搜索所有答案的时候会采用由近及远的方式来搜索。先访问离起始 点最近的点，再访问远一些的点。换句话说，广度优先搜索会优先访问一步可以直 接到达的点，再访问走两步、三步或更多步可以到达的点。
4. 输入并运行Dijkstra求最短路径的程序。
5. 用Exel表格统计结果。

三、 实验步骤：

（一） 设置头文件：

#include <stdio.h>

#include <stdlib.h>

#include <malloc.h>

#include <string.h>

 

（二）编算法：

1、基础邻接表算法

#define MAX 100

#define INF (~(0x1<<31)) // 最大值

#define isLetter(a) ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))

#define LENGTH(a) (sizeof(a)/sizeof(a[0]))

// 邻接表中表对应的链表的顶点

typedef struct _ENode

{

 int ivex; // 该边的顶点的位置

 double weight; // 该边的权

 struct _ENode *next_edge; // 指向下一条弧的指针

}ENode, *PENode;

// 邻接表中表的顶点

typedef struct _VNode

{

 char data; // 顶点信息

 ENode *first_edge; // 指向第一条依附该顶点的弧

}VNode;

// 邻接表

typedef struct _LGraph

{

 int vexnum; // 图的顶点的数目

 int edgnum; // 图的边的数目

 VNode vexs[MAX];

}LGraph;

/*

* 返回 ch 在 matrix 矩阵中的位置

*/

static int get_position(LGraph G, char ch)

{

 int i;

 for(i=0; i<G.vexnum; i++)

 if(G.vexs[i].data==ch)

 return i;

 return -1;

}

/*42

* 读取一个输入字符

*/

static char read_char()

{

 char ch;

 do {

 ch = getchar();

 } while(!isLetter(ch));

 return ch;

}

/*

* 将 node 链接到 list 的末尾

*/

static void link_last(ENode *list, ENode *node)

{

 ENode *p;// = list;

p = list;

 while(p->next_edge)

 p = p->next_edge;

 p->next_edge = node;

}

/*

* 创建邻接表对应的图(自己输入)

*/

LGraph* create_lgraph()

{

 char c1, c2;

 int v, e;

 int i, p1, p2;

 int weight;

 ENode *node1=NULL, *node2=NULL;

 LGraph* pG=NULL;

 //"顶点数 v"和"边数 e"

v=15;

e=27;

 if ( v < 1 || e < 1 || (e > (v * (v-1))))

 {

 printf("input error: invalid parameters!\n");

 return NULL;

 }

 if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )

 return NULL;

 memset(pG, 0, sizeof(LGraph));

 // 初始化"顶点数"和"边数"

 pG->vexnum = v;

 pG->edgnum = e;

 // 初始化"邻接表"的顶点

 for(i=0; i<pG->vexnum; i++)

 {

 printf("vertex(%d): ", i);

 pG->vexs[i].data = read_char();

 pG->vexs[i].first_edge;

 }

 // 初始化"邻接表"的边

 for(i=0; i<pG->edgnum; i++)

 {

 // 读取边的起始顶点,结束顶点,权

 printf("edge(%d): ", i);

 c1 = read_char();

 c2 = read_char();

 scanf("%d", &weight);

 p1 = get_position(*pG, c1);

 p2 = get_position(*pG, c2);

 // 初始化 node1

 node1 = (ENode*)malloc(sizeof(ENode));

 node1->ivex = p2;

 node1->weight = weight;

 // 将 node1 链接到"p1 所在链表的末尾"

 if(pG->vexs[p1].first_edge == NULL)

 pG->vexs[p1].first_edge = node1;

 else

 link_last(pG->vexs[p1].first_edge, node1);

 // 初始化 node2

 node2 = (ENode*)malloc(sizeof(ENode));

 node2->ivex = p1;

 node2->weight = weight;

 // 将 node2 链接到"p2 所在链表的末尾"

 if(pG->vexs[p2].first_edge == NULL)

 pG->vexs[p2].first_edge = node2;

 else

 link_last(pG->vexs[p2].first_edge, node2);

 }

 return pG;

}

// 边的结构体

typedef struct _edata

{

 char start; // 边的起点

 char end; // 边的终点

 double weight; // 边的权重

}EData;

// 顶点

static char gVexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K','L','M','N','P'};

// 边

static EData gEdges[] = {

 // 起点 终点 权

 {'A', 'B', 11.1},

{'A', 'D', 11.4},

{'A', 'M', 8.2},

 {'B', 'C', 8.2},

{'B', 'D', 12.8},

 {'C', 'D', 7.7},

{'C', 'E', 11.1},

{'C', 'F', 9.4},

 {'D', 'F', 6.9},

{'D', 'P', 8.5},

{'D', 'J', 12.7},

{'D', 'N', 10},

{'D', 'M', 14.3},

 {'E', 'F', 7.4},

 {'F', 'N', 11.2},

{'G', 'N', 10.6},

{'G', 'J', 12.9},

{'G', 'L', 14.5},

{'G', 'K', 13.4},

{'H', 'I', 9.0},

{'H', 'L', 12.3},

{'J', 'P', 4.2},

{'J', 'M', 9.6},

{'J', 'K', 9.5},

{'K', 'L', 4.4},

{'K', 'M', 15.0},

{'N', 'P', 5.9},

};

/*

* 创建邻接表对应的图(用已提供的数据)

*/

LGraph* create_example_lgraph()

{

 char c1, c2;

 int vlen = LENGTH(gVexs);

 int elen = LENGTH(gEdges);

 int i, p1, p2;

 double weight;

 ENode *node1=NULL, *node2=NULL;//

 LGraph* pG=NULL;//

 if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )

 return NULL;

 memset(pG, 0, sizeof(LGraph));

 // 初始化"顶点数"和"边数"

 pG->vexnum = vlen;

 pG->edgnum = elen;

 // 初始化"邻接表"的顶点

 for(i=0; i<pG->vexnum; i++)

 {

 pG->vexs[i].data = gVexs[i];

 pG->vexs[i].first_edge = NULL;

 }

 // 初始化"邻接表"的边

 for(i=0; i<pG->edgnum; i++)

 {

 // 读取边的起始顶点,结束顶点,权

 c1 = gEdges[i].start;

 c2 = gEdges[i].end;

 weight = gEdges[i].weight;

 p1 = get_position(*pG, c1);

 p2 = get_position(*pG, c2);

 // 初始化 node1

 node1 = (ENode*)malloc(sizeof(ENode));

node1->next_edge=NULL;

 node1->ivex = p2;

 node1->weight = weight;

 // 将 node1 链接到"p1 所在链表的末尾"

 if(pG->vexs[p1].first_edge == NULL)

 pG->vexs[p1].first_edge = node1;

 else

 link_last(pG->vexs[p1].first_edge, node1);

 // 初始化 node2

 node2 = (ENode*)malloc(sizeof(ENode));

memset(node2, 0, sizeof(ENode));//renwx1

 node2->ivex = p1;

 node2->weight = weight;

 // 将 node2 链接到"p2 所在链表的末尾"

 if(pG->vexs[p2].first_edge == NULL)

 pG->vexs[p2].first_edge = node2;

 else

 link_last(pG->vexs[p2].first_edge, node2);

 }

 return pG;

}

/*

* 深度优先搜索遍历图的递归实现

*/

static void DFS(LGraph G, int i, int *visited)

{

 ENode *node;

 visited[i] = 1;

 printf("%c ", G.vexs[i].data);

 node = G.vexs[i].first_edge;

 while (node != NULL)

 {

 if (!visited[node->ivex])

 DFS(G, node->ivex, visited);

 node = node->next_edge;

 }

}

/*

* 深度优先搜索遍历图

*/

void DFSTraverse(LGraph G)

{

 int i;

 int visited[MAX]; // 顶点访问标记

 // 初始化所有顶点都没有被访问

 for (i = 0; i < G.vexnum; i++)

 visited[i] = 0;

 printf("DFS: ");

 for (i = 0; i < G.vexnum; i++)

 {

 if (!visited[i])

 DFS(G, i, visited);

 }

 printf("\n");

}

/*

* 广度优先搜索（类似于树的层次遍历）

*/

void BFS(LGraph G)

{

 int head = 0;

 int rear = 0;

 int queue[MAX]; // 辅组队列

 int visited[MAX]; // 顶点访问标记

 int i, j, k;

 ENode *node=NULL; //初始化指针

 for (i = 0; i < G.vexnum; i++)

 visited[i] = 0;

 printf("BFS: ");

 for (i = 0; i < G.vexnum; i++)

 {

 if (!visited[i])

 {

 visited[i] = 1;

 printf("%c ", G.vexs[i].data);

 queue[rear++] = i; // 入队列

 }

 while (head != rear)

 {

 j = queue[head++]; // 出队列

 node = G.vexs[j].first_edge;

 while (node != NULL)

 {

 k = node->ivex;

 if (!visited[k])

 {

 visited[k] = 1;

 printf("%c ", G.vexs[k].data);

 queue[rear++] = k;

 }

 node = node->next_edge;

 }

 }

 }

 printf("\n");

}

/*

* 打印邻接表图

*/

void print_lgraph(LGraph G)

{

 int i;

 ENode *node;

 printf("List Graph:\n");

 for (i = 0; i < G.vexnum; i++)

 {

 printf("%d(%c): ", i, G.vexs[i].data);

 node = G.vexs[i].first_edge;

 while (node != NULL)

 {

 printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data);

 node = node->next_edge;

 }

 printf("\n");

 }

}

double get_weight(LGraph G, int start, int end)

{

 ENode *node;

 if (start==end)

 return 0;

 node = G.vexs[start].first_edge;

 while (node!=NULL)

 {

 if (end==node->ivex)

 return node->weight;

 node = node->next_edge;

 }

 return INF;

}

/*

* 获取图中的边

*/

EData* get_edges(LGraph G)

{

 int i;//,j;

 int index=0;

 ENode *node;

 EData *edges;

 edges = (EData*)malloc(G.edgnum*sizeof(EData));

 for (i=0; i<G.vexnum; i++)

 {

 node = G.vexs[i].first_edge;

 while (node != NULL)

 {

 if (node->ivex > i)

 {

 edges[index].start = G.vexs[i].data; // 起点

 edges[index].end = G.vexs[node->ivex].data; // 终点

 edges[index].weight = node->weight; // 权

 index++;

 }

 node = node->next_edge;

 }

 }

 return edges;

}

/*

* 对边按照权值大小进行排序(由小到大)

*/

void sorted_edges(EData* edges, int elen)

{

 int i,j;

 for (i=0; i<elen; i++)

 {

 for (j=i+1; j<elen; j++)

 {

 if (edges[i].weight > edges[j].weight)

 {

 // 交换"第 i 条边"和"第 j 条边"

 EData tmp = edges[i];

 edges[i] = edges[j];

 edges[j] = tmp;

 }

 }

 }

}

/*

* 获取 i 的终点

*/

int get_end(int vends[], int i)

{

 while (vends[i] != 0)

 i = vends[i];

 return i;

}

2.设计Dijkstra子函数

/*

* Dijkstra 最短路径。

* 即，统计图(G)中"顶点 vs"到其它各个顶点的最短路径。51

*

* 参数说明：

* G -- 图

* vs -- 起始顶点(start vertex)。即计算"顶点 vs"到其它顶点的最短路径。

* prev -- 前驱顶点数组。即，prev[i]的值是"顶点 vs"到"顶点 i"的最短路径所经历的全部顶点中，位于"顶点 i"之前的那个顶点。

* dist -- 长度数组。即，dist[i]是"顶点 vs"到"顶点 i"的最短路径的长度。

*/

void dijkstra(LGraph G, int vs, double prev[], double dist[])

{

 int i,j,k;

 double min,tmp;

 int flag[MAX]; // flag[i]=1 表示"顶点 vs"到"顶点 i"的最短路径已成功获取。

 // 初始化

 for (i = 0; i < G.vexnum; i++)

 {

 flag[i] = 0; // 顶点 i 的最短路径还没获取到。

 prev[i] = 0; // 顶点 i 的前驱顶点为 0。

 dist[i] = get_weight(G, vs, i); // 顶点 i 的最短路径为"顶点 vs"到"顶点 i"的权。

 }

 // 对"顶点 vs"自身进行初始化

 flag[vs] = 1;

 dist[vs] = 0;

 // 遍历 G.vexnum-1 次；每次找出一个顶点的最短路径。

 for (i = 1; i < G.vexnum; i++)

 {

 // 寻找当前最小的路径；

 // 即，在未获取最短路径的顶点中，找到离 vs 最近的顶点(k)。

 min = INF;

 for (j = 0; j < G.vexnum; j++)

 {

 if (flag[j]==0 && dist[j]<min)

 {

 min = dist[j];

 k = j;

 }

 }

 // 标记"顶点 k"为已经获取到最短路径

 flag[k] = 1;

 // 修正当前最短路径和前驱顶点

 // 即，当已经"顶点 k 的最短路径"之后，更新"未获取最短路径的顶点的最短路径和前驱顶点"。52

 for (j = 0; j < G.vexnum; j++)

 {

 tmp = get_weight(G, k, j);

 tmp = (tmp==INF ? INF : (min + tmp)); // 防止溢出

 if (flag[j] == 0 && (tmp < dist[j]) )

 {

 dist[j] = tmp;

 prev[j] = k;

 }

 }

 }

 // 打印 dijkstra 最短路径的结果

 printf("dijkstra(%c): \n", G.vexs[vs].data);

 for (i = 0; i < G.vexnum; i++)

 printf(" shortest(%c, %c)=%-3.1f\n", G.vexs[vs].data, G.vexs[i].data, dist[i]);

}

3、编主函数：

void main()

{

 double prev[MAX] = {0};

 double dist[MAX] = {0};

 LGraph* pG;

 // 采用已有的"图"

 pG = create_example_lgraph();

 BFS(*pG); // 广度优先遍历

 // dijkstra 算法获取"第 i+1 个顶点"到其它各个顶点的最短距离

for(int i=0;i<LENGTH(gVexs);++i)

dijkstra(*pG,i, prev, dist);

}

四、 调试过程：

1. 第一次编写程序时，讲权值设为int类型了，应改为double类型，编译才通过。
2. 程序里面已经定义了的数据，在主函数中选择直接使用自定义的图，命令为pG=create_lgraph();，而非用键盘输入。
3. 为调试方便，对顶点数和边数直接赋值。

五、实验结果：

根据 Dijkstra 算法可得如下表格：

 

表 4：有关求区域最短路径的数据

由表格可知，J 区域为我们要求的中心区域。

六、实验总结：

1、注意变量的数据类型。

2、注意，申请结点时，要初始化。因为代码里面，访问了未初始化的数据，访问完后清零，这是一个避免程序编译出错的好习惯。

3、初始化后就memset( )，清零。

4、对于不可预测的数据，在访问时，指针会崩溃，因为这属于访问了非法地址。若用非指针的变量去访问，则会报错。