第三章 数据探索

一、分布分析

对定量数据进行特征分析

 

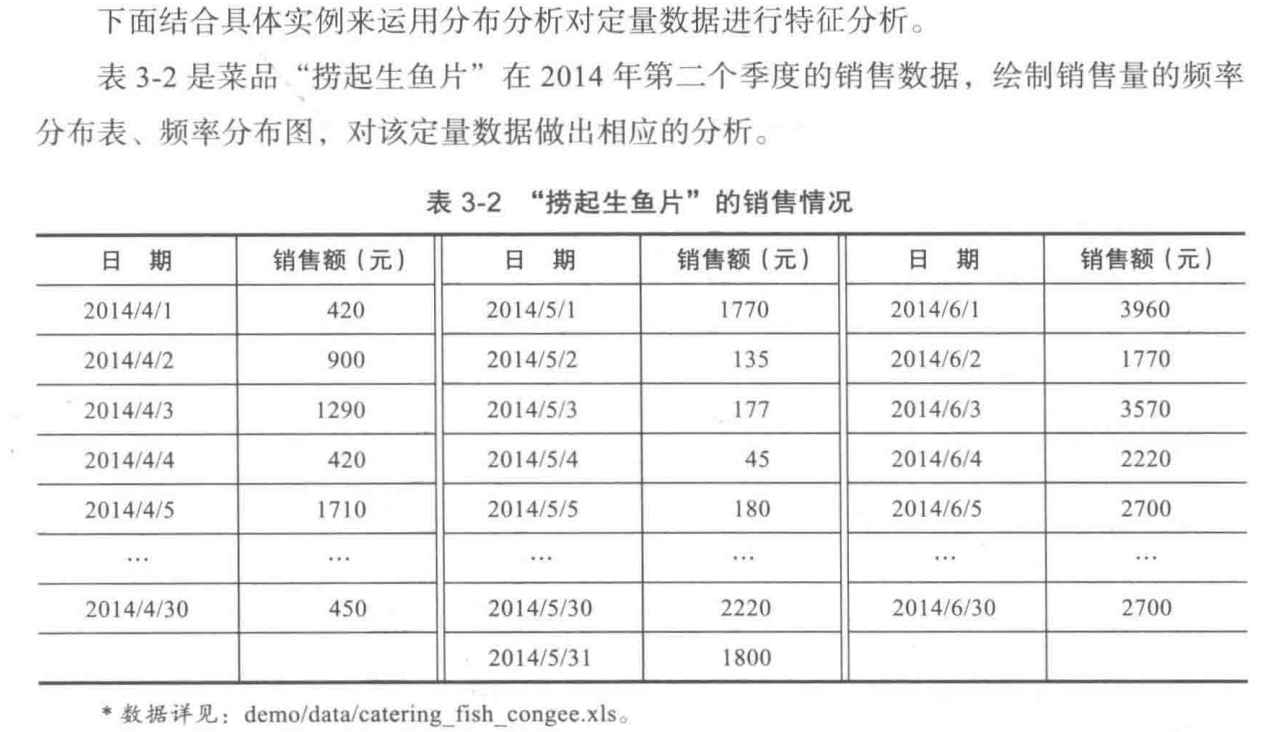
1、 观察数据

import pandas as pd
import numpy as np
catering_sale = '../大三下/catering_fish_congee1.xls'  # 餐饮数据
data = pd.read_excel(catering_sale,index_col=u'日期')  # 读取数据，指定“日期”列为索引
print(data.describe(),data.describe().max()-data.describe().min())

 

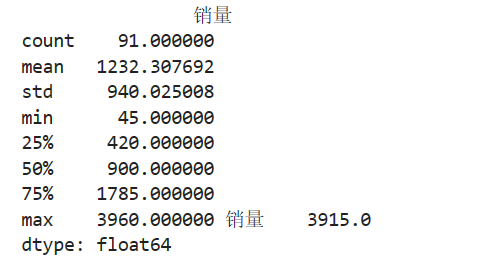
2、画图分析

2.1 箱型图

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.figure()
p = data.boxplot(return_type='dict')
x = p['fliers'][0].get_xdata()
y = p['fliers'][0].get_ydata()
plt.title('季度销售额箱型图_number 035',fontsize=20)
y.sort()

for i in range(len(x)):
    if i>0:
        plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.055 -0.8/(y[i]-y[i-1]),y[i]))
    else:
        plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.058,y[i]))

plt.show()  # 展示箱线图

 

 注意：

用annotate添加注释
其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制
本代码中的参数都是经过调试的，需要具体问题具体调试。

 　　比如下面的图：

import numpy as np
import matplotlib.pyplot as plt
 
# 以步长0.005绘制一个曲线
x = np.arange(0, 10, 0.005)
y = np.exp(-x/2.) * np.sin(2*np.pi*x)
 
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlim(0, 10)
ax.set_ylim(-1, 1)
 
# 被注释点的数据轴坐标和所在的像素
xdata, ydata = 5, 0
xdisplay, ydisplay = ax.transData.transform_point((xdata, ydata))
 
# 设置注释文本的样式和箭头的样式
bbox = dict(boxstyle="round", fc="0.8")
arrowprops = dict(
    arrowstyle = "->",
    connectionstyle = "angle,angleA=0,angleB=90,rad=10")
 
# 设置偏移量
offset = 72
# xycoords默认为'data'数据轴坐标，对坐标点（5,0）添加注释
# 注释文本参考被注释点设置偏移量，向左2*72points，向上72points
ax.annotate('data = (%.1f, %.1f)'%(xdata, ydata),
            (xdata, ydata), xytext=(-2*offset, offset), textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)
 
# xycoords以绘图区左下角为参考，单位为像素
# 注释文本参考被注释点设置偏移量，向右0.5*72points，向下72points
disp = ax.annotate('display = (%.1f, %.1f)'%(xdisplay, ydisplay),
            (xdisplay, ydisplay), xytext=(0.5*offset, -offset),
            xycoords='figure pixels',
            textcoords='offset points',
            bbox=bbox, arrowprops=arrowprops)
 
 
plt.show()

 

 

 2.2 画直方图

（1）分成8类

 

 

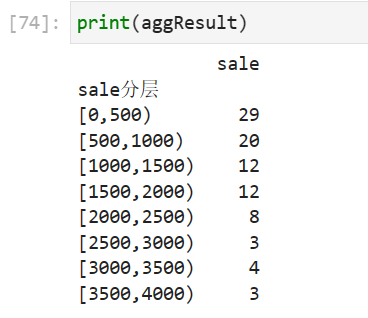
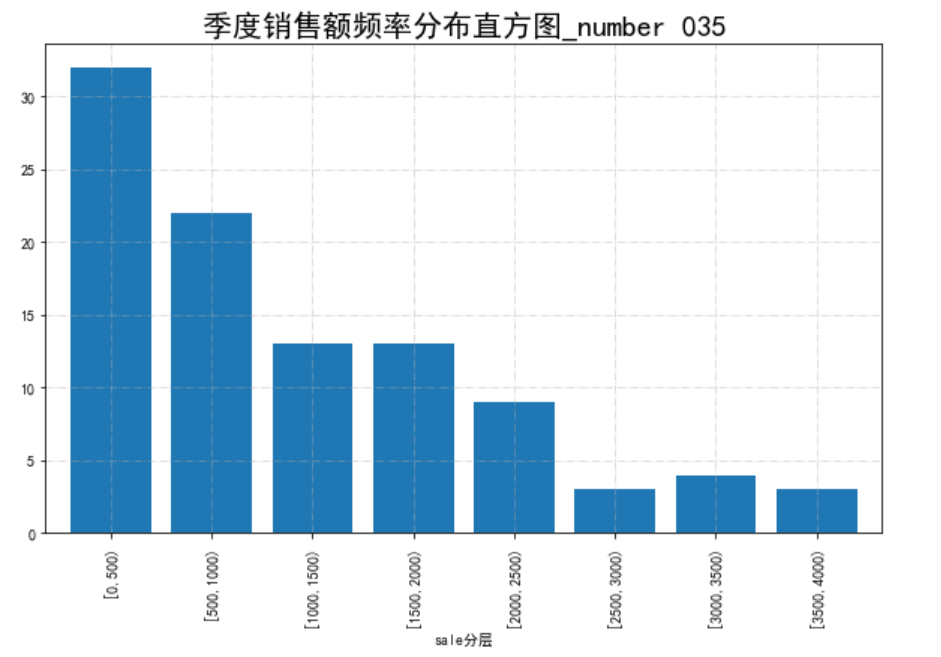
# 分成8类
data = pd.read_excel(catering_sale,names=['date','sale'])  # 读取数据，指定“日期”列为索引
bins = [0,500,1000,1500,2000,2500,3000,3500,4000]
labels = ['[0,500)','[500,1000)','[1000,1500)','[1500,2000)',
       '[2000,2500)','[2500,3000)','[3000,3500)','[3500,4000)'] 

data['sale分层'] = pd.cut(data.sale, bins, labels=labels) #cut分层
# aggResult = data.groupby(by=['sale分层'])['sale'].agg({'sale': np.size})
aggResult = data.groupby('sale分层').agg({'sale':'count'})

pAggResult = round(aggResult/aggResult.sum(), 2, ) * 100

import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))  # 设置图框大小尺寸
pAggResult['sale'].plot(kind='bar',width=0.8,fontsize=10)  # 绘制频率直方图
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.title('季度销售额频率分布直方图_number 035',fontsize=20)
plt.grid(alpha=0.5,linestyle='-.') #网格线，更好看 
plt.show()

 

（2）分成4类

# 分成4类
data = pd.read_excel(catering_sale,names=['date','sale'])  # 读取数据，指定“日期”列为索引
bins = [0,1000,2000,3000,4000]
labels = ['[0,1000)','[1000,2000)',
       '[2000,3000)','[3000,4000)'] 

data['sale分层'] = pd.cut(data.sale, bins, labels=labels) #cut分层
# aggResult = data.groupby(by=['sale分层'])['sale'].agg({'sale': np.size})
aggResult = data.groupby('sale分层').agg({'sale':'count'})
print(aggResult)
pAggResult = round(aggResult/aggResult.sum(), 2, ) * 100

import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))  # 设置图框大小尺寸
pAggResult['sale'].plot(kind='bar',width=0.8,fontsize=10)  # 绘制频率直方图
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.title('季度销售额频率分布直方图_number 035',fontsize=20)
plt.grid(alpha=0.5,linestyle='-.') #网格线，更好看 
plt.show()

 python知识：运用cut函数和groupby函数对数据进行分组

 

对定性数据进行特征分析

对于定性变量，常常根据变量的分类类型来分组，可以采用饼图和条形图来描述定性变量的分布。

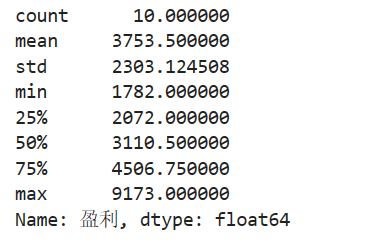
import pandas as pd
import matplotlib.pyplot as plt
catering_dish_profit = '../大三下/catering_dish_profit.xls'
data = pd.read_excel(catering_dish_profit)
print(data['盈利'].describe())

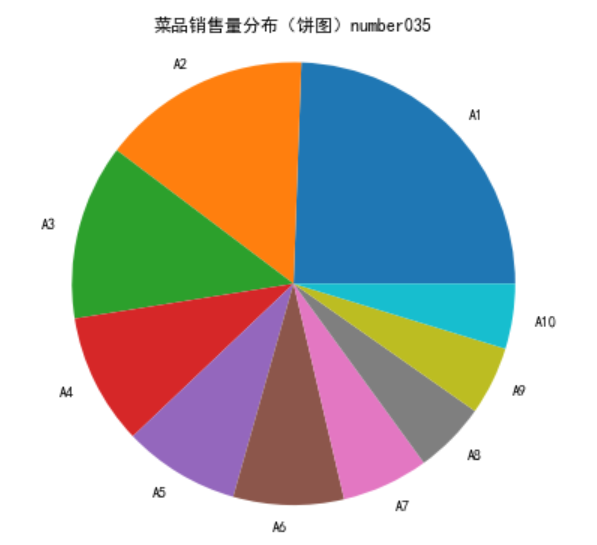
# 绘制饼图
x = data['盈利']
labels = data['菜品名']
plt.figure(figsize = (8,6))  #设置画布大小
plt.pie(x,labels=['A1','A2','A3','A4','A5','A6','A7','A8','A9','A10']) # 设置饼图标签)  #绘制饼图
plt.rcParams['font.sans-serif']='SimHei'
plt.title('菜品销售量分布（饼图）number035')   #设置标题
plt.axis('equal')
plt.show()

由图可得不同菜品在某段时间的销售量分布图

饼图的每一个扇形部分代表每一类型的所占百分比或频数，根据定性变量的类型数目将饼图分成几个部分，每一部分的大小与每一类型的频数成正比;

条形图的高度代表每一类型的百分比或频数，而条形图的宽度没有意义。

二、对比分析

对比分析是指把两个相互联系的指标进行比较，从数量上展示和说明研究对象规模的大小、水平的高低、速度的快慢以及各种关系是否协调。特别适用于指标间的横纵向比较、时间序列的比较分析。

在对比分析中，选择合适的对比标准是十分关键的，选得合适才能做出客观评价；选得不合适，评价后可能得出错误的结论。
对比分析主要有以下两种形式：

2.1 绝对数比较

2.2 相对数比较

 

 

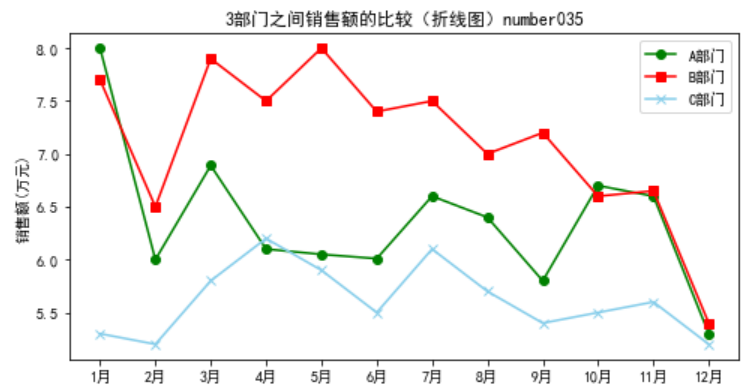
以各菜品的销售数据为例，从时间维度上分析，可以看到A部门、B部门、C部门3个部门的销售金额随时间的变化趋势，可以了解在此期间哪个部门的销售金额较高，趋势比较平稳，也可以从单一部门(B 部门)做分析，了解各年份的销售对比情况。

运行代码可得3个部门的销售金额随时间的变化趋势，以及B部门在不同年份的销售额随时间的变化趋势，如下两图所示

#部门之间销售金额比较
import pandas as pd
import matplotlib.pyplot as plt
data=pd.read_excel("../大三下/dish_sale.xls")
plt.figure(figsize=(8,4))
plt.plot(data['月份'],data['A部门'],color='green',label='A部门',marker='o')
plt.plot(data['月份'],data['B部门'],color='red',label='B部门',marker='s')
plt.plot(data['月份' ],data['C部门'],color='skyblue',label='C部门', marker='x')
plt.legend()#显示图例
plt.rcParams['font.sans-serif']='SimHei'
plt.title('3部门之间销售额的比较（折线图）number035')   #设置标题
plt.ylabel('销售额(万元)')
plt.show()

 

 

#B部门各年份之间销售金额的比较
data=pd.read_excel("../大三下/dish_sale_b.xls")
plt.figure(figsize=(8,4))
plt.plot(data['月份'],data['2012年'],color='green',label='2012年',marker='o')
plt.plot(data['月份'],data['2013年'],color='red',label='2013年',marker='s')
plt.plot(data['月份' ],data['2014年'],color='skyblue',label='2014年', marker='x')
plt.rcParams['font.sans-serif']='SimHei'
plt.title('B部门各年份销售额的比较（折线图）number035')   #设置标题
plt.legend() #显示图例
plt.ylabel('销售额(万元)')
plt.show()

 

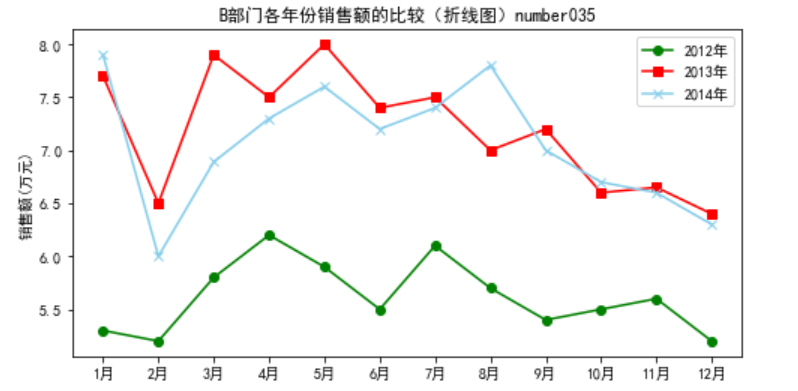
 总体来看，3个部门的销售额呈递减趋势;A部门和C部门的递减趋势比较平稳;B部门的销售额下降趋势比较明显，进一步分析造成这种现象的原因，可能是原材料不足。

 

三、统计量分析

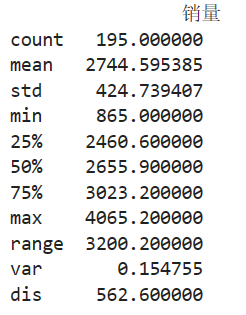
　　用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。平均水平指标是对个体集中趋势的度量，使用最广泛的是均值和中位数:反映变异程度的指标则是对个体离开平均水平的度量，使用较广泛的是标准差(方差)、四分位间距。

# 餐饮销量数据统计量分析
import pandas as pd

catering_sale = '../大三下/catering_sale.xls'  # 餐饮数据
data = pd.read_excel(catering_sale, index_col = '日期')  # 读取数据，指定“日期”列为索引列
data = data[(data['销量'] > 400)&(data['销量'] < 5000)]  # 过滤异常数据
statistics = data.describe()  # 保存基本统计量

statistics.loc['range'] = statistics.loc['max']-statistics.loc['min']  # 极差
statistics.loc['var'] = statistics.loc['std']/statistics.loc['mean']  # 变异系数
statistics.loc['dis'] = statistics.loc['75%']-statistics.loc['25%']  # 四分位数间距

print(statistics)

 

 

四、周期性分析

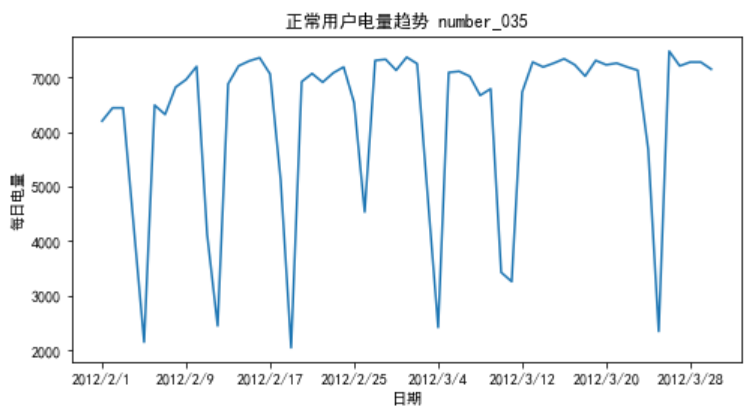
　　周期性分析是探索某个变量是否随着时间的变化而呈现出某种周期变化趋势。时间尺度相对较长的周期性趋势有年度周期性趋势、季节性周期性趋势;时间尺度相对较短的有月度周期性趋势、周度周期性趋势，甚至更短的天、小时周期性趋势。

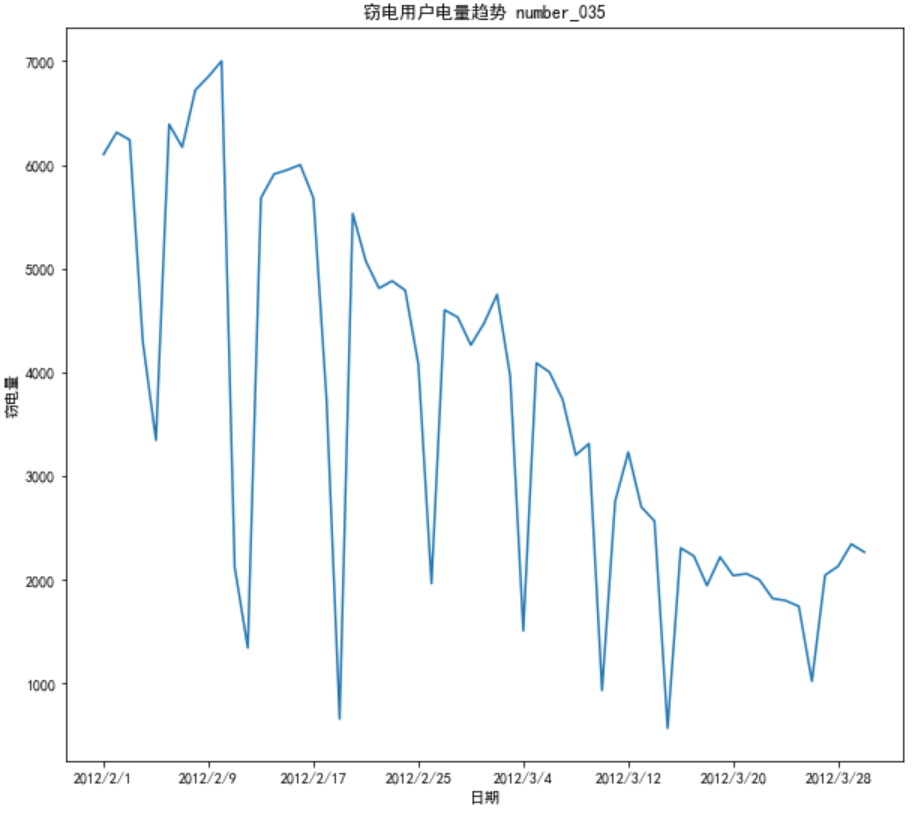
　　例如，要对正常用户和窃电用户在2012年2月份与3月份日用电量进行预测，可以分别分析正常用户和窃电用户的日用电量的时序图，来直观地估计其用电量变化趋势如下代码所示。

# 某单位日用电量预测分析

import pandas as pd
import matplotlib.pyplot as plt

df_normal = pd.read_csv("../大三下/user.csv")
plt.figure(figsize=(8,4))
plt.plot(df_normal["Date"],df_normal["Eletricity"])
plt.xlabel("日期")
plt.ylabel("每日电量")
# 设置x轴刻度间隔
x_major_locator = plt.MultipleLocator(8)
ax = plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
plt.title("正常用户电量趋势 number_035")
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.show()  # 展示图片

 

 

 

# 窃电用户用电趋势分析
df_steal = pd.read_csv("../大三下/Steal user.csv")
plt.figure(figsize=(10, 9))
plt.plot(df_steal["Date"],df_steal["Eletricity"])
plt.xlabel("日期")
plt.ylabel("窃电量)
# 设置x轴刻度间隔
x_major_locator = plt.MultipleLocator(8)
ax = plt.gca()
ax.xaxis.set_major_locator(x_major_locator)
plt.title("窃电用户电量趋势 number_035")
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.show()  # 展示图片

五、贡献度分析

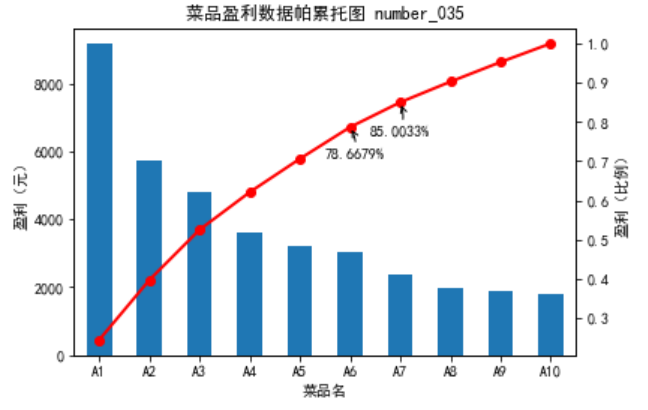
　　贡献度分析又称帕累托分析，它的原理是帕累托法则，又称 20/80 定律。同样的投人放在不同的地方会产生不同的效益。例如，对一个公司来讲，80% 的利润常常来自于20%最畅销的产品，而其他80%的产品只产生了20%的利润。　　

　　盈利帕累托图（二八原则）

 

 

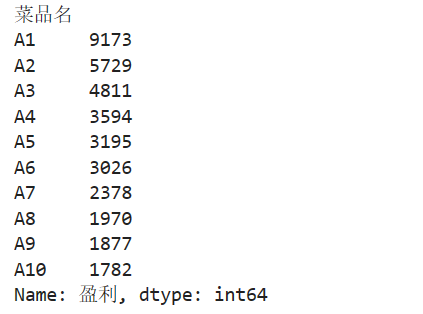
 step1 处理菜品盈利数据

# 菜品盈利帕累托图

# 菜品盈利数据 帕累托图
import pandas as pd

# 初始化参数
dish_profit = '../大三下/catering_dish_profit.xls'  # 餐饮菜品盈利数据
data = pd.read_excel(dish_profit, index_col = '菜品名')
data = data['盈利'].copy()
data.sort_values(ascending = False)
print(data)

 

 step2 作帕累托图

import matplotlib.pyplot as plt  # 导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

plt.figure()
data.plot(kind='bar')
plt.ylabel('盈利（元）')
p = 1.0*data.cumsum()/data.sum()
p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))  # 添加注释，即85%处的标记。这里包括了指定箭头样式。
plt.annotate(format(p[5], '.4%'), xy = (5, p[5]), xytext=(5*0.9, p[5]*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))  # 添加注释，即78%处的标记。这里包括了指定箭头样式。

plt.title("菜品盈利数据帕累托图 number_035")
plt.ylabel('盈利（比例）')
plt.show()

 

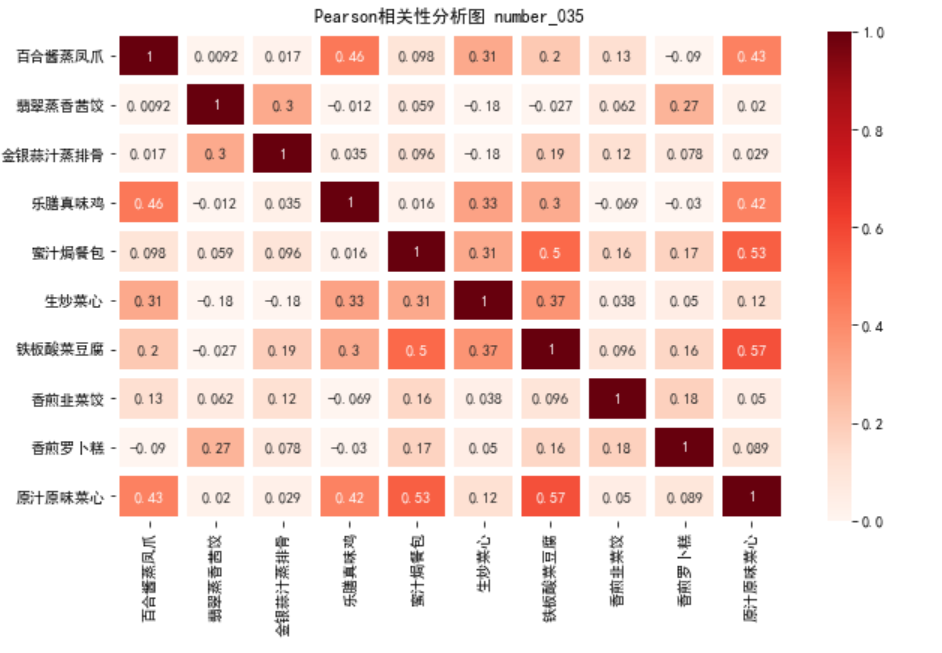
六、相关性分析

# 餐饮销量数据相关性分析
from __future__ import print_function
import pandas as pd

catering_sale = '../大三下/catering_sale_all.xls'  # 餐饮数据，含有其他属性
data = pd.read_excel(catering_sale, index_col = '日期')  # 读取数据，指定“日期”列为索引列

print(data.corr())  # 相关系数矩阵，即给出了任意两款菜式之间的相关系数
print(data.corr()['百合酱蒸凤爪'])  # 只显示“百合酱蒸凤爪”与其他菜式的相关系数
# 计算“百合酱蒸凤爪”与“翡翠蒸香茜饺”的相关系数
print(data['百合酱蒸凤爪'].corr(data['翡翠蒸香茜饺']))

 

Pearson相关系数

提供了对于变量取值范围不同的处理步骤

import pandas  as pd
import numpy   as np
import matplotlib.pyplot as plt
import seaborn as sns

# 1.数据
df = pd.DataFrame(data)
print(df)

# 2.相关分析热力图可视化, df.corr()默认参数为pearson

plt.figure(figsize=[10, 6])
plt.title("Pearson相关性分析图 number_035")
sns.heatmap(df.corr(), vmin=0, vmax=1, cmap="Reds", linewidths=5.5, annot=True)
plt.show()

 

Spearman等级相关系数

遇到定类变量或者定序变量的“相关系数”，就需要用到Spearman（斯皮尔曼）等级相关系数和Kendall（肯德尔）的tau相关系数。

# 相关分析热力图可视化, df.corr() method=spearman指定系数
plt.figure(figsize=[10, 6])
plt.title("Spearman相关性分析热力图 number_035")
sns.heatmap(df.corr(method='spearman'), vmin=0, vmax=1, cmap="Reds", linewidths=0.5, annot=True)
plt.show()

 

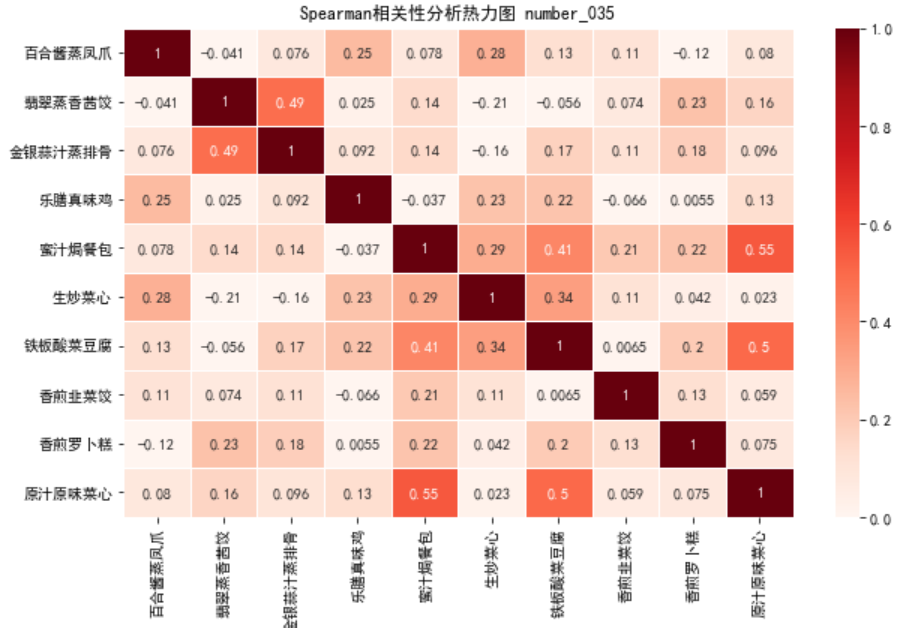
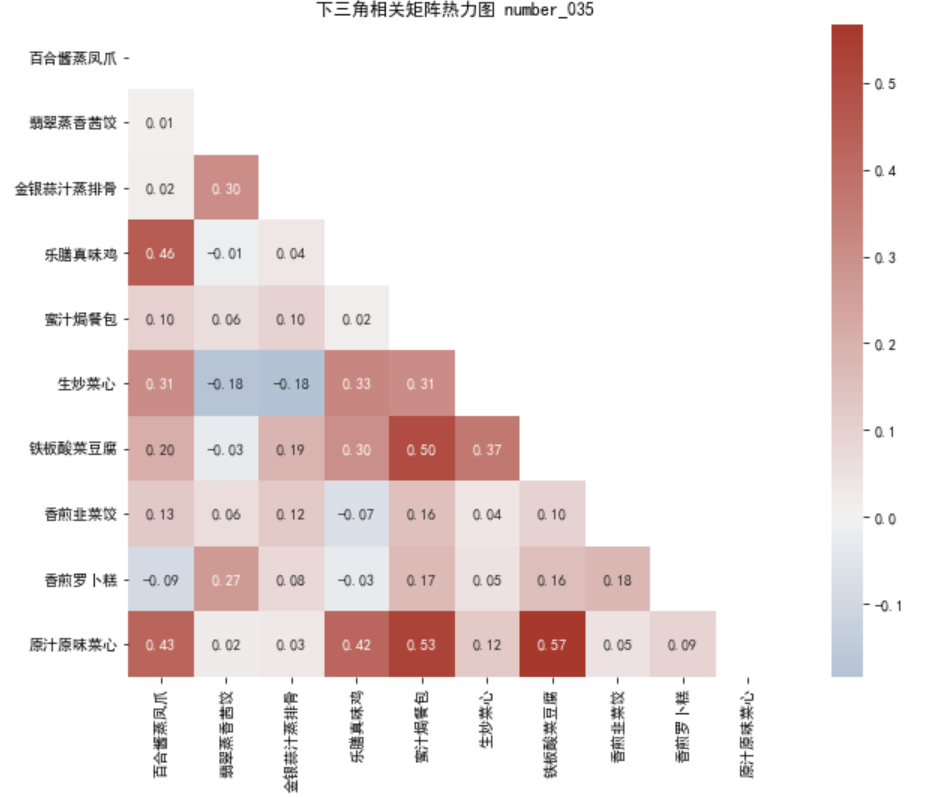
下三角相关性矩阵

 相关性矩阵绘制的是两两变量之间的相关性，所以是一个对称的矩阵，所以只需保留上三角矩阵或者下三角矩阵的内容即可。

# 下三角相关矩阵热力图
plt.figure(figsize=[10, 6])
matrix = df.corr()
cmap = sns.diverging_palette(250, 15, s=75, l=40, n=9, center="light", as_cmap=True)
# mask掉上三角部分
mask = np.triu(np.ones_like(matrix, dtype=bool))
plt.figure(figsize=(12, 8))
plt.title("下三角相关矩阵热力图 number_035")
sns.heatmap(matrix,  mask=mask, center=0, annot=True, fmt='.2f', square=True, cmap=cmap) 
plt.show()

 

 参考链接：https://blog.csdn.net/SeafyLiang/article/details/120256956

 

 

补充作图：

def draw_correct_line():
 import math
 import numpy as np
 import matplotlib.pyplot as plt
 import pylab
 x=np.arange(0,2*np.pi,0.01)
 x=x.reshape(len(x),1)
 y=np.sin(x)
 pylab.plot(x,y,label='sin')
 plt.axhline(linewidth=1,color='r')
 plt.show()
plt.rcParams['font.sans-serif']='SimHei'
plt.title('y=sin(x) by number035')   #设置标题
draw_correct_line()