从《好消息，坏消息》（洛谷P2629）谈单调队列

单调队列是指：队列中元素之间的关系具有单调性，而且，队首和队尾都可以进行出队操作，只有队尾可以进行入队操作。

队列是一种先进先出(FIFO First In First Out)的数据结构，它类似于下面这幅图：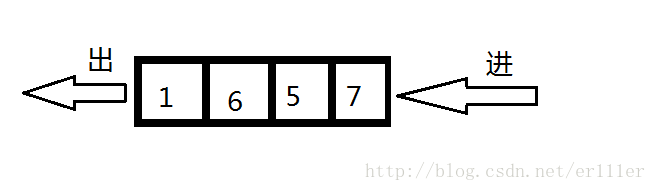

 

优先队列应该是一种维护区间最大最小值的优化算法，时间复杂度为O（n）

以查找最大值为例：

假设使用head和tail代表队列的头和尾部

对于每一个新加入的值v：

如果v的值比tail大，则tail的值对于之前的区间一定不是最大值（只有一个元素除外），对于后面的区间又没有v的值有用，

本着去除杂的中心思想，tail可以被弹出，并压入v。

同时，按照上述方式入队，可以保证队列的单调性，队首head则代表了当前区间的最大值。

以下是从大佬借鉴的代码：

int q[maxn];

int head=1,tail=0;

while(head<=tail&&q[tail]<v[i])--tail;

q[++tail]=i;//记录下坐标

while(check())++head;//维护左边区间

 

下面是例题：

题目描述

uim在公司里面当秘书，现在有n条消息要告知老板。每条消息有一个好坏度，这会影响老板的心情。告知完一条消息后，老板的心情等于之前老板的心情加上这条消息的好坏度。最开始老板的心情是0，一旦老板心情到了0以下就会勃然大怒，炒了uim的鱿鱼。

uim为了不被炒，知道了了这些消息（已经按时间的发生顺序进行了排列）的好坏度，希望研究如何不让老板发怒。

uim必须按照时间的发生顺序逐条将消息告知给老板。不过uim可以使用一种叫“倒叙”的手法，例如有n条消息，小a可以从k,k+1,k+2...n,1,2...k-1这种顺序通报。

他希望知道，有多少个k，从k开始通报到n然后从1通报到k-1可以让老板不发怒。

输入格式

第一行一个整数n(1 <= n <= 10^6)，表示有n个消息。

第二行n个整数，按时间顺序给出第i条消息的好坏度Ai(-1000 <= Ai <= 1000)

输出格式

一行一个整数，表示可行的方案个数。

输入输出样例

输入 #1复制

4
-3 5 1 2 

输出 #1复制

2

说明/提示

样例解释

[5 1 2 -3]或[1 2 -3 5]

对于25%数据n<=1000

对于75%数据n<=10000

对于100%数据n<=10^6

 

对于循环链表，我们可以使用断环成链的方式，使用双倍大小的数组。

于是题目就变成了，判断区间【i,j】中任意从【i,k】(i<=k<=j)是否之和大于0，如果小于0，则不能从这里开始讲述。

于是我们可以采用 前缀和+优先队列 的思想，优先队列用于判断这段区间中最小的s[k],只要最小的s[k]-s[i-1]>0,则全都大于0；

以下是代码：

#include<iostream>
using namespace std;
const int maxn=1e6+1;

int message[2*maxn],pre[2*maxn],id[maxn];
int main(){
    
    int n,l=1,r=0;
    scanf("%d",&n);
    pre[0]=0;
    for(register int i=1;i<=n;++i){
        scanf("%d",&message[i]);
        pre[i]=pre[i-1]+message[i];
        while(l<=r&&pre[id[r]]>pre[i])--r;
        id[++r]=i;
    }
    for(register int i=n+1;i<2*n;++i){
        message[i]=message[i-n];
        pre[i]=pre[i-1]+message[i];
    }
    int bad=0;
    for(register int i=1;i<=n;++i){
        if(pre[id[l]]-pre[i-1]<0)++bad;
        while(l<=r&&pre[id[r]]>pre[i+n])--r;
        id[++r]=i+n;
        if(pre[i]==pre[id[l]])++l;
    }
    printf("%d",n-bad);
    return 0;
}

总结：

1、优先队列可以用来快速查找一段区间的最大最小值。

2、任意区间的所有满足某一条件 考虑最大最小值满足该条件。

3、断环成链 前缀和思想。