圆中的几个基本定理

Ptolomy 定理

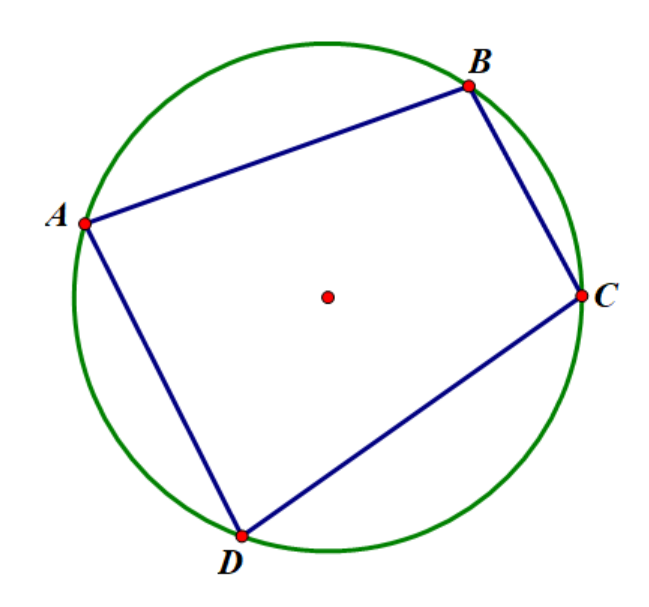
圆内接四边形 \(ABCD\) 满足条件：

\[AB\cdot CD+AD\cdot BC=BD\cdot AC \]

证明：一条对角线拆开构造两个相似即得。

其逆定理也成立。

Simson 定理

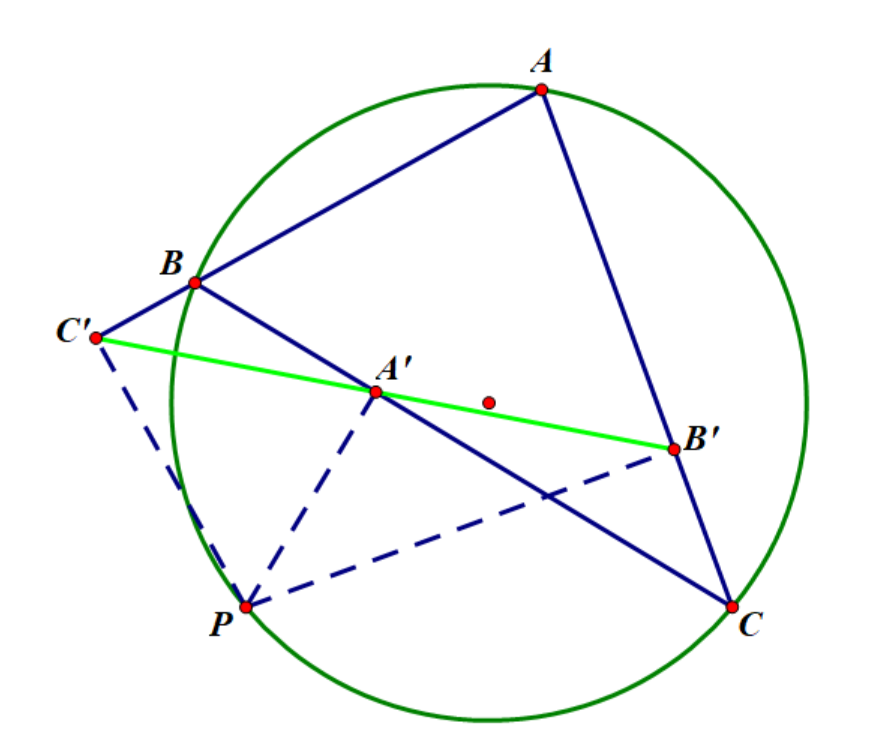
过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线，则三垂足共线（Simson 线）。

证明： \(\angle PA'C'=\angle PBC',\angle PA'B'=180^\circ-\angle PCA=\angle PBA\)，

所以 ，即得共线。

圆幂定理

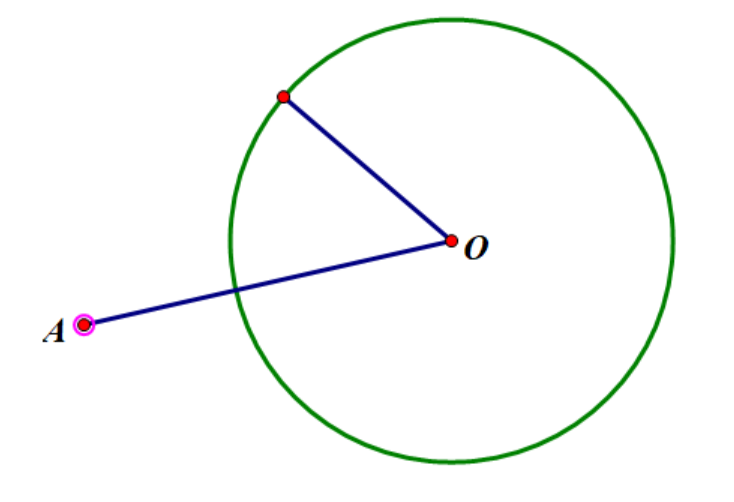
\(A\) 到 \(\odot O\) 的幂 \(M=d^2-r^2\) ，有相交弦定理，切割线定理，割线定理。

Monge 定理（根心定理）

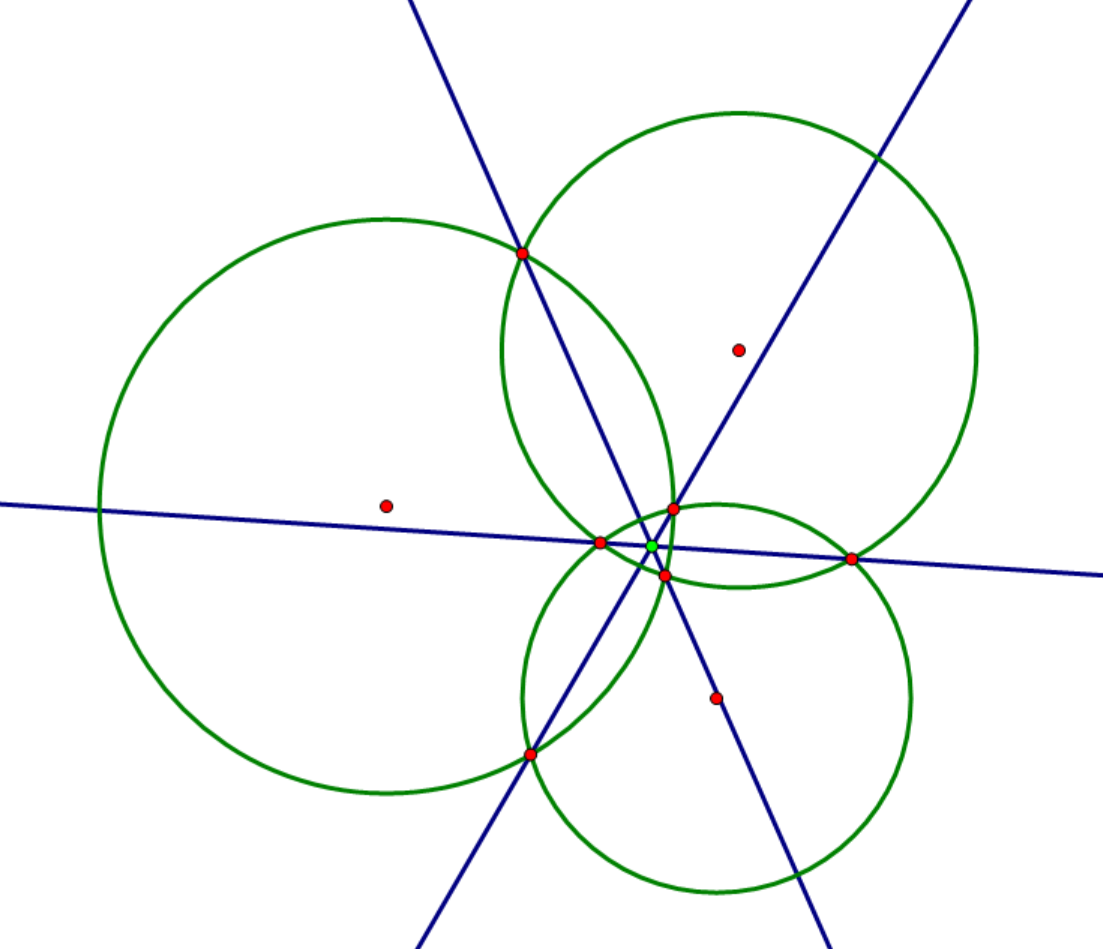
任意三个圆两两根轴要么互相平行（圆心在一条直线上），要么交于一点（即根心）。

证明：运用根轴的性质易证。

圆中张角定理

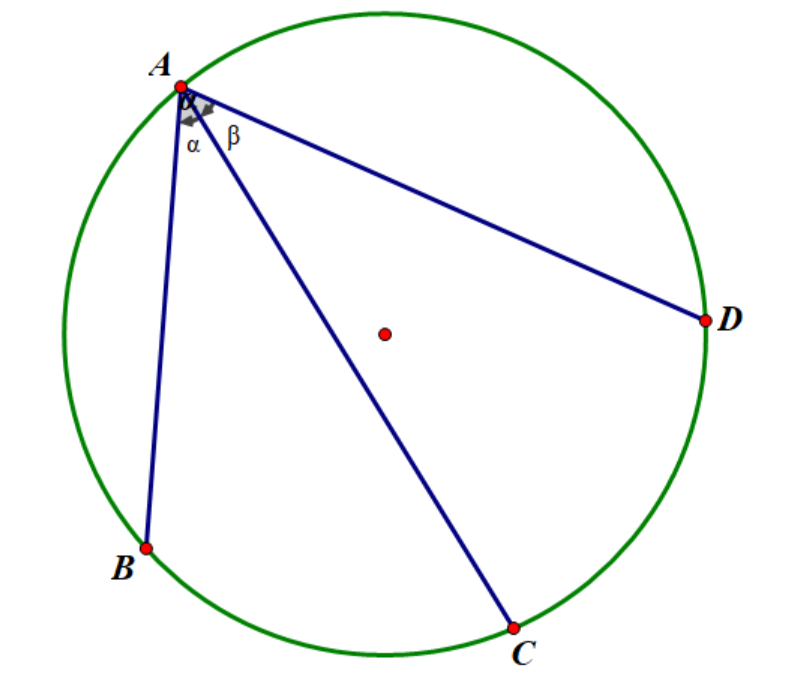
如图， \(AB，AC，AD\) 是圆中三条弦， \(\angle BAC=\alpha,\angle DAC=\beta\) ，则有：\(AB\sin \beta+AD\sin \alpha=AC\sin(\alpha+\beta)\)

证明：正弦定理+Ptolomy 定理。

tricks

Reim 定理

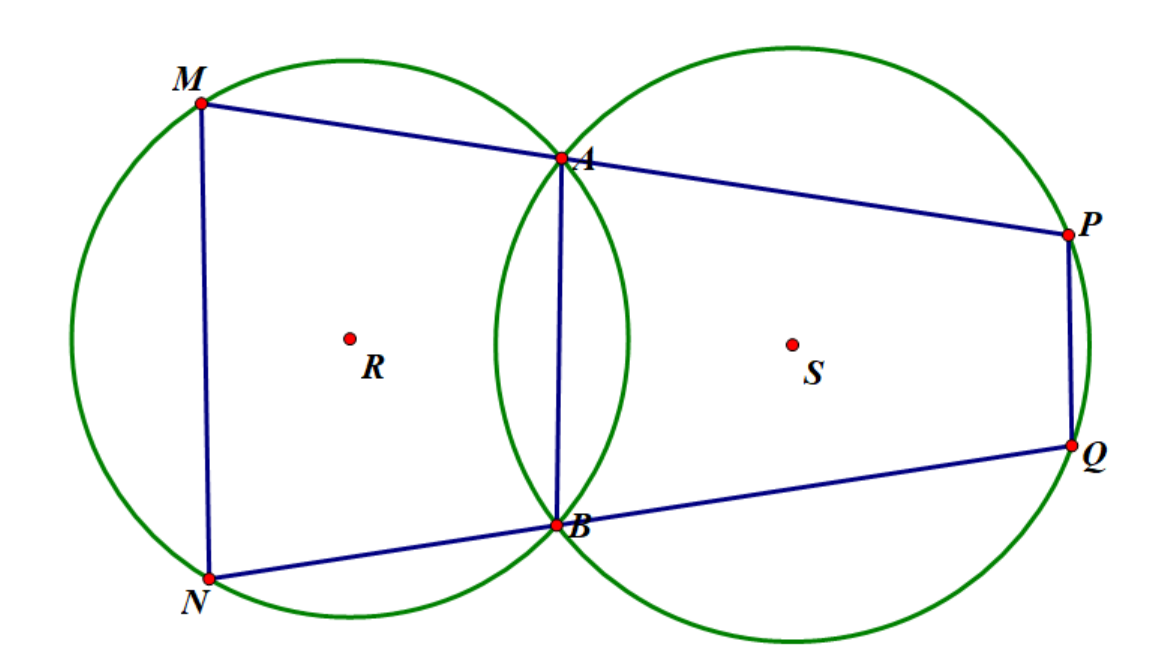
如图， \(AB\) 为两圆公共弦， \(MN\) 为 \(\odot R\) 的一条弦，\(MA\) 与 \(\odot S\) 交于 \(P\)，\(NB\) 与 \(\odot S\) 交于 \(Q\) ，则有 \(MN//PQ\)。

证明：\(\angle NMA=\angle ABQ=180^\circ-\angle APQ,\) 即得 \(MN//PQ\)。

公切点证明 1

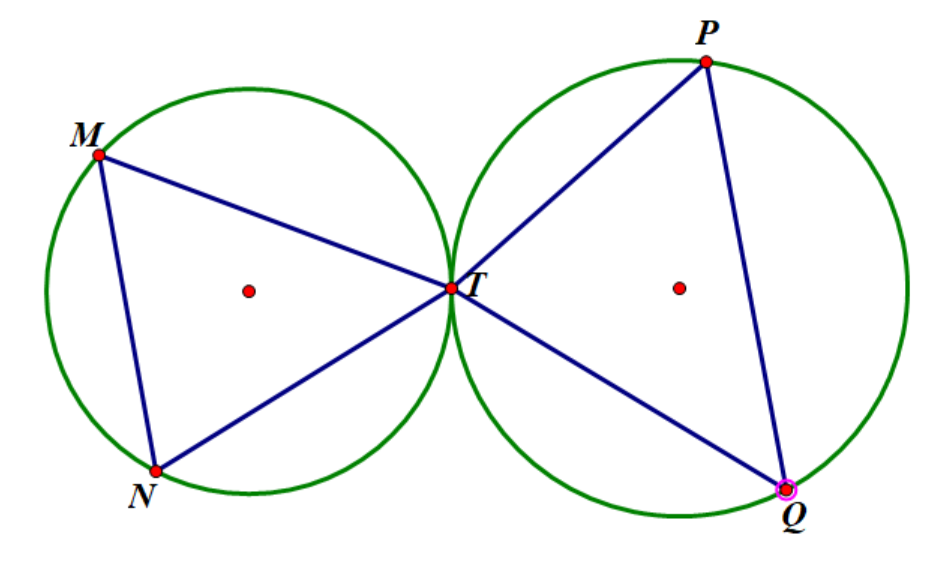
\(\angle MNT+\angle PQT=\angle MTP\) 且 \(T\) 在两圆上时， \(T\) 为两圆公切点

公切点证明 2

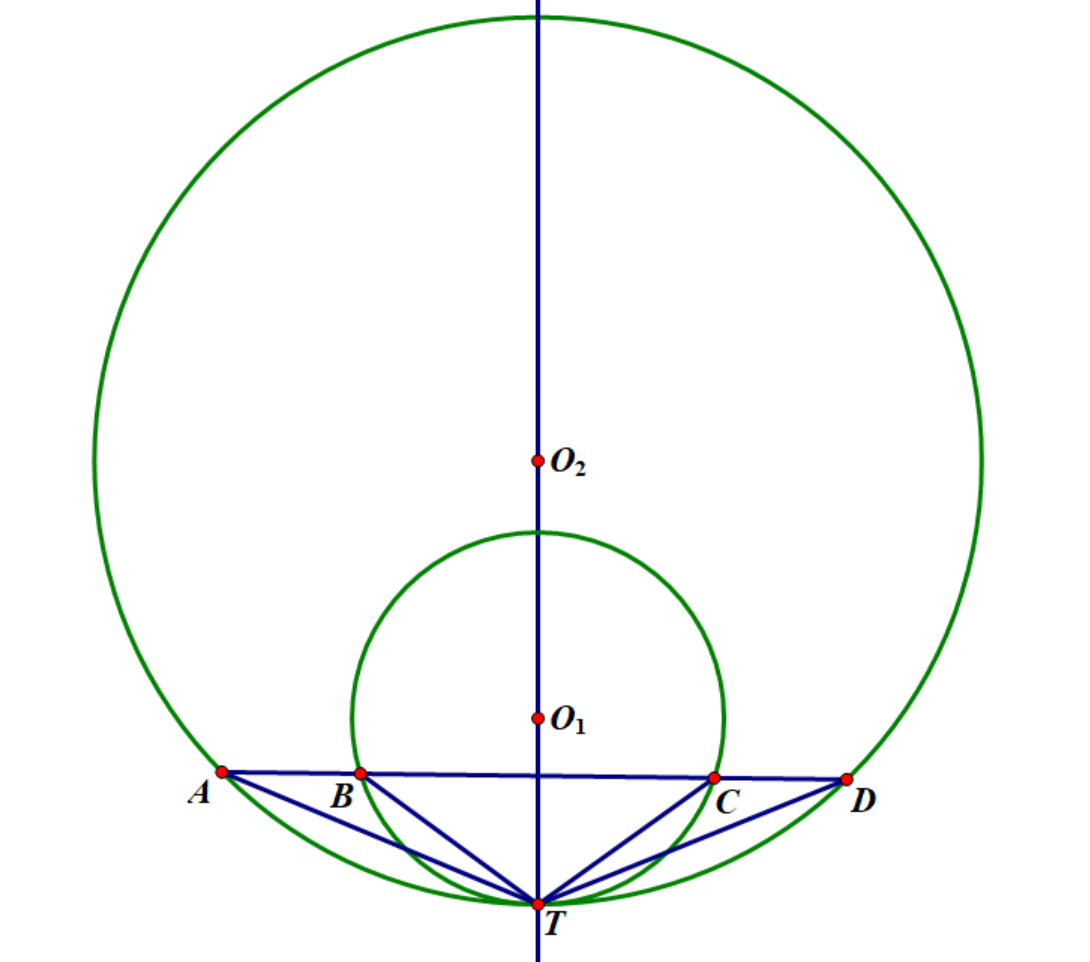
若 \(T\) 为 \(\odot O_1,O_2\) 的公切点，则 \(\angle ATB=\angle CTD\) ，反之亦然。

证明：先化为 \(\angle ATC=\angle BTD\) ，再把每个角分成两部分弧，在小圆上的和在大圆上的，将两部分弧作差，即可推得。

Miquel 点

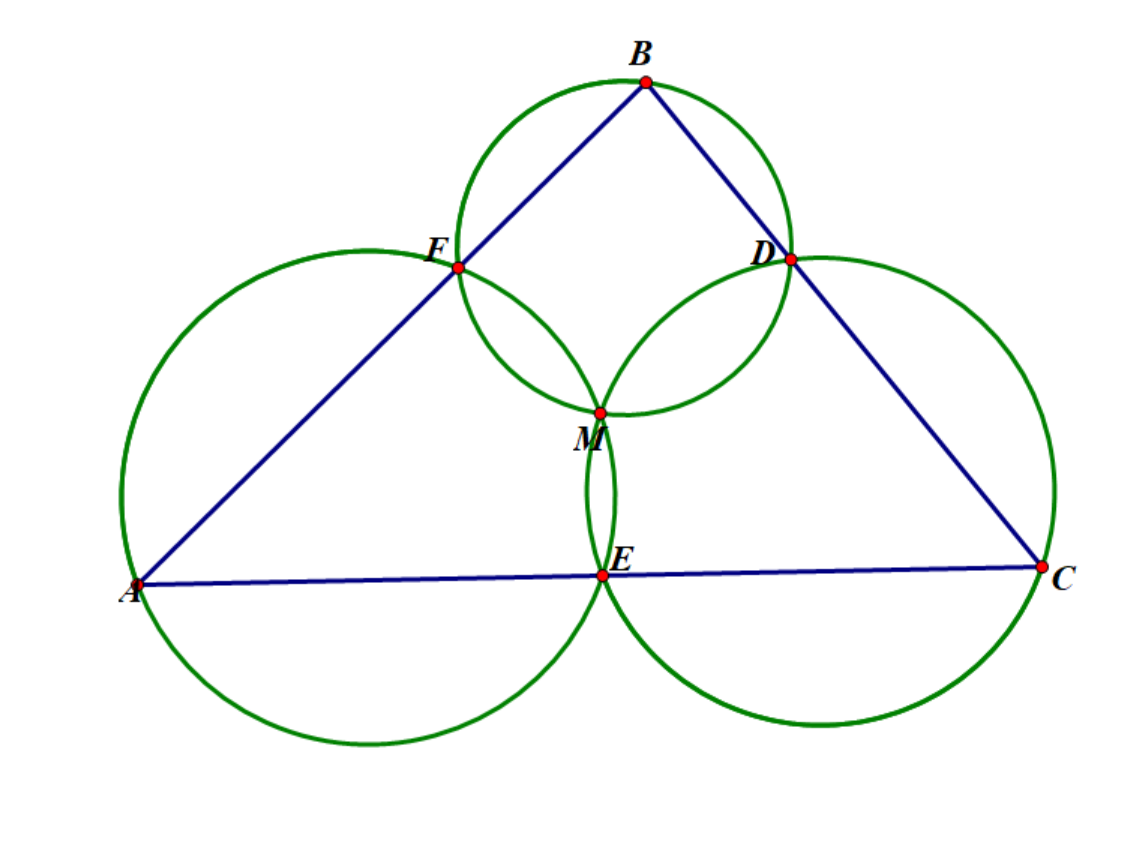
\(\triangle ABC\) 中， \(D、E、F\) 分别在 \(BC、AC、AB\) 上，则 \(\odot(AEF)，\odot(BFD)，\odot(CDE)\) 共点 \(M\) ，被称作 Miquel 点。