数据结构复习:链式二叉树创建和递归遍历

二叉链表中，每个结点除了存储本身的数据外，还应该设置两个指针域left和right，它们分别指向左孩子和右孩子。

当需要在二叉树中经常寻找某结点的双亲，每个结点还可以加一个指向双亲的指针域parent，这就是三叉链表，

下面的两幅图分别就是，二叉链表和三叉链表的数据结构：

          和          

 

二叉树的结构有一些性质来用于帮助我们建树：

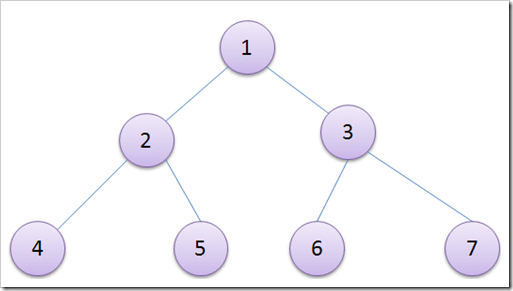
对于一棵满二叉树树中每一个节点，我们可以对他从上到下，从左到右的进行编号i：
(1) 此结点为根结点，无双亲，那么它的索引号为0
(2)  结点i的左孩子为2i + 1，右孩子为2i + 2
(3)  如果i > 0，当i为奇数时，它是其双亲结点的左孩子，它的兄弟为i + 1；当i为偶数时，它是其双亲结点的右孩子，它的兄弟结点为i – 1

代码实现:

(1)二叉树结点类

public class Node {
    // 左孩子
    private Node left;
    // 右孩子
    private Node right;
    // 数据域
    private Object data;

    public Node(Object data) {

        this.data = data;

    }
    
    public Node getLeft() {
        return left;
    }

    public void setLeft(Node left) {
        this.left = left;
    }

    public Node getRight() {
        return right;
    }

    public void setRight(Node right) {
        this.right = right;
    }

    public Object getData() {
        return data;
    }

    public void setData(Object data) {
        this.data = data;
    }

    public String toString() {

        return data.toString();
    }

}

(2)二叉树类

public class BinaryTree {

    private Node head;

    // 用来构造二叉树的字符串
    private String dataStr;

    public Node getHead() {
        return head;
    }
    
    public BinaryTree(String data) {
        dataStr = data;
        // 给这个二叉树 设置头结点数据
        head = new Node(dataStr.charAt(0));
        // 为头结点增加孩子结点
        add(head, 0);

    }

    public void add(Node parent, int index) {
        // 算出左节点的位置
        int leftIndex = 2 * index + 1;
        if (leftIndex < dataStr.length()) {
            if ('#' != dataStr.charAt(leftIndex)) {//'#'表示空结点
                Node leftChild = new Node(dataStr.charAt(leftIndex));
                //添加左孩子
                parent.setLeft(leftChild);
               //递归调用Add方法给左孩子添加孩子节点
                add(parent.getLeft(), leftIndex);
            }
        }
        // 算出右结点的位置
        int rightIndex = 2 * index + 2;

        if (rightIndex < dataStr.length()) {
            if ('#' != dataStr.charAt(rightIndex)) {
                Node rightChild = new Node(dataStr.charAt(rightIndex));
                parent.setRight(rightChild);
                add(parent.getRight(), rightIndex);

            }
        }

    }

    public  void preOrader(Node node) {
        if (node != null) {
            System.out.print(node.getData());
            preOrader(node.getLeft());
            preOrader(node.getRight());

        }
    }

    public  void midOrder(Node node) {
        if (node != null) {

            midOrder(node.getLeft());
            System.out.print(node.getData());
            midOrder(node.getRight());

        }
    }

    public  void backOrder(Node node) {
        if (node != null) {

            backOrder(node.getLeft());

            backOrder(node.getRight());
            System.out.print(node.getData());
        }
    }
   
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree("ABCDE#F");
        tree.preOrader(tree.getHead());//先序遍历
        System.out.println();
        tree.midOrder(tree.getHead());//中序遍历
        System.out.println();
        tree.backOrder(tree.getHead());//后序遍历

    }
}

PS:

本文中的源码下载:binaryTree.zip