BUAA_OO_2022_Unit_1_Summary

目录

• 一、程序结构分析
  • 第一次作业
  • 第二次作业
  • 第三次作业
  • 附：度量分析条目解释
• 二、程序BUG分析
  • 三角函数基本处理
  • 三角函数优化方法
  • 优化出现的问题分析
  • debug前后差异
• 三、自测/互测策略
  • 功能测试
  • 随机测试
  • 阅读代码检查
• 四、心得体会

一、程序结构分析

第一次作业

• 需求简述：

  读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的单变量表达式，输出恒等变形展开所有括号后的表达式。

• 代码构架：

  

  用 Lexer 和 Parser 进行递归下降的表达式内容解析

  用三个类作为解析内容的载体：表达式（Expr）、项（Term）、变量（Variable）

  • 题目中定义的变量因子和常数因子都看作Variable
    • 变量因子：系数为1，指数为x的幂
    • 常数因子：系数为常数数值，指数为0
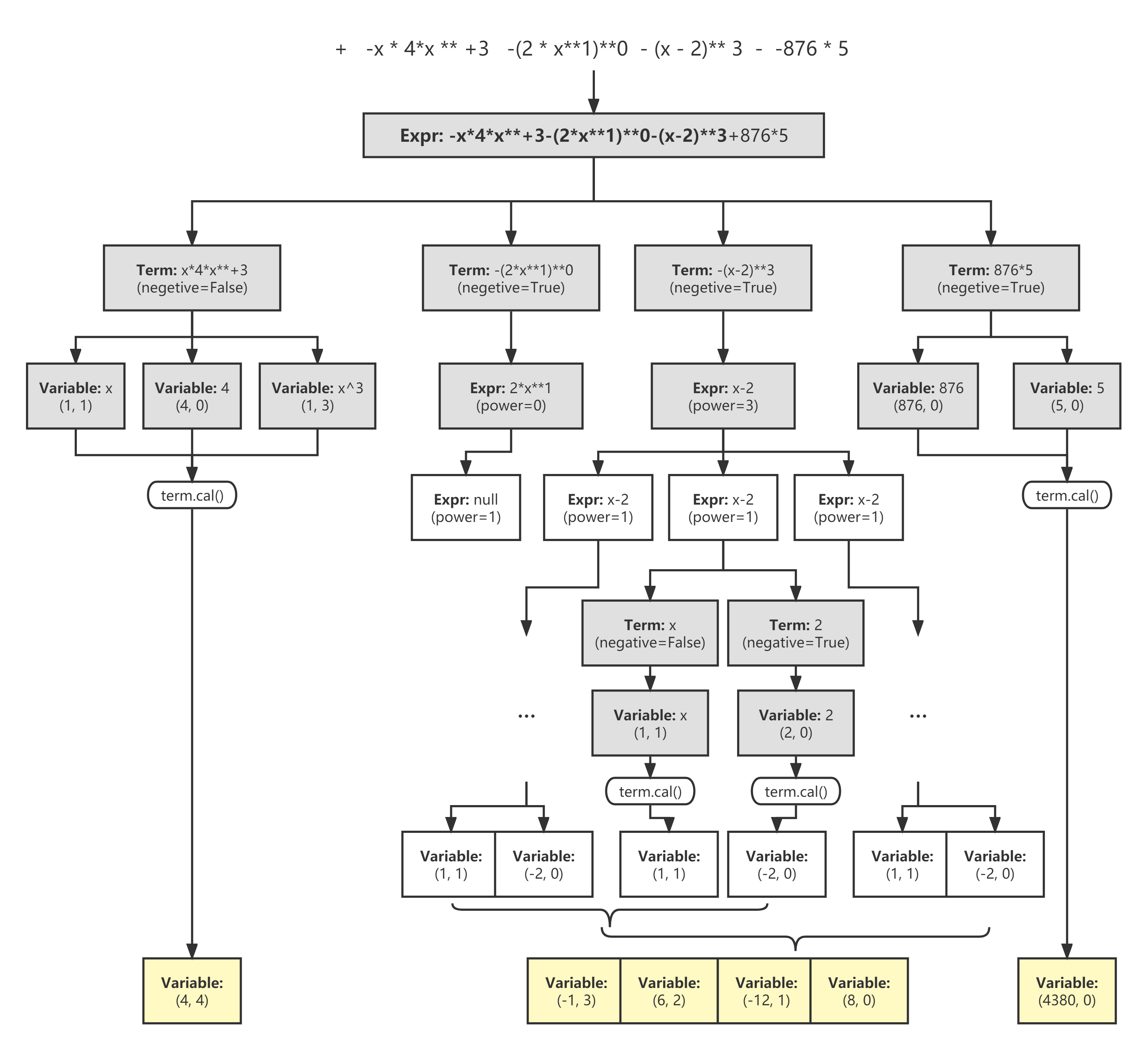
  • 最后的目标是将解析时构建的树，压平至以Variable为单位的数组，使得输出为：Var(eg. 2*x**4) + Var + ...

  处理过程如下：

  

• 规模分析：

  

• 复杂度分析：

  

  method	ev(G)	iv(G)	v(G)
  expr.Expr.addTerm(Term)	1.0	1.0	1.0
  expr.Expr.cal()	1.0	4.0	4.0
  expr.Expr.Expr()	1.0	1.0	1.0
  expr.Expr.getAnss()	1.0	1.0	1.0
  expr.Expr.getCoefficient()	1.0	1.0	1.0
  expr.Expr.getPower()	1.0	1.0	1.0
  expr.Expr.setAnss(HashMap)	1.0	1.0	1.0
  expr.Expr.setCoefficient(BigInteger)	1.0	1.0	1.0
  expr.Expr.setPower(int)	1.0	1.0	1.0
  expr.Expr.toString()	2.0	12.0	12.0
  expr.Term.addFactor(Factor)	1.0	1.0	1.0
  expr.Term.breakBracket()	7.0	7.0	10.0
  expr.Term.breakPower(Factor, int)	1.0	2.0	2.0
  expr.Term.cal()	3.0	3.0	4.0
  expr.Term.calOuter()	3.0	4.0	4.0
  expr.Term.getAnss()	1.0	1.0	1.0
  expr.Term.Term(boolean)	1.0	1.0	1.0
  expr.Variable.getAnss()	1.0	1.0	1.0
  expr.Variable.getCoefficient()	1.0	1.0	1.0
  expr.Variable.getPower()	1.0	1.0	1.0
  expr.Variable.setCoefficient(BigInteger)	1.0	1.0	1.0
  expr.Variable.setPower(int)	1.0	1.0	1.0
  expr.Variable.Variable(boolean, BigInteger, int)	1.0	2.0	2.0
  Lexer.getNumber()	1.0	5.0	5.0
  Lexer.Lexer(String)	1.0	1.0	1.0
  Lexer.next()	2.0	4.0	5.0
  Lexer.peek()	1.0	1.0	1.0
  Lexer.preprocess(String)	1.0	1.0	1.0
  Parser.parseExpr()	1.0	7.0	7.0
  Parser.parseFactor()	2.0	7.0	8.0
  Parser.Parser(Lexer)	1.0	1.0	1.0
  Parser.parseTerm(boolean)	1.0	2.0	2.0
  Unit1.main(String[])	1.0	1.0	1.0
  Total	46.0	80.0	86.0
  Average	1.39	2.42	2.61

第二次作业

• 需求简述：

  读入一系列自定义函数的定义以及一个包含简单幂函数、简单三角函数、简单自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

• 代码构架：

  

  为追求更高的代码复用率，迭代过程中我采用了如下策略：

  （i）依靠正则表达式将自定义函数和求和函数尽数替换成普通表达式后，再进行与第一次作业相同的解析行为。

  （ii）将基本项由 Variable 类换成其子类 Vessel ，仅增加一个装三角函数的容器。

  另外，为了简化合并同类项时的比对流程，我采用如下策略：

  （i）三角相乘合并：以不带指数的部分字符串为 base（如 sin(1)**2 的 sin(1)），并作为容器的 key ，使同 base 的指数相加。

  （ii）基本项相加合并：将除了系数之外的所有内容转化为字符串，并作为容器的 key ，使系数相加。

• 规模分析：

  

• 复杂度分析：

  

  method	ev(G)	iv(G)	v(G)
  DiyFunc.DiyFunc(String)	1.0	4.0	4.0
  DiyFunc.getName()	1.0	1.0	1.0
  DiyFunc.replace(String)	1.0	9.0	10.0
  Lexer.Lexer(String)	1.0	1.0	1.0
  Lexer.getNumber()	1.0	5.0	5.0
  Lexer.getPos()	1.0	1.0	1.0
  Lexer.peek()	1.0	1.0	1.0
  Lexer.preprocess(String)	1.0	1.0	1.0
  Parser.Parser(Lexer)	1.0	1.0	1.0
  Parser.parseExpr()	1.0	5.0	5.0
  Parser.parseTerm(boolean)	1.0	2.0	2.0
  SumFunc.getName()	1.0	1.0	1.0
  Unit1.main(String[])	1.0	5.0	5.0
  Unit1.trans(String, String)	1.0	3.0	3.0
  expr.Expr.Expr()	1.0	1.0	1.0
  expr.Expr.addTerm(Term)	1.0	1.0	1.0
  expr.Expr.cal()	1.0	4.0	4.0
  expr.Expr.getAnss()	1.0	1.0	1.0
  expr.Expr.getPower()	1.0	1.0	1.0
  expr.Expr.setAnss(HashMap)	1.0	1.0	1.0
  expr.Expr.setPower(int)	1.0	1.0	1.0
  expr.Term.Term(boolean)	1.0	1.0	1.0
  expr.Term.addFactor(Factor)	1.0	1.0	1.0
  expr.Term.breakPower(Factor, int)	1.0	2.0	2.0
  expr.Term.calVar()	1.0	6.0	7.0
  expr.Term.getAnss()	1.0	1.0	1.0
  expr.Term.mulTri(HashMap, HashMap)	1.0	3.0	3.0
  expr.Trigono.Trigono(String, String)	1.0	1.0	1.0
  expr.Trigono.getBody()	1.0	1.0	1.0
  expr.Trigono.getName()	1.0	1.0	1.0
  expr.Trigono.getPower()	1.0	1.0	1.0
  expr.Trigono.isNegate()	1.0	5.0	6.0
  expr.Trigono.setPower(int)	1.0	1.0	1.0
  expr.Trigono.toString()	1.0	1.0	1.0
  expr.Variable.Variable(boolean, BigInteger, int)	1.0	2.0	2.0
  expr.Variable.getCoefficient()	1.0	1.0	1.0
  expr.Variable.getPower()	1.0	1.0	1.0
  expr.Variable.setCoefficient(BigInteger)	1.0	1.0	1.0
  expr.Variable.setPower(int)	1.0	1.0	1.0
  expr.Vessel.Vessel(BigInteger, int, HashMap)	1.0	1.0	1.0
  expr.Vessel.getTris()	1.0	1.0	1.0
  Lexer.next()	2.0	6.0	7.0
  Parser.parseFactor()	2.0	9.0	10.0
  expr.Expr.toString()	2.0	17.0	17.0
  SumFunc.replace(String)	3.0	10.0	11.0
  expr.Term.cal()	3.0	3.0	4.0
  expr.Term.breakBracket()	7.0	7.0	10.0
  expr.Vessel.tris2Str()	7.0	8.0	11.0
  Total	67.0	143.0	156.0
  Average	1.40	2.98	3.25

第三次作业

• 需求简述：

  读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用以及求和函数的表达式，输出恒等变形展开所有括号后的表达式。

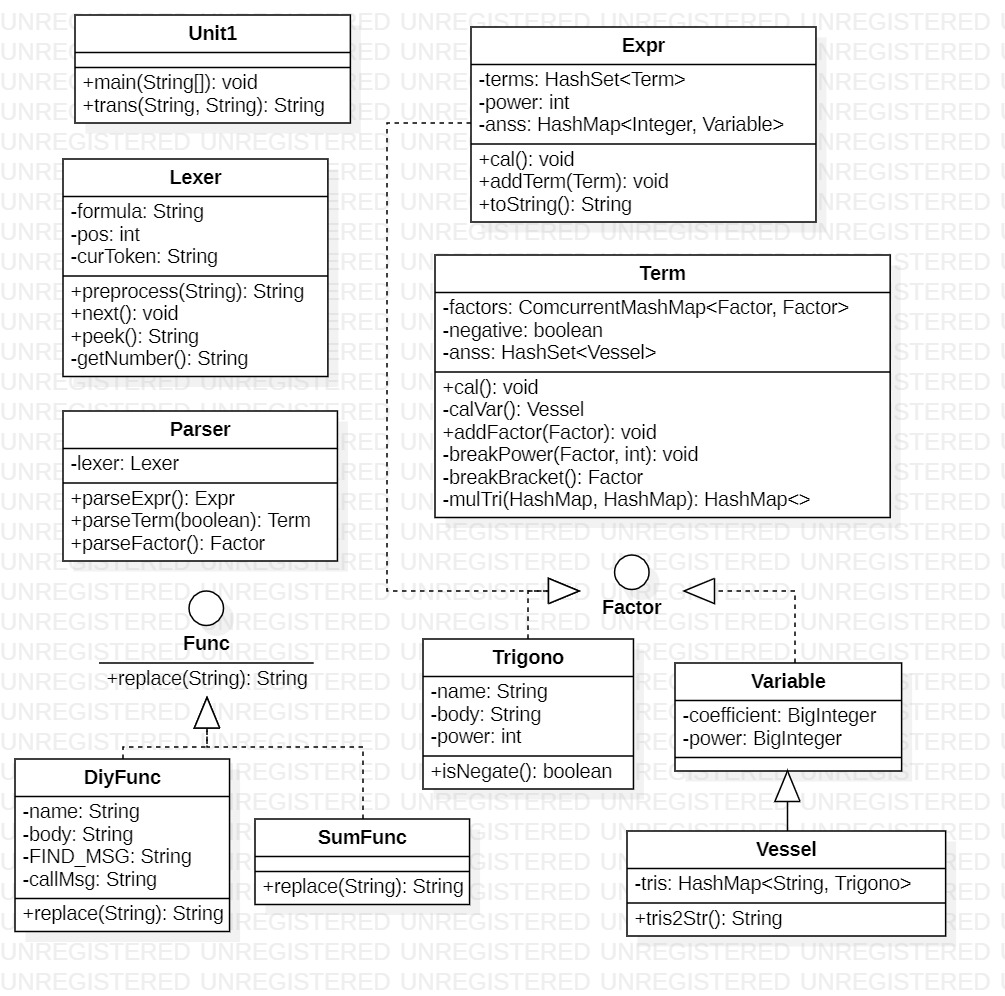
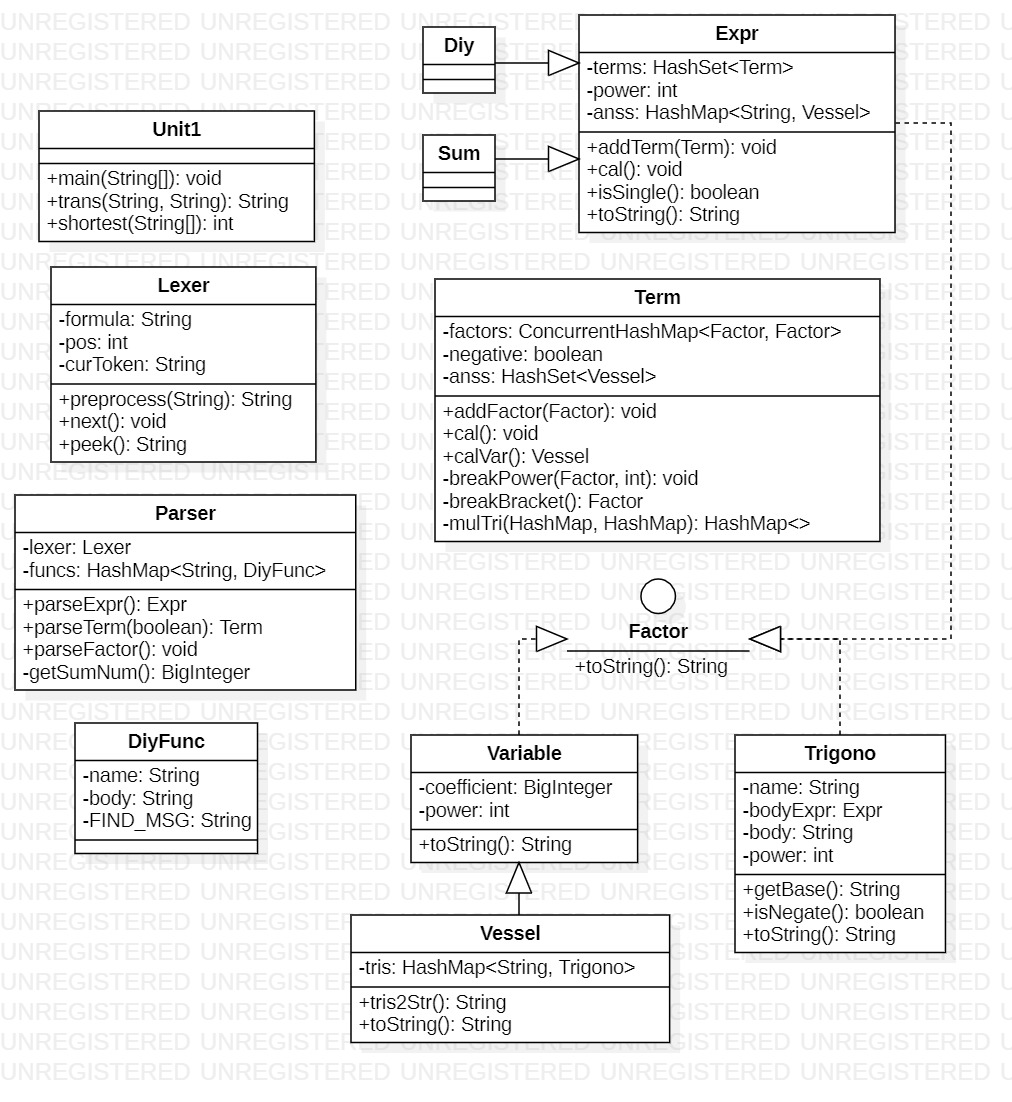
• 代码构架：

  

  实在受不了第二次作业里正则替换 SumFunc 和 DiyFunc 时不断出现的稀奇古怪的bug，我进行了函数展开部分的重构。其中，自定义函数的实参替换、求和函数的展开逻辑仍复用上次作业的代码，因此工作量并不大。

  另外，为解决三角函数内的括号问题，我设计了表达式因子的 isSingle 判断函数，有效杜绝了暴力加括号的优化摆烂行为。

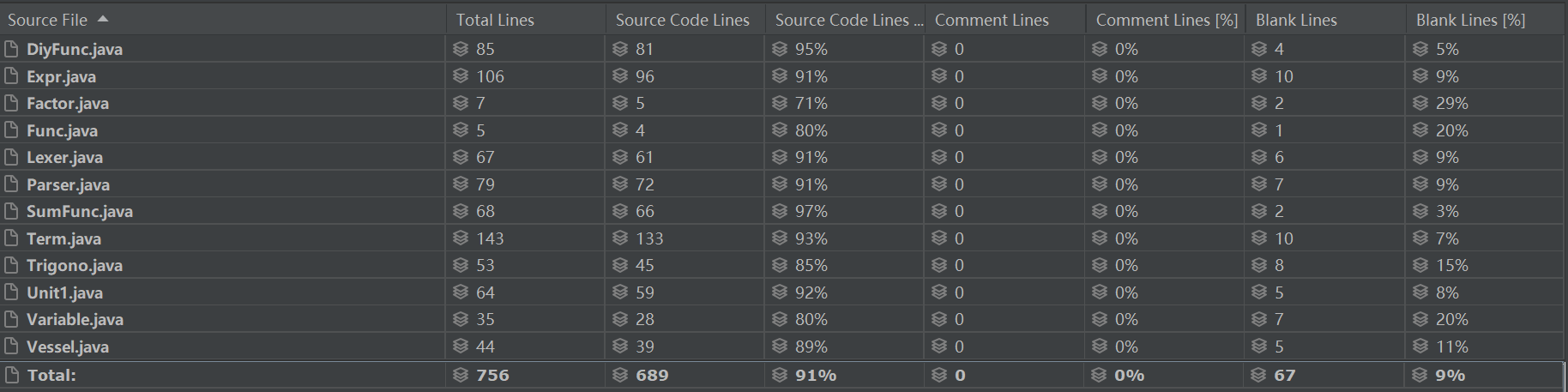
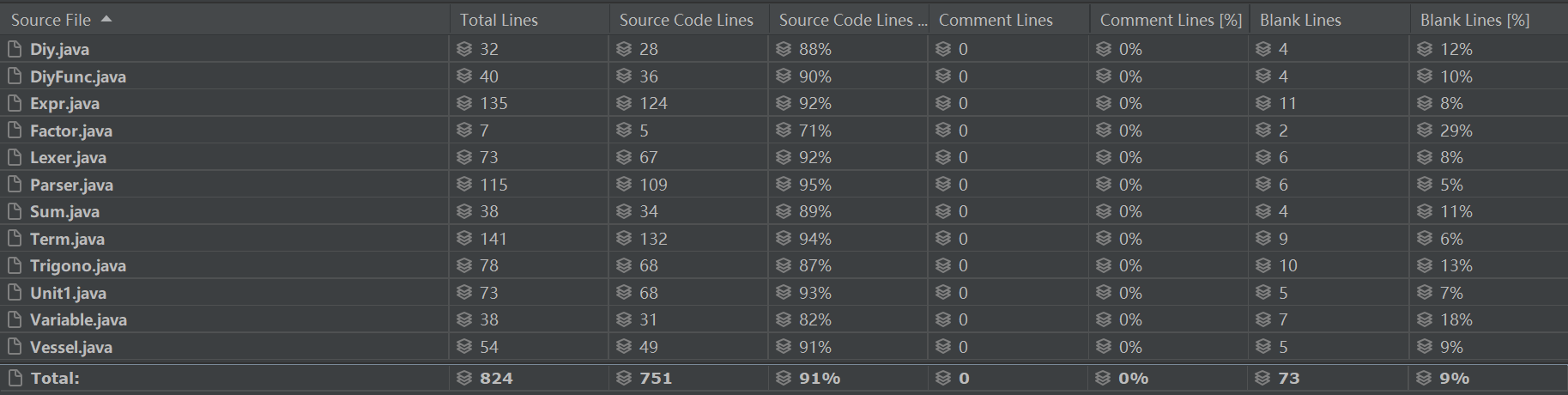
• 规模分析：

  

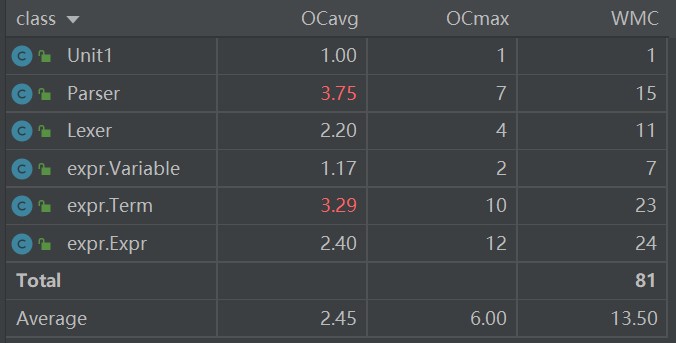
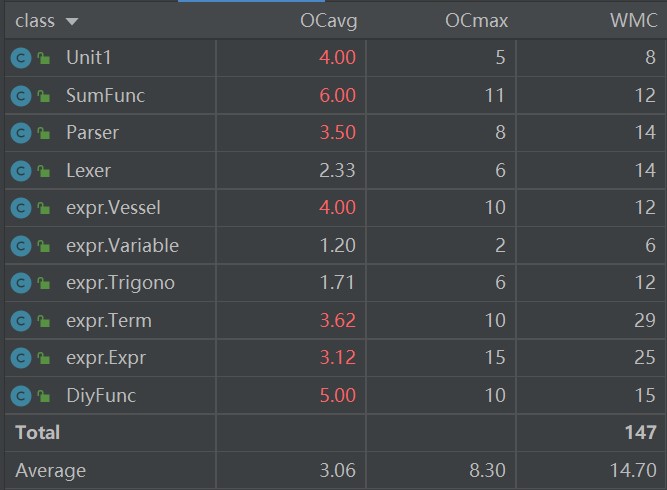
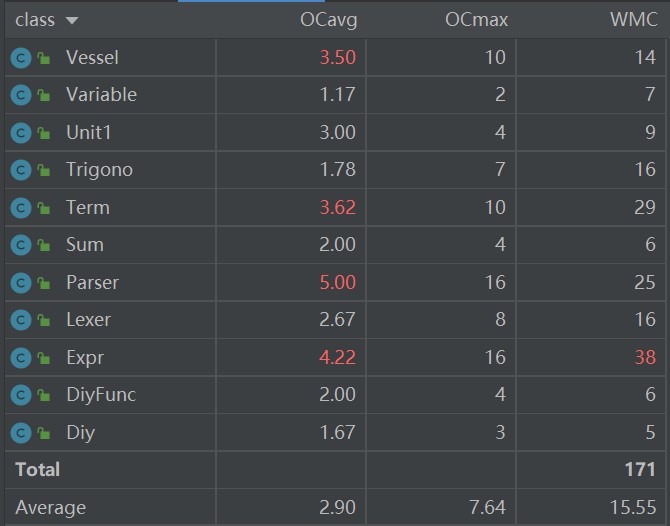
• 复杂度分析：

  

  method	ev(G)	iv(G)	v(G)
  Diy.Diy(String, HashMap, HashMap)	1.0	3.0	3.0
  Diy.getPower()	1.0	1.0	1.0
  Diy.setPower(int)	1.0	1.0	1.0
  DiyFunc.DiyFunc(String)	1.0	4.0	4.0
  DiyFunc.getBody()	1.0	1.0	1.0
  DiyFunc.getName()	1.0	1.0	1.0
  Expr.Expr()	1.0	1.0	1.0
  Expr.addTerm(Term)	1.0	1.0	1.0
  Expr.cal()	1.0	4.0	4.0
  Expr.getAnss()	1.0	1.0	1.0
  Expr.getPower()	1.0	1.0	1.0
  Expr.setAnss(HashMap)	1.0	1.0	1.0
  Expr.setPower(int)	1.0	1.0	1.0
  Expr.toString()	1.0	18.0	18.0
  Lexer.Lexer(String)	1.0	1.0	1.0
  Lexer.getNumber()	1.0	5.0	5.0
  Lexer.getPos()	1.0	1.0	1.0
  Lexer.peek()	1.0	1.0	1.0
  Lexer.preprocess(String)	1.0	1.0	1.0
  Parser.Parser(Lexer, HashMap)	1.0	1.0	1.0
  Parser.getSumNum()	1.0	3.0	3.0
  Parser.parseExpr()	1.0	5.0	5.0
  Parser.parseTerm(boolean)	1.0	2.0	2.0
  Sum.Sum(BigInteger, BigInteger, String)	1.0	4.0	4.0
  Sum.getPower()	1.0	1.0	1.0
  Sum.setPower(int)	1.0	1.0	1.0
  Term.Term(boolean)	1.0	1.0	1.0
  Term.addFactor(Factor)	1.0	1.0	1.0
  Term.breakPower(Factor, int)	1.0	2.0	2.0
  Term.calVar()	1.0	6.0	7.0
  Term.getAnss()	1.0	1.0	1.0
  Term.mulTri(HashMap, HashMap)	1.0	3.0	3.0
  Trigono.Trigono(String, Expr)	1.0	2.0	2.0
  Trigono.Trigono(String, String)	1.0	1.0	1.0
  Trigono.getBase()	1.0	1.0	1.0
  Trigono.getBody()	1.0	1.0	1.0
  Trigono.getName()	1.0	1.0	1.0
  Trigono.getPower()	1.0	1.0	1.0
  Trigono.setPower(int)	1.0	1.0	1.0
  Trigono.toString()	1.0	1.0	1.0
  Unit1.main(String[])	1.0	2.0	2.0
  Unit1.shortest(String[])	1.0	3.0	3.0
  Variable.Variable(boolean, BigInteger, int)	1.0	2.0	2.0
  Variable.getCoefficient()	1.0	1.0	1.0
  Variable.getPower()	1.0	1.0	1.0
  Variable.setCoefficient(BigInteger)	1.0	1.0	1.0
  Variable.setPower(int)	1.0	1.0	1.0
  Variable.toString()	1.0	1.0	1.0
  Vessel.Vessel(BigInteger, int, HashMap)	1.0	1.0	1.0
  Vessel.getTris()	1.0	1.0	1.0
  Lexer.next()	2.0	10.0	13.0
  Parser.parseFactor()	2.0	20.0	22.0
  Vessel.toString()	2.0	2.0	2.0
  Term.cal()	3.0	3.0	4.0
  Trigono.isNegate()	3.0	7.0	9.0
  Unit1.trans(String, String)	3.0	4.0	4.0
  Term.breakBracket()	7.0	7.0	10.0
  Vessel.tris2Str()	7.0	8.0	11.0
  Expr.isSingle()	12.0	13.0	17.0
  Total	91.0	176.0	195.0
  Average	1.54	2.98	3.31

附：度量分析条目解释

• OC：类的非抽象方法圈复杂度，继承类不计入
• WMC：类的总圈复杂度
• ev(G)：非抽象方法的基本复杂度，用以衡量一个方法的控制流结构缺陷，范围是 [1, v(G)]
• iv(G)：方法的设计复杂度，用以衡量方法控制流与其他方法之间的耦合程度，范围是 [1, v(G)]
• v(G)：非抽象方法的圈复杂度，用以衡量每个方法中不同执行路径的数量

二、程序BUG分析

• 第一次、第三次作业在公测和互测中均无bug
• 第二次作业仅被发现一个bug，但被强侧和互测疯狂橄榄

该bug出现在优化 sin(0) 的部分。

三角函数基本处理

三角合并后（如 sin(x)*sin(x) --> sin(x)**2 ），将所有三角函数转化为字符串，例如基本项 2*x*sin(x)*cos(1) 内存在一个字符串 sin(x)*cos(1) 。转化字符串的过程中，遇到一个三角则追加 *xxx(?)**? 。若指数为0，跳过该因子。三角容器遍历结束后删除字符串首字符 * 。

三角函数优化方法

遇到 cos(0) 时跳过该因子，遇到 sin(0) 时将整个字符串的首字符替换为 00 作为零标记。倘若最后字符串以 00 开头，则将字符串第1到最后的字符删去，仅保留一个 0 字符，告诉最终得答案的程序：“该基本项为0”。

优化出现的问题分析

这个优化方法是可行的，但我忽略了2个细节：

​ ① 如果基本项仅有 sin(0) ，转化过程中字符串为 00 ，删除首字符后为 0 。此时又要删除第1到最后的字符，但字符串已经没有“第一个字符”了，out of index。

​ ② sin(0) 判断与指数为0的判断写成了并行，甚至 sin(0) 在0次幂之前，导致出现 sin(0)**0 时同样会出现 sin(0) 的报错。

debug前后差异

因为只是判断条件处的考虑不周，debug过程中只是增加了少量 if-else 语句，代码体量和复杂度基本无变化。

三、自测/互测策略

功能测试

• 数据类型分层：粒子＆组合
• 关注覆盖度：讨论最小粒子的所有可能情况
• 数据不需要复杂：仅进行一层排列组合，其余交由随机测试

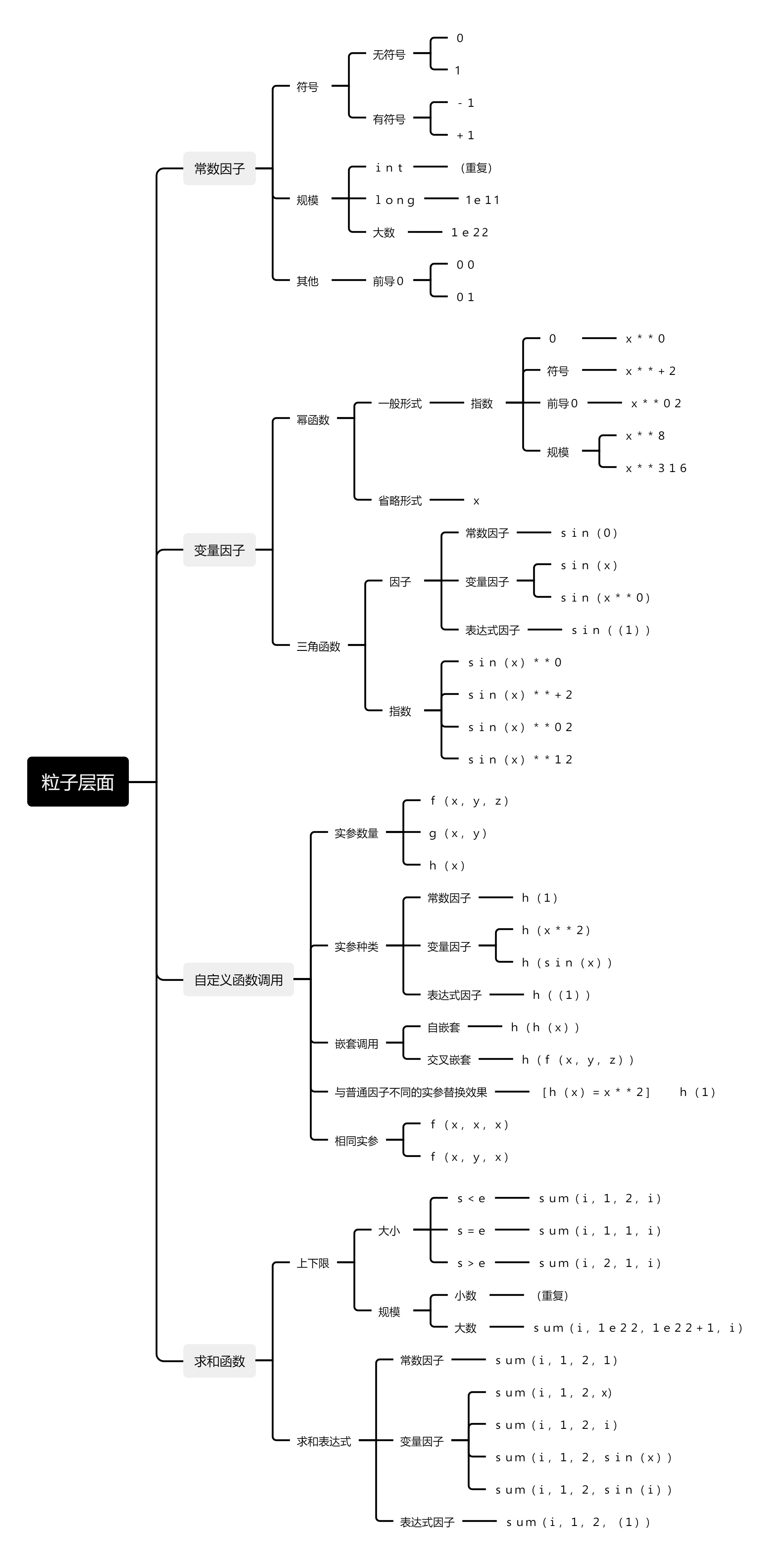
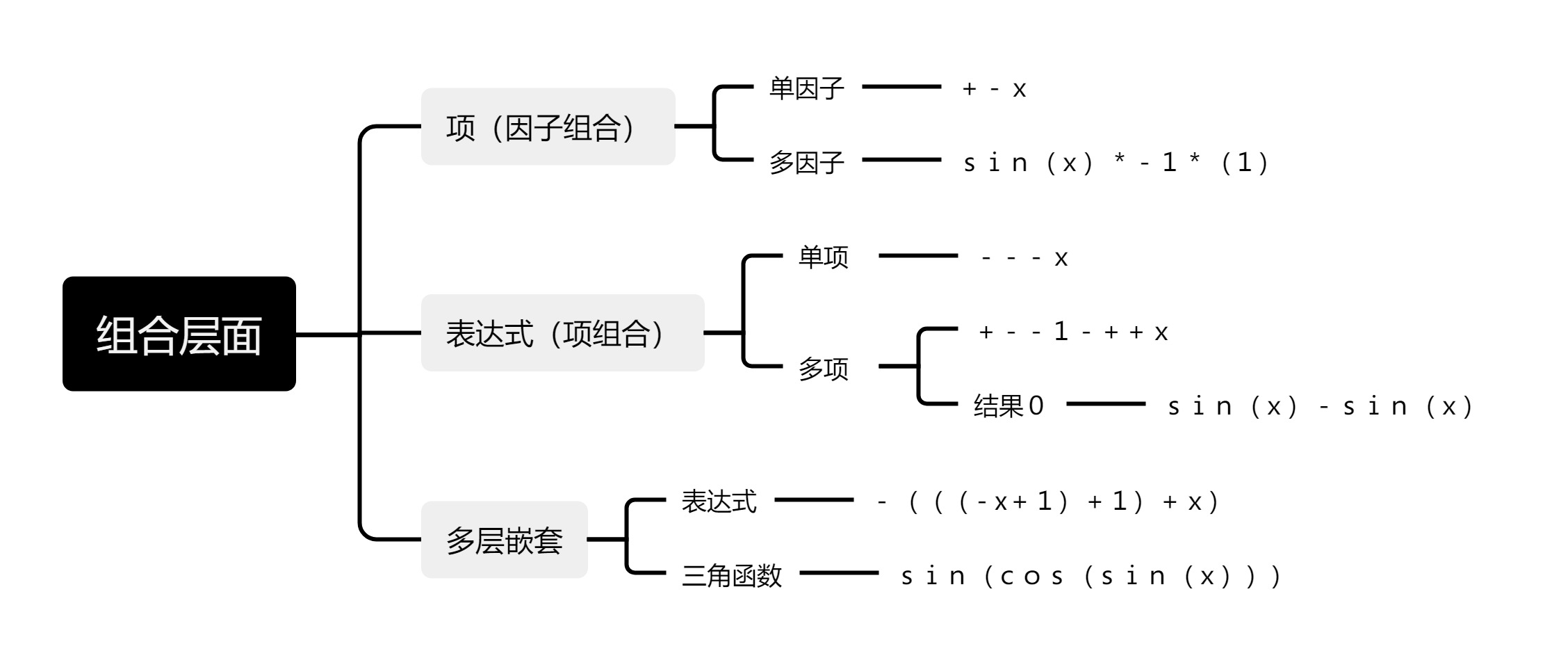
随机测试

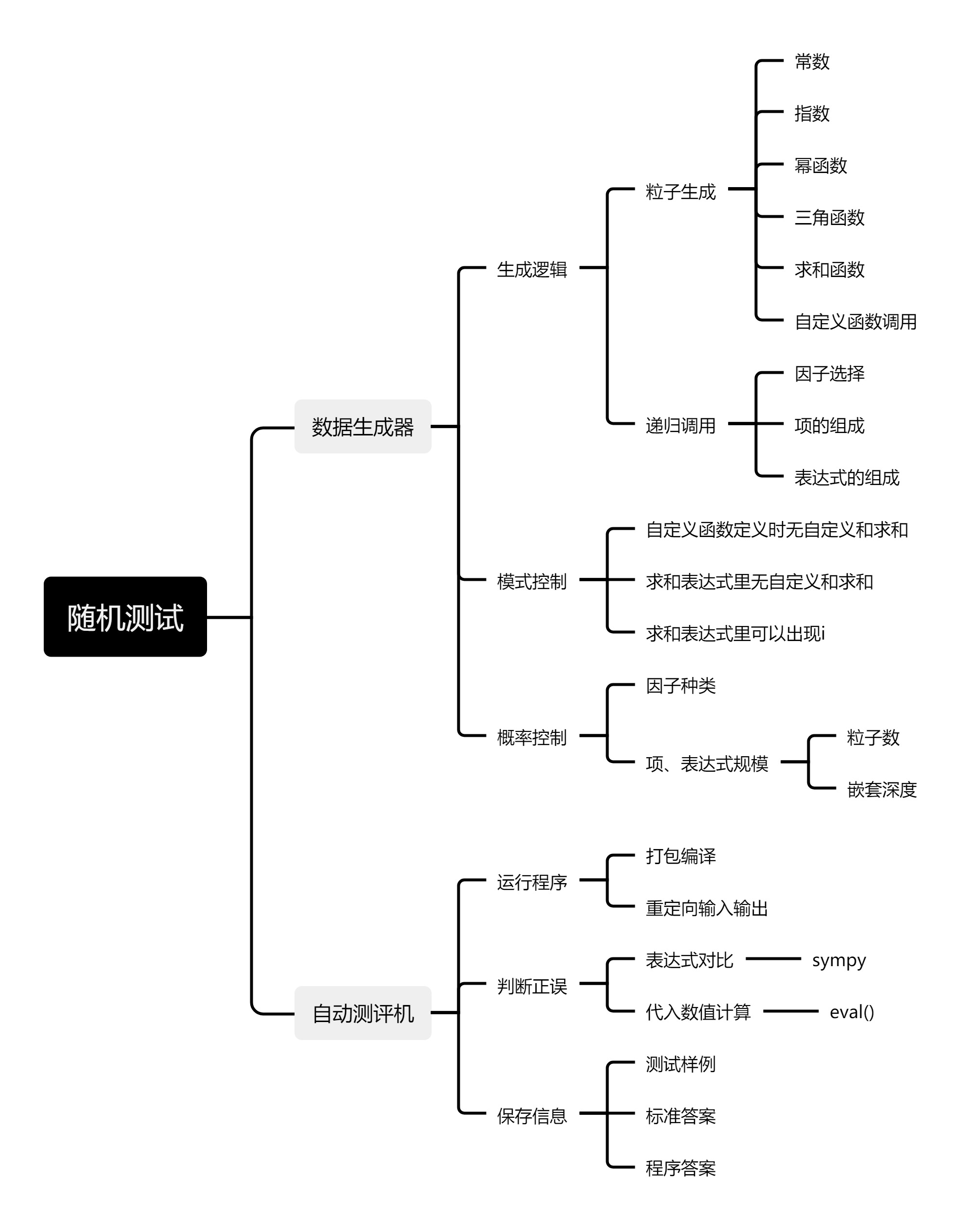
阅读代码检查

由于本单元作业给出了明确的样例数据形式化表述，我充分（盲目）相信我的测评机，所以并没有仔细阅读代码，只是粗略检查了每份代码中使用正则表达式的部分，但没有收获。

每次互测结束之后，我都查看了屋里hack成功的所有样例。第一、二次互测中，没有我没刀中的bug；第三次我没找到的bug都是 wrong format 的问题（如 cos(sin(x)*cos(x)) ），这的确是我的代值测评机的缺陷。

四、心得体会

• 面向对象思维

  在 pre2 的训练和寒假阅读的某项目代码的帮助下，我脑子里根深蒂固的面向过程思想已经向面向对象方向迈进了一大步。

  然而，细究第一单元的程序代码，还是能发现不少面向过程的痕迹，没有做好类的自我管理。这里讲的思想意识上的欠缺是第一周写作业时的硬伤。而我因为从头到尾没有进行大幅度的重构，且为了复用已写好的类和方法，没有把陆续增进的面向对象理解（课上讲解、DL s' 帖子阅读）充分体现在代码中。

• 可迭代性

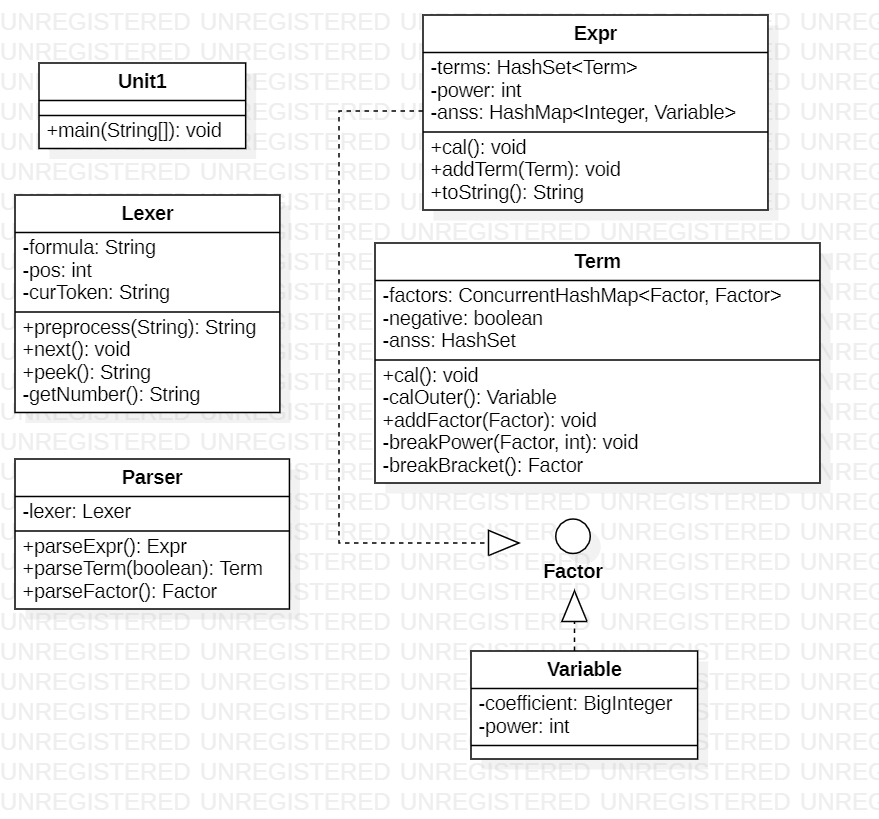
  三次作业中，我有意识注意代码的可迭代性。实际上也做到了这一点，大幅度的代码复用可以证明。但从这一单元的代码成品来看，仅限于“能做到”。下面用一张图生动形象地展示一下我的迭代结构：

  

• 测试

  这是我第一次从头到尾自己操刀写自动测评程序。第一版写好之后特别特别兴奋，恨不得开着测评机从早跑到晚，只为显示“我实现了自动测试，我可以一边测试一边睡觉了！”

  因为有测评机，互测环节成为了一个期待项，平时很难醒来的早八到了周日都不是问题，hack得特别起劲。第一、二次互测屋里都是我的刀最狠（希望不会被线下hack，延时害怕了），成就感upup。

  自动的东西从来都很对我胃口（因为懒惰），可以“一劳永逸”——花点时间写测评机，后续快乐 = 周日开着7个 cmd 开始各测 5000 条然后去补觉（bushi