Mathematica 随笔

用用这个Live Writer写篇文章，写篇Mathematica的随笔吧。

• 函数定义

f[x_] := Sin[x] / x

查看定义
？f

• 绘制函数图形

接上，

Plot[f[x], {x, -10 Pi, 10 Pi}, PlotRange -> {-0.5, 1}]

 

 

清除函数定义

Clear[f]

• 分段函数定义

MyAbs[x_] := Piecewise[{{x, x >= 0}, {-x, x < 0}}]

绘制其图形

Plot[MyAbs[x], {x, -30, 30}]

再来一个（输入方法为：ESC+P+W+ESC 产生大括号，Ctrl + 或者,CTRL + Enter   产生分段输入，使用Ctrl + Enter 增加新的行，即分段定义）

得到其输入方式

MySign[x] // InputForm

得到其常规数学表示方式

MySign[x] // TraditionalForm

分段函数还可以用If之类的定义方式，但不如Piecewise来的标准，如
Incr[x_] := If[x > 1, x, If[x < 0, 0, x^2]]

• 数列及通项的定义

数列前n项可以由Table生成，实际上生成了一个行向量

Table[(x + 1)/x, {x, 1, 100, 1}]

当然可以直接定义一个数列的前n项，用大括号括起来就行了，像个一维行向量，如写出Fibonacci的前几项

an = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89}

让Mathematica帮我们找出产生该数列的一个简单通项

FindSequenceFunction[an, n]

结果竟然、果然是

像上面的那个Table生成的数列也可以给出一个通项，自己try。

 

数列又称整标函数，所以通项与函数的定义类似，例如我们自己定义一下卢卡斯数(Lucas)

Ln[1] = 1
Ln[2] = 3
Ln[n_] := Ln[n - 1] + Ln[n - 2]  

看看前n项

Table[Ln[n], {n,1, 25}]

找出通项

FindSequenceFunction[%,n]

PS: 求解递推方程 Fibonacci

RSolve[{a[n] == a[n - 1] + a[n - 2], a[1] == 1, a[2] == 1}, a[n], n]

• 绘制数列图形

ListPlot[Table[(x + 1)/x, {x, 1, 30}], PlotRange -> {0, 2.5}, PlotStyle -> PointSize[0.02]]

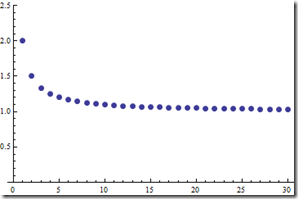
把这些点连起来的话，使用ListLinePlot

ListLinePlot[Table[(x + 1)/x, {x, 1, 30}], PlotRange -> {0, 2.5}]

 

当没有指定 x  的数值时，ListPlot 或 ListLinePlot 的 x 轴默认使用步长为1的整数绘制，指定 x 的值是用一个两列的矩阵，如

xn = {{1, 1}, {2, 3}, {3, 5}, {5, 7.2}, {6, 8.1}, {9, 10.1}, {12, 15.3}, {13, 19.8}};
ListPlot[xn, PlotRange -> {{0, 15}, {0, 20}}]

 

自己输入这些数值显然比较麻烦哈，可以使用 ReadList 或 Import 等函数来导入外部数据。

• 从外部读入数据

假定我们的数据存在 D 盘的根目录下，文件名为 TestData.txt ，我们为了方便，设定工作目录：

SetDirectory[“D:\\”]

让我们先看一下这个文件的内容：

FilePrint[“TestData.txt”]

如下所示：

1    2.5     3.7     9.8
2    3.7     2.7     9.8
3    6.9     2.1     10.33
4    9.8     3.88    21.66
5    34.7    67.22    78.99
6    89.0    89.66    78.88
7    72.0    23.8    23.45

使用ReadList读入数据（为了方便查看，读入后将其表示为矩阵的形式）：

MyList = ReadList["TestData.txt", {Number, Number, Number, Number}]

 

我们假定第一列为我们的仿真步数 n ，第二、三、四列为x、y、z坐标，现在我们想画出 n – z 图形

从上面的数据中提取感兴趣的数据：

DataNZ = Transpose[{MyList[[All, 1]], MyList[[All,  4]]}]

{{1, 9.8}, {2, 9.8}, {3, 10.33}, {4, 21.66}, {5, 78.99}, {6, 78.88}, {7, 23.45}}

绘出图形：

ListLinePlot[DataNZ, PlotRange -> {{0, 7}, {0, 99}}]

如果我们的数据为二进制格式，需要使用 BinaryReadList 等函数，暂时先不说了。

另外还有许多OpenRead、Close、Skip等文件操作函数。