二维前缀和

https://vjudge.net/problem/HDU-6336

一道规律题，只不过这个规律有点难发现，先是依据题目把矩阵打出来发现是这样的

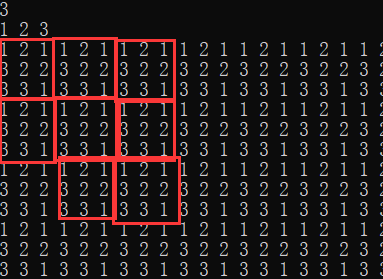
发现当L是奇数时按照L* L的小矩阵这样一直重复来的

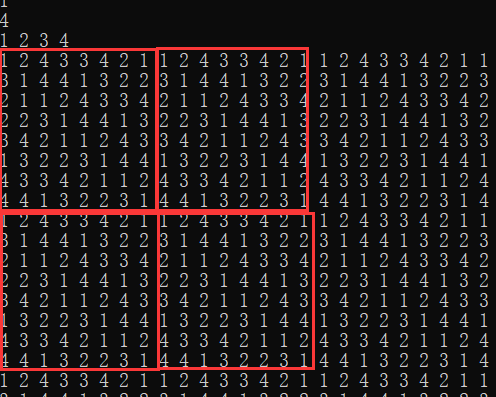
当L是偶数时按照 2L * 2L这样的小矩阵一直重复来的，这样不管奇偶都可以用2L * 2L做循环节

然后就可以用二维前缀和来计算，代码如下：

const int maxn = 100+7;
int a[15],L;
ll m[maxn][maxn];  //原矩阵
ll M[maxn][maxn];  //前缀和矩阵

void init()
{
    int cur=0;
    for(int i = 0; i < maxn; i++) {
        for(int j = 0; j <= i; j++) {
            m[j][i - j] = a[cur];
            cur = (cur + 1) % L;
        }
    }
    for(int i = 1; i <= 2 * L; i++) {
        for(int j = 1; j <= 2 * L; j++) {
            M[i][j]=m[i-1][j-1];
        }
    }
    for(int i = 1; i <= 2 * L; i++) {
        for(int j = 1; j <= 2 * L; j++) {
            M[i][j] += M[i - 1][j] + M[i][j - 1] - M[i - 1][j - 1];
        }
    }
    /*
    for(int i = 0; i < 30; i++) {
        for(int j = 0; j < 30; j++) {
            cout<<m[i][j]<<' ';
        }
        cout<<endl;
    }
    */
}

ll getsum(int x1, int y1, int x2, int y2)
{
    return M[x2][y2] - M[x1 - 1][y2] - M[x2][y1 - 1] + M[x1 - 1][y1 - 1];
}

ll calc(int x, int y)
{
    ll t1 = x / (2 * L);
    ll t2 = y / (2 * L);
    ll ans = 1LL * t1 * t2 * getsum(1, 1, 2 * L, 2 * L);
    ans += 1LL * t1 * getsum(1, 1, 2 * L, y % (2 * L) + 1);
    ans += 1LL * t2 * getsum(1, 1, x % (2 * L) + 1, 2 * L);
    ans += 1LL * getsum(1, 1, x % (2 * L) + 1, y % (2 * L) + 1);
    return ans;
}

int main()
{
    int t;
    cin>>t;
    while(t--) {
        cin>>L;
        for(int i = 0; i < L; i++) cin>>a[i];
        init();
        int q;
        cin>>q;
        while(q--) {
            int x1,y1,x2,y2;
            cin>>x1>>y1>>x2>>y2;
            //x1++; y1++; x2++; y2++;
            ll ans = calc(x2, y2) - calc(x1 - 1, y2) - calc(x2, y1 - 1) + calc(x1 - 1, y1 - 1);
            cout<<ans<<'\n';
        }
    }
    return 0;
}