数据结构复习纲要

前言

如题，这是一个纲要

第六章 链表

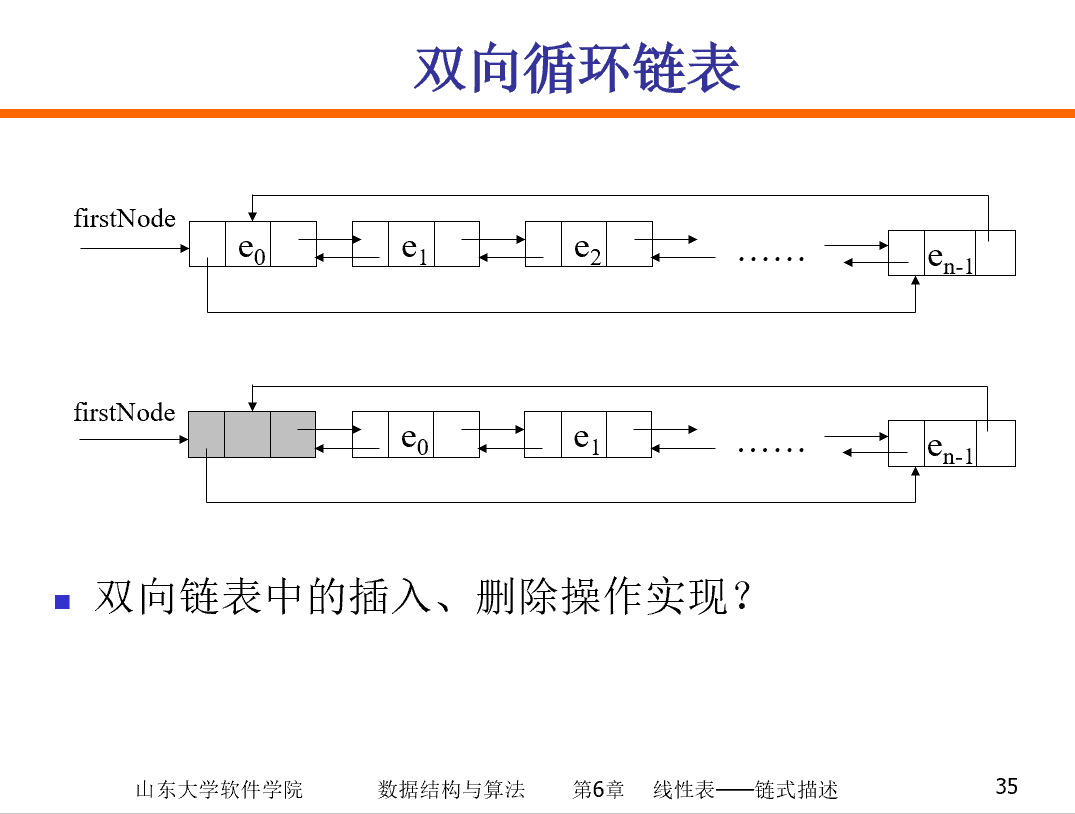
双向循环链表

image

第七章 数组和矩阵

·矩阵中地址和位置的换算

·特殊矩阵如何用一维映射函数存储
比如：
image

第八章 栈

·进出栈的不可能操作
image

补充：
单调栈的两种算法实现

第九章 队列

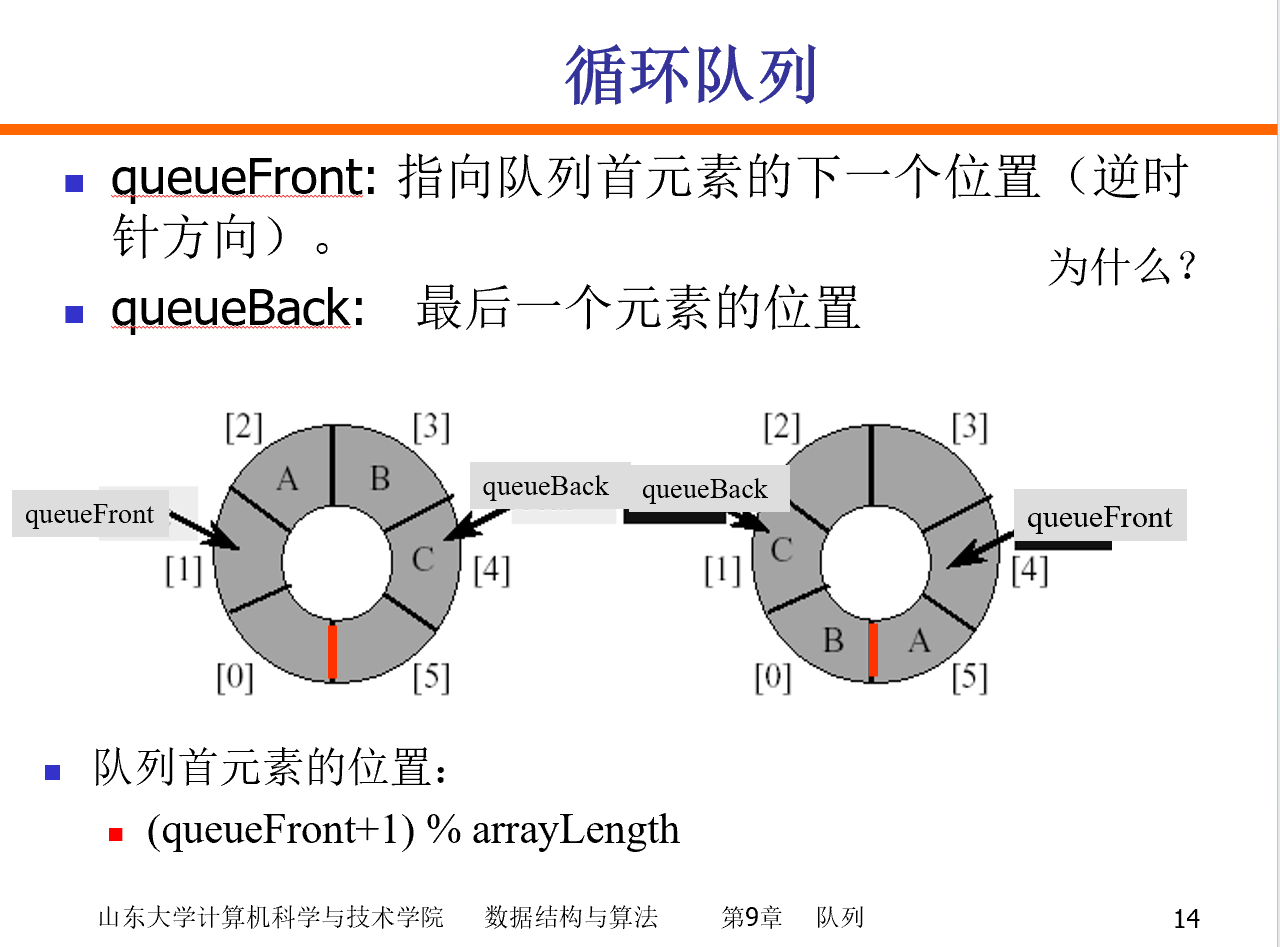
循环队列

image

七种排序（包括选择第k小）的算法思想，伪代码或者第2趟或第3趟排序结果等

image

  • 箱子排序（桶的划分规则是 “一个桶对应一个离散值”*时，桶排序就退化为箱子排序）
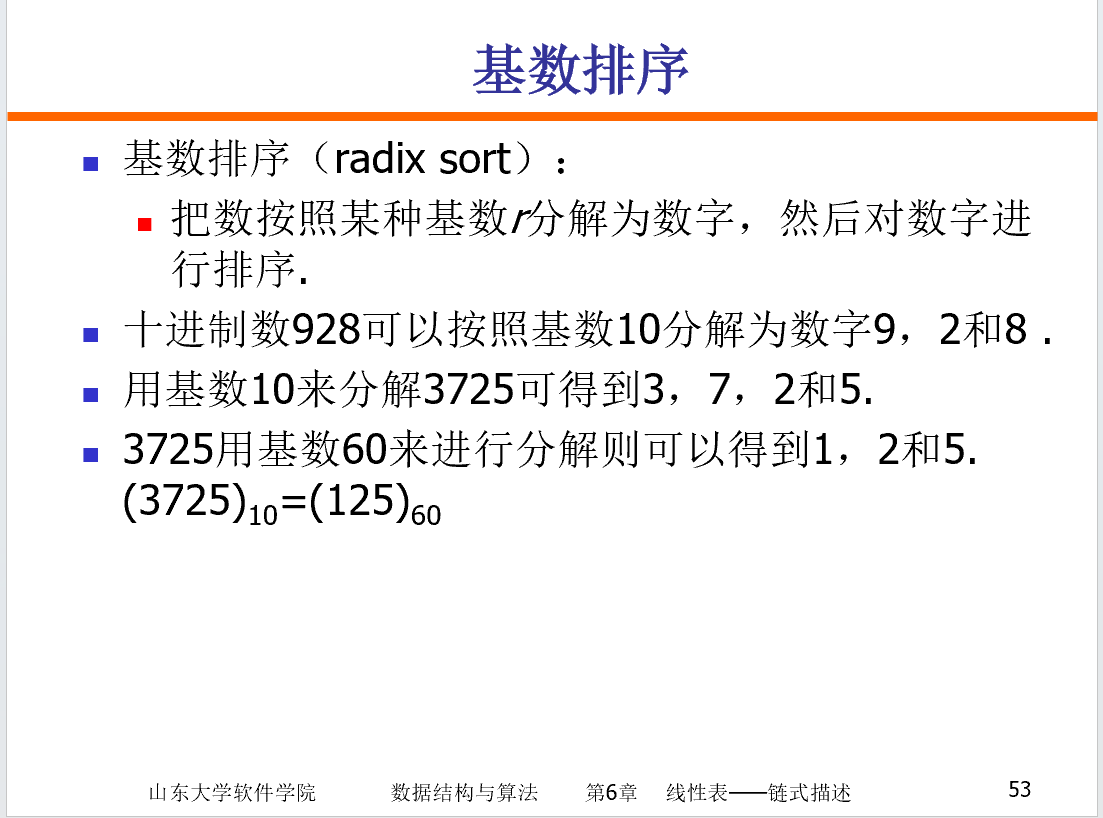
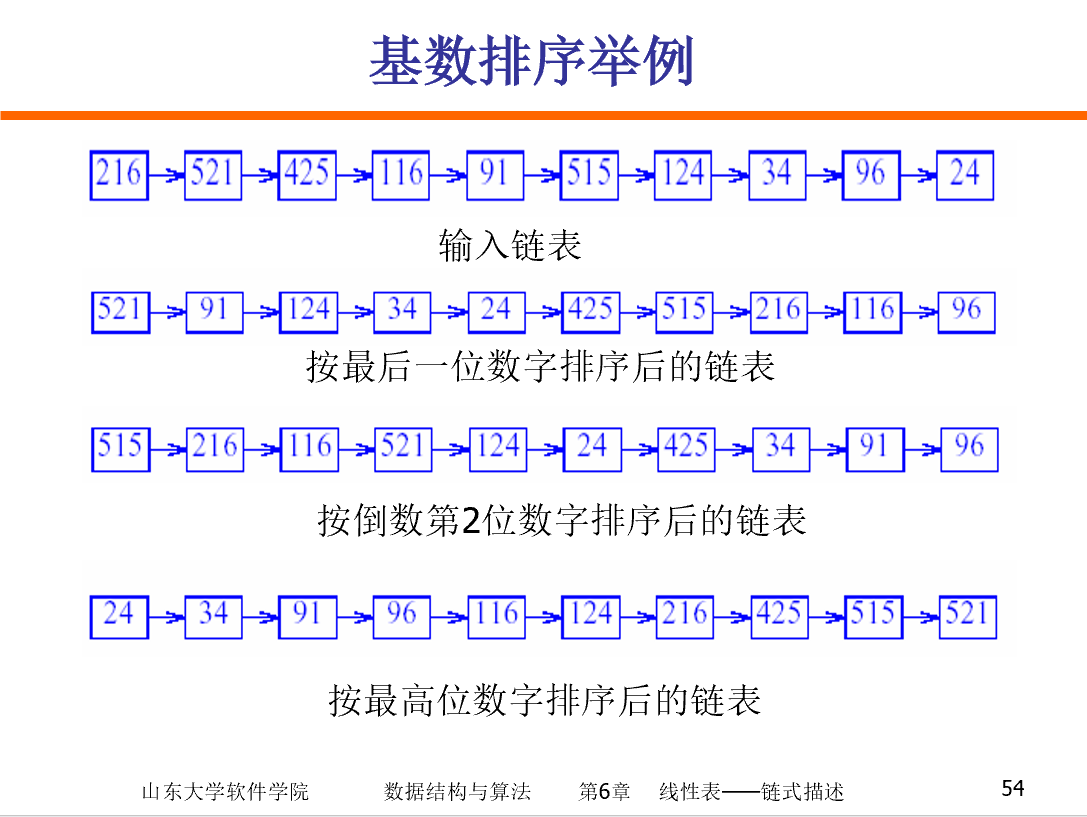
  • 基数排序
    image
    image
算法 平均时间复杂度 最坏时间复杂度 稳定性
选择排序 (Selection) O(n²) O(n²) 一般不稳定
插入排序 (Insertion) O(n²) O(n²) 稳定
冒泡排序 (Bubble) O(n²) O(n²) 稳定
归并排序 (Merge) O(n log n) O(n log n) 稳定
快速排序 (Quick) O(n log n) O(n²) 不稳定
基数排序 (Radix) O(d·(n + k)) O(d·(n + k)) 稳定（通常实现）
计数/桶/箱（离散值映射）(Counting / Bucket / Bin) O(n + k) O(n + k) 稳定（用前缀和 + 回填实现时）
堆排序 (Heap) O(n log n) O(n log n) 不稳定

选择排序

它的工作原理是每次找出第 𝑖 小的元素，然后将这个元素与数组第 𝑖 个位置上的元素交换．

  • 稳定性
    选择排序的稳定性取决于其具体实现．
    倘若使用链表实现，由于链表的任意位置插入和删除均为 𝑂(1)，故无需使用 swap（交换两个元素）操作：每次从未排序部分选择最小元素（若有多个，选取第 1 个）后，将其插入到未排序部分的第 1 个元素之前，这样就能够保证稳定性．
    假如使用数组实现（OI 中一般的实现方式），由于数组任意位置插入和删除均为 𝑂(𝑛)，故只能使用 swap 将未排序部分的元素移到已排序部分．swap 操作使得数组实现的选择排序不稳定．
点击查看代码 
void selection_sort(int* a, int n) {
  for (int i = 1; i < n; ++i) {
    int ith = i;
    for (int j = i + 1; j <= n; ++j) {
      if (a[j] < a[ith]) {
        ith = j;
      }
    }
    std::swap(a[i], a[ith]);
  }
}

冒泡排序

它的工作原理是每次检查相邻两个元素，如果前面的元素与后面的元素满足给定的排序条件，就将相邻两个元素交换．当没有相邻的元素需要交换时，排序就完成了．

  • 稳定性
    冒泡排序是一种稳定的排序算法．
点击查看代码 
// 假设数组的大小是 n + 1，冒泡排序从数组下标 1 开始
void bubble_sort(int *a, int n) {
  bool flag = true;
  while (flag) {
    flag = false;
    for (int i = 1; i < n; ++i) {
      if (a[i] > a[i + 1]) {
        flag = true;
        swap(a[i], a[i + 1]);
      }
    }
  }
}

插入排序

插入排序是一种简单直观的排序算法．它的工作原理为将待排列元素划分「已排序」和「未排序」两部分，每次从「未排序的」元素中选择一个插入到「已排序的」元素中的正确位置．
一个与插入排序相同的操作是打扑克牌时，从牌桌上抓一张牌，按牌面大小插到手牌后，再抓下一张牌．

  • 稳定性
    插入排序是一种稳定的排序算法．
点击查看代码 
void insertion_sort(int arr[], int len) {
  for (int i = 1; i < len; ++i) {
    int key = arr[i];
    int j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = key;
  }
}

计数排序

计数排序的工作原理是使用一个额外的数组 𝐶，其中第 𝑖 个元素是待排序数组 𝐴 中值等于 𝑖 的元素的个数，然后根据数组 𝐶 来将 𝐴 中的元素排到正确的位置.

  • 稳定性
    计数排序是一种稳定的排序算法．
    (此处暂保留意见)
点击查看代码 
#include <cstring>
constexpr int MAXN = 1010;
constexpr int MAXW = 100010;

int cnt[MAXW], b[MAXN];

int* counting_sort(int* a, int n, int w) {
  memset(cnt, 0, sizeof(cnt));
  for (int i = 1; i <= n; ++i) ++cnt[a[i]];
  for (int i = 1; i <= w; ++i) cnt[i] += cnt[i - 1];
  for (int i = n; i >= 1; --i) b[cnt[a[i]]--] = a[i];
  return b;
}

快速排序

快速排序的工作原理是通过 分治 的方式来将一个数组排序．
快速排序分为三个过程：

  1. 将数列划分为两部分（要求保证相对大小关系）；
  2. 递归到两个子序列中分别进行快速排序；
  3. 不用合并，因为此时数列已经完全有序．

  • 稳定性
    快速排序是一种不稳定的排序算法．

  • 非递归实现

点击查看代码 
struct Range {
  int start, end;

  Range(int s = 0, int e = 0) { start = s, end = e; }
};

template <typename T>
void quick_sort(T arr[], const int len) {
  if (len <= 0) return;
  Range r[len];
  int p = 0;
  r[p++] = Range(0, len - 1);
  while (p) {
    Range range = r[--p];
    if (range.start >= range.end) continue;
    T mid = arr[range.end];
    int left = range.start, right = range.end - 1;
    while (left < right) {
      while (arr[left] < mid && left < right) left++;
      while (arr[right] >= mid && left < right) right--;
      std::swap(arr[left], arr[right]);
    }
    if (arr[left] >= arr[range.end])
      std::swap(arr[left], arr[range.end]);
    else
      left++;
    r[p++] = Range(range.start, left - 1);
    r[p++] = Range(left + 1, range.end);
  }
}
  • 递归实现
点击查看代码 
template <typename T>
int Partition(T A[], int low, int high) {
  int pivot = A[low];
  while (low < high) {
    while (low < high && pivot <= A[high]) --high;
    A[low] = A[high];
    while (low < high && A[low] <= pivot) ++low;
    A[high] = A[low];
  }
  A[low] = pivot;
  return low;
}

template <typename T>
void QuickSort(T A[], int low, int high) {
  if (low < high) {
    int pivot = Partition(A, low, high);
    QuickSort(A, low, pivot - 1);
    QuickSort(A, pivot + 1, high);
  }
}

template <typename T>
void QuickSort(T A[], int len) {
  QuickSort(A, 0, len - 1);
}
  • 优化：三路式快排
点击查看代码 
// 模板的 T 参数表示元素的类型，此类型需要定义小于（<）运算
template <typename T>
// arr 为需要被排序的数组，len 为数组长度
void quick_sort(T arr[], const int len) {
  if (len <= 1) return;
  // 随机选择基准（pivot）
  const T pivot = arr[rand() % len];
  // i：当前操作的元素下标
  // arr[0, j)：存储小于 pivot 的元素
  // arr[k, len)：存储大于 pivot 的元素
  int i = 0, j = 0, k = len;
  // 完成一趟三路快排，将序列分为：
  // 小于 pivot 的元素 | 等于 pivot 的元素 | 大于 pivot 的元素
  while (i < k) {
    if (arr[i] < pivot)
      swap(arr[i++], arr[j++]);
    else if (pivot < arr[i])
      swap(arr[i], arr[--k]);
    else
      i++;
  }
  // 递归完成对于两个子序列的快速排序
  quick_sort(arr, j);
  quick_sort(arr + k, len - k);
}

归并排序

归并排序最核心的部分是合并（merge）过程：将两个有序的数组 a[i] 和 b[j] 合并为一个有序数组 c[k]。
从左往右枚举 a[i] 和 b[j]，找出最小的值并放入数组 c[k]；重复上述过程直到 a[i] 和 b[j] 有一个为空时，将另一个数组剩下的元素放入 c[k]。
为保证排序的稳定性，前段首元素小于或等于后段首元素时（a[i] <= b[j]）而非小于时（a[i] < b[j]）就要作为最小值放入 c[k]。

  • 数组实现
点击查看代码 
void merge(const int *a, size_t aLen, const int *b, size_t bLen, int *c) {
  size_t i = 0, j = 0, k = 0;
  while (i < aLen && j < bLen) {
    if (b[j] < a[i]) {  // <!> 先判断 b[j] < a[i]，保证稳定性
      c[k] = b[j];
      ++j;
    } else {
      c[k] = a[i];
      ++i;
    }
    ++k;
  }
  // 此时一个数组已空，另一个数组非空，将非空的数组并入 c 中
  for (; i < aLen; ++i, ++k) c[k] = a[i];
  for (; j < bLen; ++j, ++k) c[k] = b[j];
}
  • 指针实现
点击查看代码 
void merge(const int *aBegin, const int *aEnd, const int *bBegin,
           const int *bEnd, int *c) {
  while (aBegin != aEnd && bBegin != bEnd) {
    if (*bBegin < *aBegin) {
      *c = *bBegin;
      ++bBegin;
    } else {
      *c = *aBegin;
      ++aBegin;
    }
    ++c;
  }
  for (; aBegin != aEnd; ++aBegin, ++c) *c = *aBegin;
  for (; bBegin != bEnd; ++bBegin, ++c) *c = *bBegin;
}

基数排序

基数排序是一种非比较型的排序算法，最早用于解决卡片排序的问题．基数排序将待排序的元素拆分为 𝑘 个关键字，逐一对各个关键字排序后完成对所有元素的排序．

第十章 跳表和散列

·给出哈希函数和探测方式（链表方式），哈希存储过程和查找一个元素时需要的比较次数

散列表：

多维护一个 used 数组，初始为0.

    1. 插入
      算哈希函数，冲突就往后找
      遇到空格就插，不管 used 状态（used=1但是是空的就说明曾经删掉过数）
    1. 查找
      从哈希位置开始逐个找
      找到目标就 return
      遇到空格且 used == 0 就失败
    1. 删除
      从哈希位置开始逐个找
      找到就删，注意 used 状态不再重置

散列表：

多维护一个 used 数组，初始为0.

第十一章 树

·二叉树三种遍历序列，给两个求另一个，或者给两个画出树过程思想和伪代码
·二叉树中统计叶子节点个数，度为1或者2的节点个数，树的高度等算法思想

二叉树的性质

  • 树的边数一定为 \(n-1\).
    证明：除了根节点每个节点有且仅有一个父节点
    而父子节点之间有且仅有一条边
    证毕.

  • 高度为 \(h\) 的二叉树节点个数 \(h \le x \le 2 ^ h - 1\)
    左等号取等，退化为链表；右等号取等，满二叉树。

  • 节点个数为 \(n\) 的二叉树高度范围 \(\left\lceil\log_2 (n+1)\right\rceil \le h \le n\)

  • 完全二叉树
    前k-1层是满二叉树，最后一层的节点全在左边（层序遍历连续）

  • 前中后层序遍历

第十二章 优先队列

·最大最小堆的初始化，堆排序，堆删除元素等调节过程
·霍夫曼树的构建和编码
区分大根树和大根堆

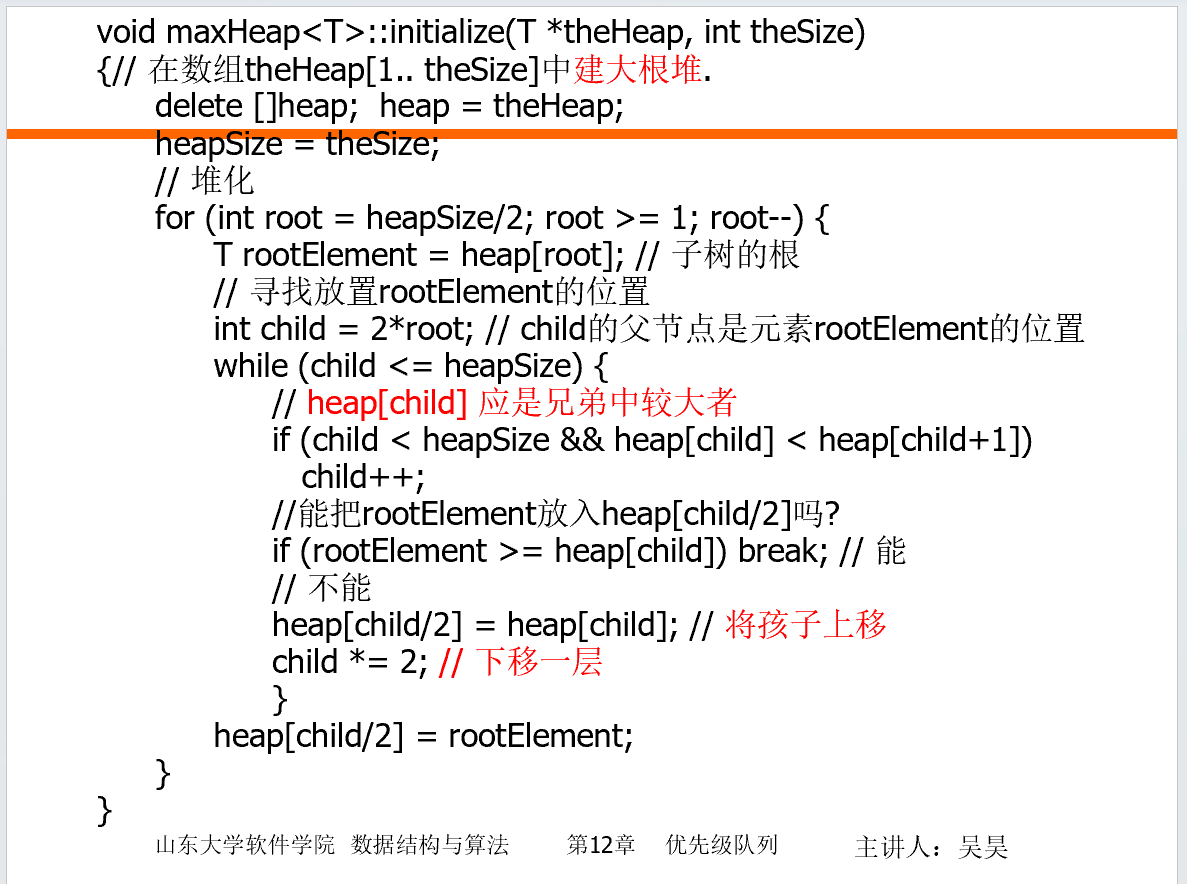
堆的初始化

从第一个不是叶子节点的最大节点（floor(n/2)）开始，每个做一次自顶向下修复。复杂度 O(n).
image

霍夫曼算法

  1. 初始化：由给定的 ( n ) 个权值构造 ( n ) 棵只有一个根节点的二叉树，得到一个二叉树集合 ( F )。
  2. 选取与合并：从二叉树集合 ( F ) 中选取根节点权值 最小的两棵 二叉树分别作为左右子树构造一棵新的二叉树，这棵新二叉树的根节点的权值为其左、右子树根结点的权值和。
  3. 删除与加入：从 ( F ) 中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到 ( F ) 中。
  4. 重复步骤：重复 2、3 步，当集合中只剩下一棵二叉树时，这棵二叉树就是霍夫曼树。

可以用于构造霍夫曼编码，解决构造带权路径长度最小的树的构造问题。

左高树（重量优先， 高度优先）

第十四章 搜索树

  • 二叉搜索树
    image
  • 索引二叉搜索树
    在二叉搜索树的基础上，在每个节点中添加一个“LeftSize”表示该节点左子树节点个数
    于是 LeftSize(x) 给出了一个节点在 x 为根的子树中的排名（从0开始）
    增删改查 ？

第十五章 平衡搜索树

·AVL搜索树的插入导致失衡的四种情况LL LR RR和RL、删除一个节点的六种情况R0，R1，R-1，L0，L1，L-1，以及他们调整过程。
·m阶B树的插入和删除操作，插入时注意饱和的情况，饱和时需要拆分，删除时注意节点中元素的个数少于m/2的上界时，需要合并节点

AVL 树

image
其中AVL搜索树（平衡二叉搜索树），既是二叉搜索树，也是AVL树。

平衡因子：节点的左子树高度 - 节点的右子树高度
于是可能取值为 \(-1，0，1\)

发生失衡

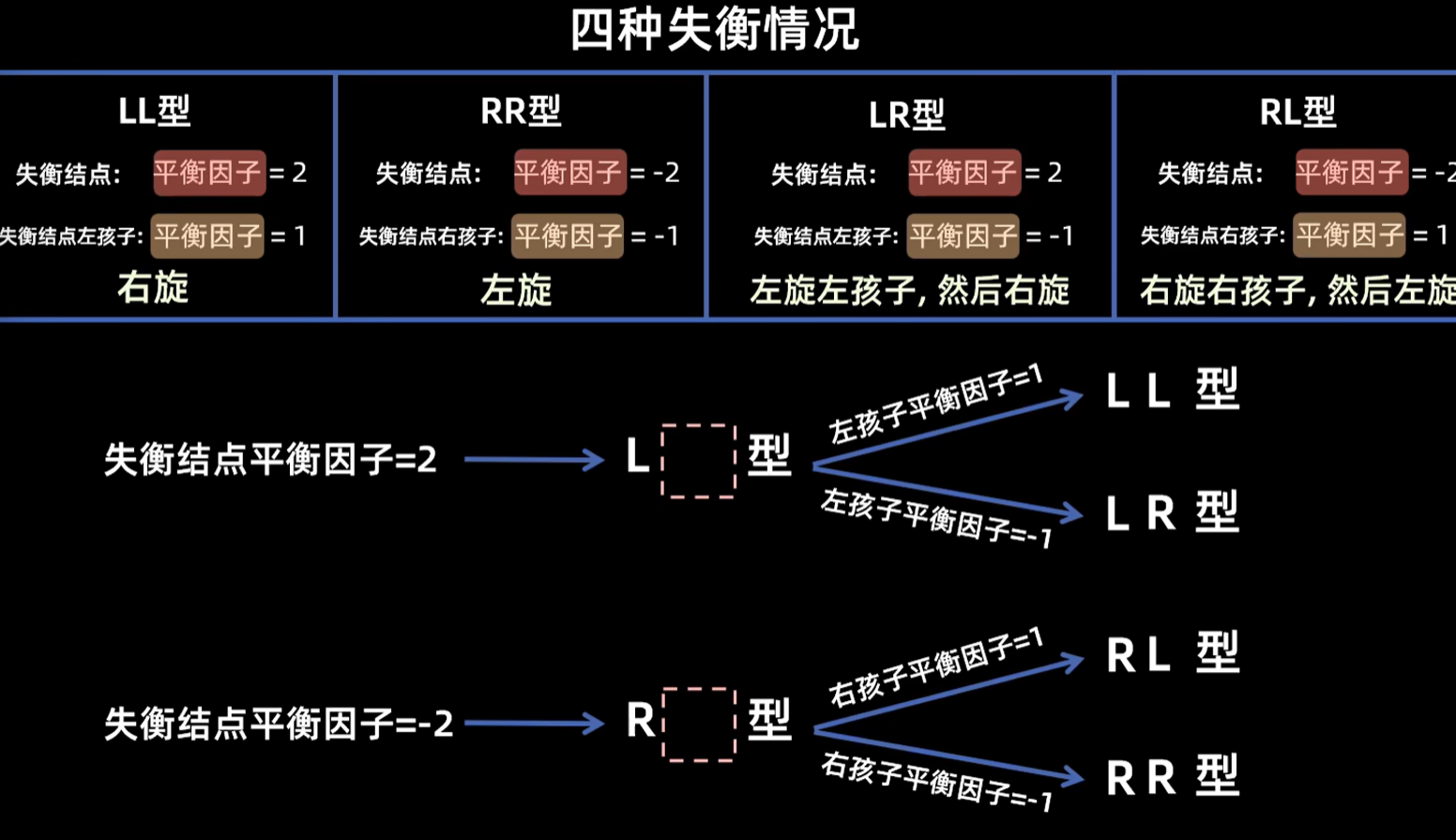
image

修复失衡

左旋：向左旋转，冲突的左孩子变成右孩子
右旋：向右旋转，冲突的右孩子变成左孩子

  • LL型：插入的新节点在左孩子的右子树上
    特征：失衡节点的平衡因子是 \(2\)，失衡节点的左孩子的平衡因子是 \(1\).
    调整：右旋

注意插入导致的失衡只需要修最近那个

B-树

B+树

第十六章 图

·拓扑排序
·图是否为连通图，图的连通构件，有向图是否存在环路等算法思想和伪代码
·Kruskal，Prim最小耗费生成树，Dijkstra，Floyd单源和多源最短路径算法的思想，计算过程，满足的特征等
存图方法：邻接矩阵、邻接链表、邻接数组

第十七章 贪心

背包问题

最短路

最小生成树

第十八章 分治

快排、归并、选择

第十九章 DP

·动态规划，贪心算法，给一个问题，用这两个思想进行分析，算法思想，伪代码，时间复杂度分析等
·结合离散数学中的一些动态规划算法，比如爬台阶问题

Floyd

posted @ 2026-01-11 17:33  [丘李]Chilllee  阅读(1)  评论(0)    收藏  举报