模板索引：图论
搜索
深度优先搜索DFS
- 回溯算法的一般形式如下:
void dfs(int k) { // k 代表递归层数,或者说要填第几个空
if ( 所有空已经填完了 ) {
判断最优解 / 记录答案 ;
return;
}
for ( 枚举这个空能填的选项 )
if ( 这个选项是合法的 ) {
记录下这个空 (保存现场);
dfs(k + 1);
取消这个空 (恢复现场);
}
- 例如：八皇后问题
void dfs(int x){
if(x > n){
ans++;
if(ans <= 3){
for(int i=1; i<=n; i++) printf("%d ", a[i]);
printf("\n");
}
return ;
}
for(int i=1; i<=n; i++){
if(!b[i] && !xie1[x+i] && !xie2[x-i+15]){
a[x] = i;
b[i] = xie1[x + i] = xie2[x - i + 15] = 1;
dfs(x+1);
b[i] = xie1[x + i] = xie2[x - i + 15] = 0;
}
}
}
广度优先搜索算法
- 广度优先搜索的一般形式如下:
Q.push(初始状态); // 将初始状态入队
while (!Q.empty()) {
State u = Q.front(); // 取出队首
Q.pop(); // 出队
for (枚举所有可扩展状态) // 找到 u 的所有可达状态 v
if (是合法的) // v 需要满足某些条件,如未访问过、未在队内等
Q.push(v); // 入队 (同时可能需要维护某些必要信息)
}
- 例如：马的遍历(洛谷 P1443)。有一个\(n\times m\)的棋盘(1<n,m<400),在某个点上有一个马，要求计算出马到达棋盘上任意一个点最少要走几步。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 310;
struct node{
int x;
int y;
};
queue<node> q;
int ans[maxn][maxn];
int to[8][2] = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}};
int main(){
int n, m, startx, starty;
memset(ans, -1, sizeof(ans));
cin >> n >> m >> startx >> starty;
node tmp = {startx, starty};
q.push(tmp);
ans[startx][starty] = 0;
while(!q.empty()){
node now = q.front();
int nowx = now.x, nowy = now.y;
q.pop();
for(int k=0; k < 8; k++){
int x = nowx + to[k][0], y = nowy + to[k][1];
int step = ans[nowx][nowy];
if(x < 1 || x > n || y < 1 || y > m || ans[x][y] != -1) continue;
ans[x][y] = step + 1;
node tmp = {x, y};
q.push(tmp);
}
}
for(int i = 1;i <= n; i++,puts(""))
for(int j = 1;j <= m; j++)
printf("%-5d", ans[i][j]); //场宽输出
return 0;
}
图的存储问题
带权图存储
- 邻接矩阵：只需要用w[u][v]从存0/1改成存边权即可。
- vector：需要写个struct，来把「邻居编号」和「边权」打包起来。
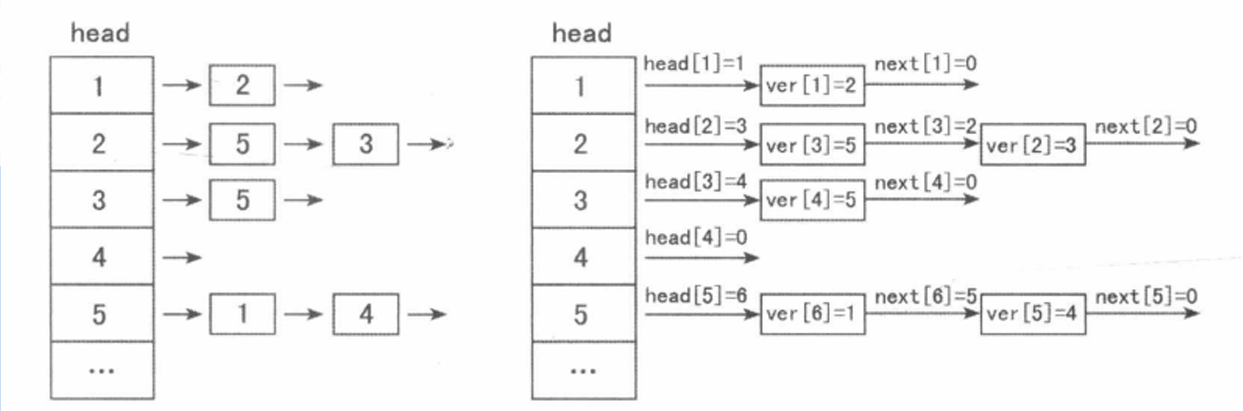
链式前向星
对于无向图，只需要将 M 的大小 ×2，再将反向边也插入链式前向星中即可。
vector 无法快速查找一条边的反向边。在链式前向星中，如果我们初始化 k=1，那么每条无向边看成的两条有向边会成对存储在数组下标 2/3,4/5,6/7… 的位置上。对于一条下标为 i 的边，可以通过 i xor 1 快速得到其反向边的下标
int h[maxn], to[maxm], nxt[maxm], cnt;
inline void add(int u, int v){
to[++cnt] = v;
nxt[cnt] = h[u];
h[u] = cnt;
}
拓扑排序技术
示例：
int n, m;
vector<int> G[MAXN];
int in[MAXN]; // 存储每个结点的入度
bool toposort() {
vector<int> L;
queue<int> S;
for (int i = 1; i <= n; i++)
if (in[i] == 0) S.push(i);
while (!S.empty()) {
int u = S.front();
S.pop();
L.push_back(u);
for (auto v : G[u]) {
if (--in[v] == 0) {
S.push(v);
}
}
}
if (L.size() == n) {
for (auto i : L) cout << i << ' ';
return true;
}
return false;
}
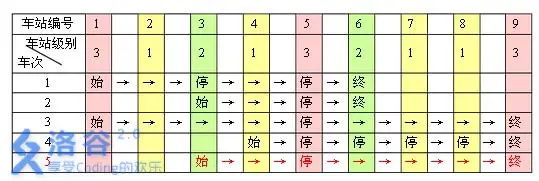
一条单向的铁路线上，依次有编号为 \(1, 2, …, n\) 的 $n $ 个火车站。每个火车站都有一个级别，最低为 \(1\) 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 \(x\)，则始发站、终点站之间所有级别大于等于火车站 \(x\) 的都必须停靠。
注意：起始站和终点站自然也算作事先已知需要停靠的站点。
例如，下表是 $ 5 $ 趟车次的运行情况。其中，前 $ 4$ 趟车次均满足要求，而第 \(5\) 趟车次由于停靠了 \(3\) 号火车站（\(2\) 级）却未停靠途经的 \(6\) 号火车站（亦为 \(2\) 级）而不满足要求。
现有 \(m\) 趟车次的运行情况（全部满足要求），试推算这 $ n$ 个火车站至少分为几个不同的级别。
- 优化建图，拓扑排序
- 注意这个可以用队列优化到O(n+m)
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1010;
int n, m;
vector<int> g[maxn];
int in[maxn], vis[maxn];
bitset<maxn> hasEdge[maxn];
// bitset防止边重复，否则会MLE，也可以用二维bool数组，效果是一样的
void adde(int u, int v){
if(!hasEdge[u].test(v)){
hasEdge[u].set(v);
g[u].push_back(v);
in[v]++;
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x;
cin >> x;
vector<int> vc(x);
for(int j = 0; j < x; j++) cin >> vc[j];
int fl = 0;
vector<int> small;
for(int j = vc[0]; j < vc[x-1]; j++){
if(j == vc[fl]) fl++;
else small.push_back(j);
}
for(auto ita : vc)
for(auto itb : small)
adde(ita, itb);
}
int cnt = 0, ans = 0;
while(cnt < n){
vector<int> cur;
for(int i = 1; i <= n; i++){
if(!vis[i] && in[i] == 0) cur.push_back(i);
}
// 特别注意前面的点如果先删除，可能后面原本在次一层的点就会暴露出来，所以先统计在删边
if(cur.empty()) break;
ans++;
for(int u : cur){
vis[u] = 1;
cnt++;
}
for(int u : cur){
for(auto v : g[u]) in[v]--;
}
}
cout << ans << '\n';
return 0;
}
最短路问题
单源最短路算法
- 朴素做法 \(O(n ^ 2)\)
伪代码：
点击查看代码
struct edge {
int v, w;
};
vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
void dijkstra(int n, int s) {
memset(dis, 0x3f, (n + 1) * sizeof(int));
dis[s] = 0;
for (int i = 1; i <= n; i++) {
int u = 0, mind = 0x3f3f3f3f;
for (int j = 1; j <= n; j++)
if (!vis[j] && dis[j] < mind) u = j, mind = dis[j];
vis[u] = true;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) dis[v] = dis[u] + w;
}
}
}
- 堆优化做法 \(O(mlogm)\)
- 注意如果 \(m\) 与 \(n ^2\) 同级，即稠密甚至完全图，那么复杂度 O(n ^ 2 log (n ^ 2))）劣于朴素算法
伪代码：
点击查看代码
struct edge {
int v, w;
};
struct node {
int dis, u;
bool operator>(const node& a) const { return dis > a.dis; }
};
vector<edge> e[MAXN];
int dis[MAXN], vis[MAXN];
priority_queue<node, vector<node>, greater<node>> q;
void dijkstra(int n, int s) {
memset(dis, 0x3f, (n + 1) * sizeof(int));
memset(vis, 0, (n + 1) * sizeof(int));
dis[s] = 0;
q.push({0, s});
while (!q.empty()) {
int u = q.top().u;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto ed : e[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
}
- 0-1 bfs伪代码：
点击查看代码
while (队列不为空) {
int u = 队首;
弹出队首;
for (枚举 u 的邻居) {
更新数据
if (...)
添加到队首;
else
添加到队尾;
}
}
多源最短路算法
伪代码：
点击查看代码
for (k = 1; k <= n; k++) {
for (x = 1; x <= n; x++) {
for (y = 1; y <= n; y++) {
f[x][y] = min(f[x][y], f[x][k] + f[k][y]);
}
}
}
分层图问题
Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务，设这些城市分别标记为 \(0\) 到 \(n-1\)，一共有 \(m\) 种航线，每种航线连接两个城市，并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, m, s, cnt;
int k, t;
const int inf = 0x7fffffff;
const int maxn = 4e6+10;
int dis[maxn], h[maxn], to[maxn], val[maxn], nxt[maxn];
bool vis[maxn];
struct node {
int v,w;
friend bool operator < (node a,node b){
return a.w > b.w;
}
}tmp;
priority_queue<node>q;
void add(int u,int v,int w){
to[++cnt]= v;
val[cnt]= w;
nxt[cnt]= h[u];
h[u]= cnt;
}
void dijkstra(){
memset(dis,0x3f,sizeof(dis));
dis[s]= 0;
tmp.v = s, tmp.w = 0;
q.push(tmp);
while(!q.empty()){
int u= q.top().v;
q.pop();
if(vis[u]) continue;
vis[u] = 1;
for(int i= h[u]; i; i = nxt[i]){
if(dis[to[i]] > (long long)dis[u] + val[i])
dis[to[i]] = dis[u] + val[i];
tmp.w = dis[to[i]], tmp.v = to[i]; q.push(tmp);
}
}
}
int main(){
cin>>n>>m>>k;
cin>>s>>t;
for(int i=1; i<=m; i++){
int u= read();
int v= read();
int w= read();
add(u, v, w);
add(v, u, w);
for(int j=1; j<=k; j++) {
add(u + j*n - n, v + j*n, 0);
add(v + j*n - n, u + j*n, 0);
add(u + j*n, v + j*n, w);
add(v + j*n, u + j*n, w);
}
}
dijkstra();
int ans = inf;
for(int i=1;i<=k;++i)
{
add(t+(i-1)*n,t+i*n,0);
}
for(int j=0; j<=k; j++)
if(dis[t+j*n] < ans )
ans= dis[t + j*n];
cout<<ans<<endl;
return 0;
}
P7297 [USACO21JAN] Telephone G
Farmer John 的 N 头奶牛，编号为 \(1…N\)，站成一行（\(1≤N≤5⋅10^4\)）。第 \(i\) 头奶牛的品种编号为 \(b_i\)，范围为 \(1\dots K\)，其中 \(1≤K≤50\)。奶牛们需要你帮助求出如何最优地从奶牛 \(1\) 传输一条信息到奶牛 \(N\)。
从奶牛 \(i\) 传输信息到奶牛 \(j\) 花费时间 \(|i-j|\)。然而，不是所有品种的奶牛都愿意互相交谈，如一个 \(K\times K\) 的方阵 \(S\) 所表示，其中如果一头品种 \(i\) 的奶牛愿意传输一条信息给一头品种 \(j\) 的奶牛，那么 \(S_{ij}=1\)，否则为 \(0\)。不保证 \(S_{ij}=S_{ji}\)，并且如果品种 \(i\) 的奶牛之间不愿意互相交流时可以有 \(S_{ii}=0\)。
请求出传输信息所需的最小时间。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pr; // 题解1讲的真的很好
#define mk make_pair
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
int n, k;
int b[maxn];
char s[55][55];
int dis[maxn * 50];
int vis[maxn * 50];
vector<pr> g[maxn * 50];
void adde(int u, int v, int w = 0, int f = 0){
g[u].push_back(mk(v, w));
if(f) g[v].push_back(mk(u, w));
}
struct node{
int w, u;
friend bool operator < (node x, node y){
return x.w > y.w;
}
};
priority_queue<node> qu;
void dijk(){
//for(int i = 1; i <= n; i++) dis[i] = inf;
memset(dis, 0x3f, sizeof(dis));
dis[1] = 0;
node tmp = {0, 1};
qu.push(tmp);
while(!qu.empty()){
int u = qu.top().u;
qu.pop();
if(vis[u]) continue;
vis[u] = 1;
for(auto it : g[u]){
int v = it.first, w = it.second;
if(dis[v] > (ll) dis[u] + w)
dis[v] = dis[u] + w;
tmp = {dis[v], v};
qu.push(tmp);
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> b[i];
for(int i = 1; i <= k; i++){
cin >> s[i] + 1;
}
// 除了第0层之外，建立连边
for(int j = 1; j <= k; j++)
for(int i = 1; i <= n - 1; i++) adde(i + j * n, i + 1 + j * n, 1, 1);
// 建立第0层到对应颜色层的单向边
for(int i = 1; i <= n; i++) adde(i, b[i] * n + i);
// 如果可以从某种颜色到这个点的本色，就连单向边
for(int j = 1; j <= n; j++)
for(int i = 1; i <= k; i++)
if(s[i][b[j]] == '1') adde(i * n + j, j);
// 注意不能在每一层取min来输出ans，因为要有对应的传递关系才有1-k层到第0层的回边
dijk();
if(dis[n] == inf) cout << -1 << endl;
else cout << dis[n] << endl;
return 0;
}
传递闭包
- 思路类似Floyd
- bitset压位处理
P4306 [JSOI2010] 连通数
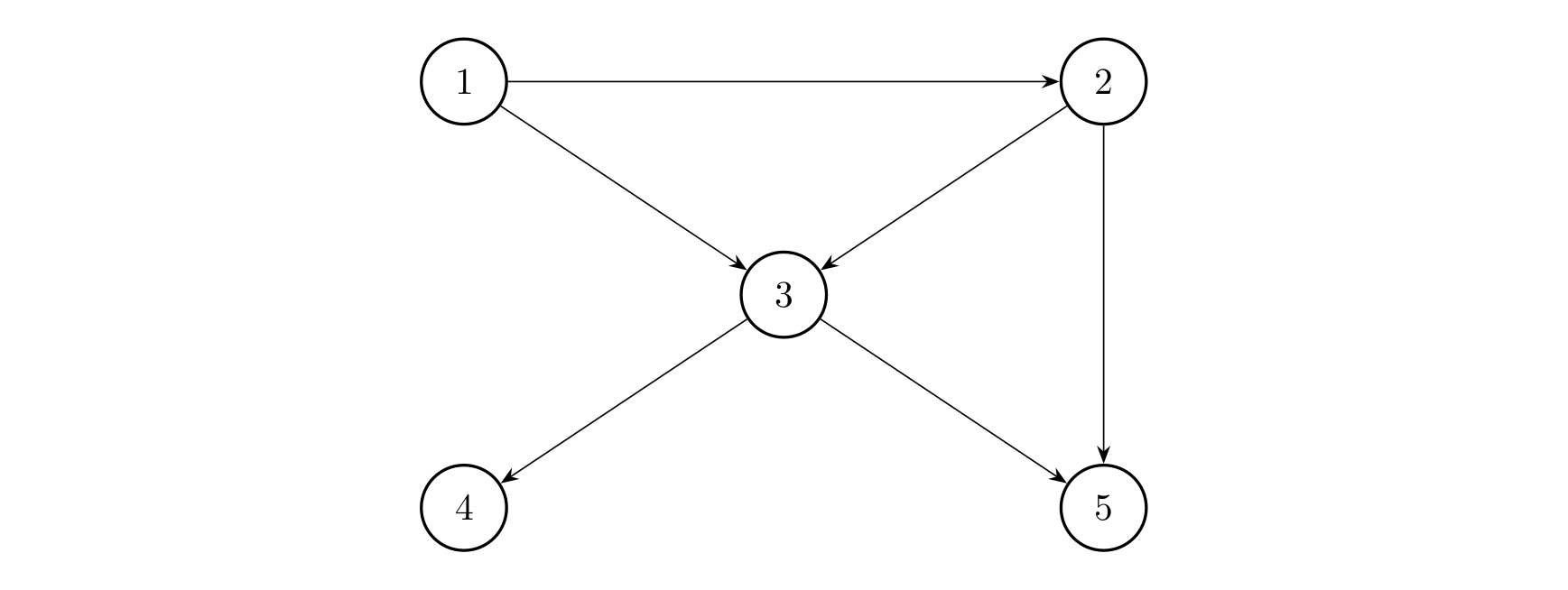
度量一个有向图连通情况的一个指标是连通数，指图中可达顶点对个的个数。
如图
顶点 \(1\) 可达 \(1, 2, 3, 4, 5\)
顶点 \(2\) 可达 \(2, 3, 4, 5\)
顶点 \(3\) 可达 \(3, 4, 5\)
顶点 \(4, 5\) 都只能到达自身。
所以这张图的连通数为 \(14\)。
给定一张图，请你求出它的连通数
对于 \(100 \%\) 的数据，\(1 \le N \le 2000\)。
bitset优化
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2020;
int n;
bitset<maxn> b[maxn];
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n;
for(int i = 1; i <= n; i++){
string s;
cin >> s; // 不要用 scanf(" %s", string); 这是未定义行为，有极大的副作用。scanf %s 最好只用于char数组
s = "0" + s;
for(int j = 1; j <= n; j++)
if(i == j) b[i][j] = 1;
else b[i][j] = s[j] - '0';
}
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
if(b[i][k]){
/*
下面的 1 就是 b[i][k]，提取出来判断了
for(int j = 1; j <= n; j++)
b[i][j] = b[i][j] | (1 & b[k][j]);
继续优化为；
for(int j = 1; j <= n; j++)
b[i][j] = b[i][j] | b[k][j];
于是最终优化为：
*/
b[i] = b[i] | b[k];
}
int ans = 0;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
ans += b[i][j];
cout << ans << endl;
return 0;
}
优化建图
- 完全图最短路问题
P4366 [Code+#4] 最短路
企鹅国中有 \(N\) 座城市，编号从 \(1\) 到 \(N\)。
对于任意的两座城市 \(i\) 和 \(j\)，企鹅们可以花费 \((i~\mathrm{xor}~j) \times C\) 的时间从城市 \(i\) 走到城市 \(j\)，这里 \(C\) 为一个给定的常数。
当然除此之外还有 \(M\) 条单向的快捷通道，第 \(i\) 条快捷通道从第 \(F_i\) 个城市通向第 \(T_i\) 个城市，走这条通道需要消耗 \(V_i\) 的时间。
考虑从城市 \(A\) 前往城市 \(B\) 最少需要多少时间？
- 优化建图题由于边数极大，大概率不会给你边，而是给你算法你自己生成出来。我们当然也不能自己全部建完。
- 可以证明，对于一个点
u，连接u ^ 1,u ^ 2,u ^ 4...u ^ (2 ^ j)的边，可以替代表示所有所需的边。无论连通性还是边权消耗都与原来一样。 - 于是现在边的数量只有 \(O(nlog)\) 了，完全可跑。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pr;
#define mk make_pair
const int maxn = 1e5 + 10;
// 优化建图
int n, m, c;
int st, ed;
int dis[maxn];
int vis[maxn];
vector<pr> g[maxn];
void adde(int u, int v, int w){
g[u].push_back(mk(v, w));
}
struct node{
int u;
int w;
friend bool operator < (node x, node y){
return x.w > y.w;
}
};
priority_queue<node> qu;
void dijk(){
dis[st] = 0;
node tmp = {st, 0}; // 一定要注意定义的顺序
qu.push(tmp);
while(!qu.empty()){
int u = qu.top().u;
qu.pop();
if(vis[u]) continue;
vis[u] = 1;
for(auto it : g[u]){
int v = it.first, w = it.second;
if(dis[v] > (long long) dis[u] + w){
dis[v] = dis[u] + w;
tmp = {v, dis[v]};
qu.push(tmp);
}
}
for(int j = 1; j <= n * 2; j <<= 1) // !!!
if((u ^ j) <= n && (ll) dis[u] + j * c < dis[u ^ j]){ // !!! 一定要注意写法，是判断终点在不在n的范围内
dis[u ^ j] = dis[u] + j * c;
qu.push({u ^ j, dis[u ^ j]});
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> c;
for(int i = 1; i <= m; i++){
int u, v, w;
cin >> u >> v >> w;
adde(u, v, w);
}
cin >> st >> ed;
memset(dis, 0x3f, sizeof(dis));
dijk();
cout << dis[ed] << endl;
return 0;
}
P1948 [USACO08JAN] Telephone Lines S
多年以后，笨笨长大了，成为了电话线布置师。由于地震使得某市的电话线全部损坏，笨笨是负责接到震中市的负责人。该市周围分布着 \(n\)（\(1\le n\le10^3\)）根按 \(1\sim n\) 顺序编号的废弃的电话线杆，任意两根线杆之间没有电话线连接，一共有 \(p\)（\(1\le p\le10^4\)）对电话杆可以拉电话线。其他的由于地震使得无法连接。
第 \(i\) 对电线杆的两个端点分别是 \(a_i,b_i\)，它们的距离为 \(l_i\)（\(1\le l_i\le10^6\)）。数据中每对 \((a_i,b_i)\) 只出现一次。编号为 \(1\) 的电话杆已经接入了全国的电话网络，整个市的电话线全都连到了编号 \(n\) 的电话线杆上。也就是说，笨笨的任务仅仅是找一条将 \(1\) 号和 \(n\) 号电线杆连起来的路径，其余的电话杆并不一定要连入电话网络。
电信公司决定支援灾区免费为此市连接 \(k\) （\(1\le k\le p\)）对由笨笨指定的电话线杆，对于额外的那些电话线，需要为它们付费，总费用决定于其中最长的电话线的长度（每根电话线仅连接一对电话线杆）。如果需要连接的电话线杆不超过 \(k\) 对，那么支出为 \(0\)。
请你计算一下，将电话线引导震中市最少需要在电话线上花多少钱？
- 考虑最小化最大问题，显然优先考虑二分答案x
- 验证思路用 dijk，但是如果每次都根据这条边是不是大于 x 来建图，每次建个图非常麻烦
于是可以直接判断这条边是不是大于 x，如果大于，那么就要消耗一次免费次数，dis++。
而如果小于等于 x，可以认为这条边免费。 - 由于边只有 0，1 两种状态，这题可以使用 0-1 bfs 进一步优化。
这题可以用堆优化disjk，也可以用 0-1 bfs（代码如下）。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pr; // 0-1bfs, 优化建图
#define mk make_pair
const int maxn = 1e3 + 10;
int n, p, k;
int dis[maxn], vis[maxn];
vector<pr> g[maxn];
void adde(int u, int v, int w){
g[u].push_back(mk(v, w));
}
bool check(int x){
memset(dis, 0x3f, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[1] = 0;
deque<int> qu;
qu.push_back(1);
while(!qu.empty()){
int u = qu[0];
qu.pop_front();
if(vis[u]) continue;
vis[u] = 1;
for(auto it : g[u]){
int v = it.first, w = it.second;
int e = w > x;
if(dis[v] > (ll) dis[u] + e){
dis[v] = dis[u] + e;
if(!e) qu.push_front(v);
else qu.push_back(v);
}
}
}
return dis[n] <= k;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> p >> k;
for(int i = 1; i <= p; i++){
int u, v, w;
cin >> u >> v >> w;
adde(u, v, w);
adde(v, u, w);
}
int l = 0, r = 1e9, ans = -1;
while(l <= r){
int mid = (l + r) >> 1;
if(check(mid)){
ans = mid;
r = mid - 1;
}
else l = mid + 1;
}cout << ans << endl;
return 0;
}
P6348 [PA 2011] Journeys
连通性问题
强连通分量SCC
例题 洛谷P3387【模板】缩点
给定一个n 个点m 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e4 + 10;
const int maxm = 1e5 + 10;
vector<int> mp[maxn], G[maxn]; // 原图；缩点后的DAG
int n, m;
int A[maxn]; // 点权
int dfn[maxn], low[maxn], T; // dfs序；经过不超过一条非树边能到达的最浅节点；dfn的cnt：T
int stk[maxn], top; // 维护一个未被分配进SCC的栈
bool ins[maxn];// 某个点是否在上一行的栈里
int S[maxn], SCC; // 维护某个点在哪个SCC里，以及计数
int sum[maxn]; // 每一个SCC的点权和；
int f[maxn], in[maxn]; // 拓扑排序；in是入度
void dfs(int u){
dfn[u] = low[u] = ++T;
stk[++top] = u;
ins[u] = 1;
for(auto v : mp[u]){
if(dfn[v] == 0){
dfs(v);
low[u] = min(low[u], low[v]);
}
else if(ins[v]) low[u] = min(low[u], dfn[v]);
}
if(dfn[u] == low[u]){
++SCC;
while(stk[top] != u){
int p = stk[top--];
ins[p] = 0;
S[p] = SCC;
sum[SCC] += A[p];
}
ins[u] = 0;
S[u] = SCC;
sum[SCC] += A[u];
--top;
}
}
queue<int> q;
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> A[i];
for(int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
mp[u].push_back(v);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) dfs(i); // 注意可能有多个非连通图
for(int i = 1; i <= n; i++)
for(auto v : mp[i])
if(S[i] != S[v]) G[S[i]].push_back(S[v]), in[S[v]]++; // 统计入度
for(int i = 1; i <= SCC; i++)
if(!in[i]) q.push(i), f[i] = sum[i];
while(!q.empty()){
int u = q.front();
q.pop();
for(auto v : G[u]){
f[v] = max(f[v], f[u] + sum[v]);
--in[v];
if(!in[v]) q.push(v);
}
}
int ans = 0;
for(int i = 1; i <= SCC; i++)
ans = max(ans, f[i]);
cout << ans << endl;
return 0;
}
例题 P2863 [USACO06JAN] The Cow Prom S
有一个 \(n\) 个点，\(m\) 条边的有向图，请求出这个图点数大于 \(1\) 的强连通分量个数。
// 进阶篇
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 10;
const int maxm = 5e4 + 10;
int n, m;
int head[maxn], nxt[maxn], to[maxn], tot;
void adde(int u, int v){
nxt[++tot] = head[u]; to[head[u] = tot] = v;
}
int dfn[maxn], low[maxn], T;
int stk[maxn], top;
bool ins[maxn];
int SCC[maxn], scc, siz[maxn];
void dfs(int u){
dfn[u] = low[u] = ++T;
ins[stk[++top] = u] = 1;
for(int i = head[u]; i; i = nxt[i]){
if(dfn[to[i]] == 0) {
dfs(to[i]);
low[u] = min(low[u], low[to[i]]);
}
else if(ins[to[i]]) low[u] = min(low[u], dfn[to[i]]);
// 只有v还在栈中（即还未形成ECC）的时候横叉边有效
// 只有有向图能产生有影响的横叉边，此时要特判对面是不是已经合并为SCC了，已经合并这条横叉边就无效了
// 可以证明，如果对面已经合并为SCC，则u不可能再与V形成更大的SCC
}
if(low[u] == dfn[u]){
int v; ++scc;
do{
v = stk[top--];
SCC[v] = scc;
ins[v] = 0;
++siz[scc];
}while(v != u);
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
adde(u, v);
}
for(int i = 1; i <= n; i++){
if(!dfn[i]) dfs(i);
}
int ans = 0 ;
for(int i = 1; i <= scc; i++)
if(siz[i] > 1) ans++;
cout << ans << endl;
return 0;
}
EBCC 边双连通分量
例题 P8436 【模板】边双连通分量
对于一个 \(n\) 个节点 \(m\) 条无向边的图，请输出其边双连通分量的个数，并且输出每个边双连通分量。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 14;
const int maxm = 4e6 + 14;
int n, m;
// 链式前向星
int head[maxm], nxt[maxm], to[maxm], tot = 1;
void adde(int u, int v){
nxt[++tot] = head[u];
to[head[u] = tot] = v;
}
int dfn[maxn], low[maxn], cnt;
bool brige[maxm]; // 某一条边是不是桥
void dfs(int u, int lst){
dfn[u] = low[u] = ++cnt;
for(int i = head[u]; i; i = nxt[i]){
if(i == lst) continue;
if(dfn[to[i]] == 0){
dfs(to[i], i ^ 1); // !! 注意写法，防止走同一条边回到父节点
low[u] = min(low[u], low[to[i]]);
if(low[to[i]] > dfn[u]) brige[i] = brige[i^1] = 1;
}
else low[u] = min(low[u], dfn[to[i]]);
}
}
bool vis[maxn]; // 某个点是否已经属于一个EBCC
vector < int > ans[maxn]; // 记录每个EBCC有哪些点
int EBCC; // EBCC计数
// 显然，不走桥能搜到的点都在同一个EBCC之中
void dfs2(int u){
ans[EBCC].push_back(u);
vis[u] = 1;
for(int i = head[u]; i; i = nxt[i]){
if(brige[i]) continue; // 如果这条边是桥就不走了
if(!vis[to[i]]) dfs2(to[i]);
}
}
int main(){
//freopen("1.in", "r", stdin);
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1, u, v; i <= m; i++){
cin >> u >> v;
adde(u, v);
adde(v, u);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) dfs(i, 0);
for(int i = 1; i <= n; i++)
if(!vis[i]){
++EBCC;
dfs2(i);
}
cout << EBCC << endl;
for(int i = 1; i <= EBCC; i++){
cout << ans[i].size() << " ";
for(auto u : ans[i]) cout << u << " ";
cout << endl;
}
return 0;
}
例题 P1656 炸铁路
按顺序输出无向图的所有桥
点击查看代码
#include<bits/stdc++.h>
using namespace std; // P1656
typedef long long ll; // 洛谷进阶篇std
const int maxn = 160;
const int maxm = 5050 * 2;
int n, m;
int head[maxn], to[maxm], nxt[maxm], tot = 1;
void adde(int u, int v){
nxt[++tot] = head[u];
to[head[u] = tot] = v;
}
int dfn[maxn], low[maxn], cnt;
int stk[maxn], top, bel[maxn]; // bel: 这个点属于哪个EBCC
int EBCC;
pair<int, int> brige[maxn]; int anscnt;
void dfs(int u, int lst){
dfn[u] = low[u] = ++cnt;
stk[++top] = u;
for(int i = head[u]; i; i = nxt[i]){
if(i == lst) continue;
if(!dfn[to[i]]){
dfs(to[i], i ^ 1);
low[u] = min(low[u], low[to[i]]);
if(low[to[i]] > dfn[u]) brige[++anscnt] = make_pair (min(u, to[i]), max(u, to[i]));
}
else low[u] = min(low[u], dfn[to[i]]);
}
if(low[u] == dfn[u]){
int v; ++EBCC;
do{
v = stk[top--];
bel[v] = EBCC;
}while(v != u);
}
}
bool cmp(pair<int, int> cmpx, pair<int, int> cmpy){
return cmpx.first == cmpy.first ? cmpx.second < cmpy.second : cmpx.first < cmpy.first;
}
int main(){
......
}
CF1000E We Need More Bosses
给定一个 \(n\) 个点 \(m\) 条边的无向图，保证图连通。找到两个点\(s,t\)，使得\(s\)到\(t\)必须经过的边最多（一条边无论走哪条路线都经过ta，这条边就是必须经过的边）
\(2<=n<=3*10^5,1<=m<=3*10^5\)
思路：缩EBCC求直径
dfs求直径复杂度爆炸了，换用bfs快了得有十倍
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 3e5 + 10;
const int maxm = 6e5 + 10;
int n, m;
int head[maxn], nxt[maxm], to[maxm], tot = 1;
void adde(int u, int v){
nxt[++tot] = head[u];
to[head[u] = tot] = v;
}
int dfn[maxn], low[maxn], cnt;
int stk[maxn], top;
int EBCC, bel[maxn];
void dfs(int u, int lst){
// tarjan求EBCC标准代码，不放了
}
vector < int > mp[maxn];
void bfs(int start, int &endpoint, int &maxdis) {
vector<int> dist(EBCC + 1, -1);
queue<int> q;
dist[start] = 0;
q.push(start);
maxdis = 0;
endpoint = start;
while (!q.empty()) {
int u = q.front(); q.pop();
if (dist[u] > maxdis) {
maxdis = dist[u];
endpoint = u;
}
for (int v : mp[u]) {
if (dist[v] == -1) {
dist[v] = dist[u] + 1;
q.push(v);
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1, x, y; i <= m; i++){
cin >> x >> y;
adde(x, y);
adde(y, x);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) dfs(i, 0);
for(int u = 1; u <= n; u++)
for(int i = head[u]; i; i = nxt[i])
if (i % 2 == 0) {
int v = to[i];
if(bel[u] != bel[v]) {
mp[bel[u]].push_back(bel[v]);
mp[bel[v]].push_back(bel[u]);
}
}
int A, B, maxdis;
bfs(1, A, maxdis);
bfs(A, B, maxdis);
cout << maxdis << endl;
return 0;
}
点双连通分量VBCC
例题 P8435 【模板】点双连通分量
点击查看代码
#include<bits/stdc++.h>
using namespace std; // P8435[模板]点双连通分量
typedef long long ll;
const int maxn = 5e5 + 10;
const int maxm = 4e6 + 10;
int n, m;
int head[maxn], nxt[maxm], to[maxm], tot;
void adde(int u, int v){
nxt[++tot] = head[u];
to[head[u] = tot] = v;
}
int dfn[maxn], low[maxn], cnt;
int stk[maxn], top;
int VBCC;
vector < int > Ans[maxn]; // 这里记录的是每个VBCC里边有谁
void dfs(int u, int fa){
dfn[u] = low[u] = ++cnt;
stk[++top] = u;
int son = 0;
for(int i = head[u]; i; i = nxt[i]){
if(to[i] == fa) continue;
if(!dfn[to[i]]){
++son;
dfs(to[i], u);
low[u] = min(low[u], low[to[i]]);
if(low[to[i]] >= dfn[u]){
// >= 表明u是一个割点，意义是子树为划分的结点无法到u的任何祖先
// 同时也表明，删掉u会导致子树v中没有划分的点形成点双连通分量
++VBCC;
while(stk[top] != to[i]) Ans[VBCC].push_back(stk[top--]);
Ans[VBCC].push_back(to[i]); --top;
Ans[VBCC].push_back(u);
// 注意此时u不能出栈了，因为他可能同时属于多个点双连通分量或者他是一个割点
// 不可能存在一个大于一个点的点集同时存在于两个VBCC中，或者说不存在一条边共存于两个VBCC
}
}
else low[u] = min(low[u], dfn[to[i]]);
}
// if(fa == 0 && son >= 2) 则根也是割点
// 下面这句这里特判的是图的孤立点
if(fa == 0 && son == 0) Ans[++VBCC].push_back(u);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= m; i++){
int u, v;
cin >> u >> v;
adde(u, v);
adde(v, u);
}
for(int i = 1; i <= n; i++){
top = 0; // 每次操作完割点可能会留在里边
if(!dfn[i]) dfs(i, 0);
}
cout << VBCC << endl;
for(int i = 1; i <= VBCC; i++){
cout << Ans[i].size();
for(auto u : Ans[i]){
cout << " " << u;
}
cout << endl;
}
return 0;
}
浙公网安备 33010602011771号