[SDOI 2011]消耗战[虚树][虚树学习笔记]

虚树（Virtual Tree）指在原树的基础上，选取部分点为 关键点，然后将这些点按照原树上的 父子关系 建树

不难发现，要想要保证 父子关系 不变化，虚树上除了 关键点 以外，还需要有一些关键点的 LCA，我们暂且称之为 LCA点

如图，红色点为 关键点，蓝色点是所必须的 LCA点，右图是左图的虚树

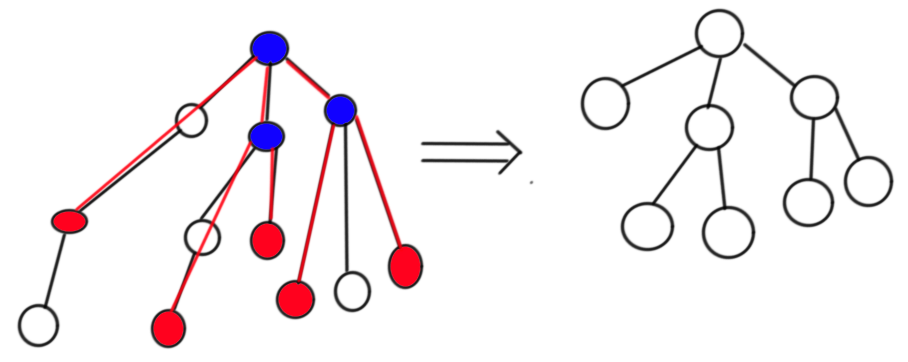
这样虚树上的一条边，在原树上代表一条链

可以发现如果关键点有 k 个，则整棵虚树最多只有 $2k-1$ 个点，这样构建出来的树可以用于剪掉一些不必要的情况

那么怎么建树？

---

对于一个点 u，如果它的几个儿子的子树中，有大于等于两个儿子的子树中有 key 点，那么这个点，就一定是 LCA点

这个感性理解一下大概挺显然的？

所以只需要一次 DFS，按照上述规则找到所有虚树上的点，再一遍 DFS 来连边即可

以 [SDOI 2019]世界地图 代码为例：

bool buildVT(int now, int f) { // 处理出所有虚树点
    int tot = isKey[now];
    // tot 是 自己是否是key点 与 有key点的子树 的数量和
    for(edge* e = g[now]; e; e = e->next) {
        int to = e->to;
        if(to == f) continue;
        tot += buildVT(to, now);
    }
    if(tot >= 2) isKey[now] = 1;
    return !!tot;
}

// 将上面处理出来的 key 连边形成虚树
// last 是上面的那个 key 点, max 是路径上的权值最大值
void processVal(int now, int f, int last, int max, std::vector <MSTedge>& V) {
    if(isKey[now]) {
        if(last) {
            V.push_back(MSTedge(now, last, max));
            ansdis -= max;
        }
        last = now, max = 0;
    }
    for(edge* e = g[now]; e; e = e->next) {
        int to = e->to;
        if(to == f) continue;
        processVal(to, now, last, std::max(max, e->val), V);
    }
    return;
}

复杂度：$O(n)$

---

然而这个复杂度很多时候不是很能接受

其实可以用栈来维护建树

首先要知道一个结论，从左到右的将 key 点排序后，虚树上的 LCA 点一定是某一对相邻的 key 的 LCA

我们用一个栈来维护当前这个点到根节点这条链上的所有点（或者被称为最右链，因为我们是从左到右处理）

一开始将第一个点直接压入栈中，然后从左向右的枚举 key 点，分情况讨论

以下图中，红色点为当前的 key 点，蓝色点是 栈顶点，绿色点是栈顶下面的那个点（栈中第二个点），黄色为栈中其他点，箭头指向 栈顶点 和 当前点 的 LCA

情况①：如图

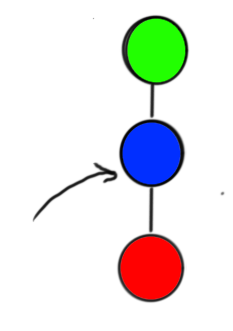
这种情况直接将当前点加入栈

情况②：如图

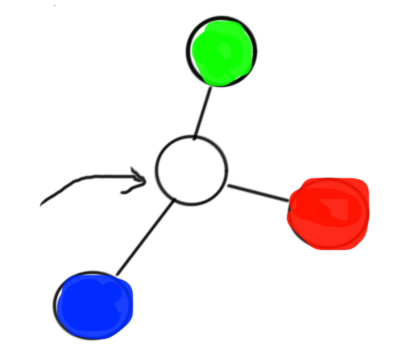
 这种情况把 lca 和 栈顶点 连个边然后扔掉 栈顶点 就好，然后栈中加入 lca 和 当前点

情况③：如图

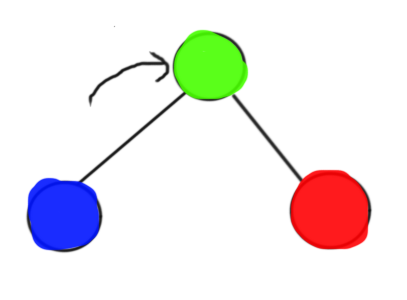
 和 ② 相同，不过 lca 点已经在栈中了，没必要入栈了

情况④：如图

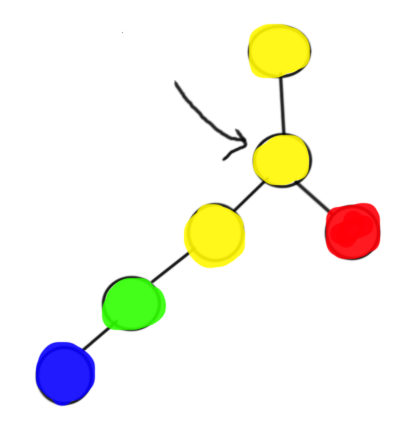
将左侧那条链全部连上边，然后全部出栈，再入当前点就好

复杂度：$O(k)$ （但还需要加上求 LCA 的复杂度）

---

[SDOI 2011]消耗战

简述题意：给定一棵树，边有边权，T 次询问，每次钦点 k 个点，要求断开若干条边（断开这条边需要花费这条边边权的费用），使得任意一个钦定点到根（1号点）不连通，求最小费用

数据范围：$n\leq 2.5\times 10^5, T\leq 5\times 10^5, \sum k\leq 5\times 10^5$

---

可以有树形 dp：

dp[i] 表示以 i 为根的子树中，i 与子树中钦定点不连通的最小花费

$dp[i]=dp[i]+\min\{dp[son_i], val(i\rightarrow son_i)\}$ （$son_i$ 不是钦定点）

$dp[i]=dp[i]+val(i\rightarrow son_i)$ （$son_i$ 是钦定点）

期望得分：40pts

这么做显然复杂度爆炸，考虑优化

发现这个 dp 中用了很多不必要的点，按照那些钦定点建一棵虚树，在虚树上跑 dp，能快非常多

dp 的时候式子也会有变化，$m(i)$ 表示从当前点到根节点的最小边权

$dp[i]=m(i)$ （叶子节点）

$dp[i] =\min\{\sum_{i}dp[son_i], m(i)\}$ （非叶子节点）

样例二即可 hack 该做法，原因是有若干个 key 点在虚树上形成了一个链

可以发现一个显然的结论，如果若干 key 点在虚树上形成链，假设这条链的顶端是 u 点，那么对于这道题来说，最优策略一定是用 $m(u)$ 的代价删除对应边

所以第一个式子应该改成

$dp[i]=m(i)$ （叶子节点或 key 点）

但是不知道是不是我自己的问题（），我获得了 MLE+TLE+WA 的好成绩

有另一种方法，就是建树的时候遇到 key 点就不向下建了，即 情况① 的时候直接跳出（详见代码）

不过似乎如果求 LCA 用倍增法的话好像有一些别的奇妙做法，但是我求 LCA 已经只会树剖了（

期望得分：100pts

复杂度：$O(mK\log K)$？

#include <ctime>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#define inf 500010
#define INF 0x7fffffffffffffff
#define ll long long

namespace chiaro{

using std::cerr;
using std::endl;
#define cerro(x) std::cerr << #x <<' '<< x << std::endl;

template <class I>
inline void read(I &num){
    num = 0; char c = getchar(), up = c;
    while(c < '0' || c > '9') up = c, c = getchar();
    while(c >= '0' && c <= '9') num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    up == '-' ? num = -num : 0; return;
}
template <class I>
inline void read(I &a, I &b) {read(a); read(b);}
template <class I>
inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}

struct edge {
    int to;
    ll val;
    edge* next;
};

struct Stack {
    ll a[inf];
    int ptr;

    inline void push(int x) {a[++ptr] = x;}
    inline void pop() {--ptr;}
    inline int top() {return a[ptr];}
    inline int topnext() {return a[ptr - 1];}
    inline int size() {return ptr;}
};

int n;
int key[inf];
int deg[inf];
bool book[inf];
edge* g[inf << 1];
edge* gv[inf << 1];
Stack S;

bool edgeClearFlag;
inline void connect(int from, int to, int val, edge** g) {
    static edge pool[inf << 2];
    static edge* p = pool;
    if(edgeClearFlag) p = pool, edgeClearFlag = 0;
    p->to = to;
    p->val = val;
    p->next = g[from];
    g[from] = p; p++;
    deg[from] += (val == 0);
    return;
}

namespace lcaWorker {
    int index;
    int fa[inf];
    int dfn[inf];
    int dep[inf];
    int top[inf];
    int son[inf];
    ll min[inf];
    int size[inf];

    void dfs1(int now, int f, int depth) {
        fa[now] = f;
        dep[now] = depth;
        size[now] = 1;
        int heavy = 0;
        for(edge* e = g[now]; e; e = e->next) {
            int y = e->to;
            if(y == f) continue;
            min[y] = std::min (e->val, min[now]);
            dfs1(y, now, depth + 1);
            size[now] += size[y];
            if(size[y] > heavy) {
                heavy = size[y];
                son[now] = y;
            }
        }
        return;
    }

    inline void dfs2(int now, int point) {
        dfn[now] = ++index;
        top[now] = point;
        if(son[now] == 0) return;
        dfs2(son[now], point);
        for(edge* e = g[now]; e; e = e->next) {
            int y = e->to;
            if(y == fa[now] || y == son[now]) continue;
            dfs2(y, y);
        }
        return;
    }

    inline int getLCA(int a, int b) {
        while(top[a] != top[b]) {
            if(dep[top[a]] < dep[top[b]]) b = fa[top[b]];
            else a = fa[top[a]];
        }
        return (dep[a] > dep[b] ? b : a);
    }
}

namespace VTree {
    using lcaWorker::dfn;
    using lcaWorker::dep;

    inline bool cmp(int a, int b) {return dfn[a] < dfn[b];}

    inline void build(int k) {
        std::sort(key + 1, key + 1 + k, cmp);
        S.push(1); S.push(key[1]);
        for(int i = 2; i <= k; i++) {
            int now = key[i];
            int lca = lcaWorker::getLCA(now, S.top());
            while(1) {
                if(dep[lca] >= dep[S.topnext()]) {
                    // break 建完整 VT, goto 建部分 VT
                    if(lca == S.top()) goto Line1;
                    else {
                        connect(lca, S.top(), 0, gv);
                        S.pop();
                        if(lca != S.top()) S.push(lca);
                    }
                    break;
                }
                connect(S.topnext(), S.top(), 0, gv);
                S.pop();
            }
            S.push(now);
            Line1:;
        }
        while(S.size() > 1) {
            connect(S.topnext(), S.top(), 0, gv);
            S.pop();
        }
        S.pop();
        return;
    }
}

namespace dpWorker {
    using lcaWorker::min;
    
    ll dp(int now) {
        if(deg[now] == 0) return min[now];
        ll cnt = 0;
        for(edge* e = gv[now]; e; e = e->next) {
            int to = e->to;
            cnt += dp(to);
        }
        gv[now] = NULL;
        deg[now] = 0;
        return std::min (min[now], cnt);
    }
}

inline void setting(){
#ifndef ONLINE_JUDGE
    freopen("_test.in", "r", stdin);
    freopen("_test.me.out", "w", stdout);
#endif
    return;
}

inline int main(){
    setting();
    read(n);
    for(int i = 1; i < n; i++) {
        int u, v, w;
        read(u, v, w);
        connect(u, v, w, g);
        connect(v, u, w, g);
    }
    lcaWorker::min[1] = INF;
    lcaWorker::dfs1(1, 0, 1);
    lcaWorker::dfs2(1, 1);
    int T; read(T);
    while(T--) {
        int k; read(k);
        for(int i = 1; i <= k; i++) {
            read(key[i]);
            book[key[i]] = 1;
        }
        VTree::build(k);
        printf("%lld\n", dpWorker::dp(1));
        edgeClearFlag = 1;
    }
    return 0;
}

}

signed main(){ return chiaro::main();}