莫比乌斯反演基础练习

Index：

1.莫比乌斯反演

2.luogu P2257

3.luogu P3911

迪利克雷卷积常用公式

 

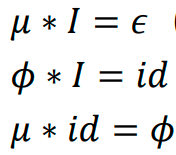
常用技巧：

1.增加枚举量（运用迪利克雷卷积等式）

2.交换枚举顺序

3.提取无关项

4.换元（存在两个需要不停计算使用的枚举量q,p的时候，尝试换元T=pq）（如例题2）

5.数论分块（如例题1）

P2257 YY的GCD

 

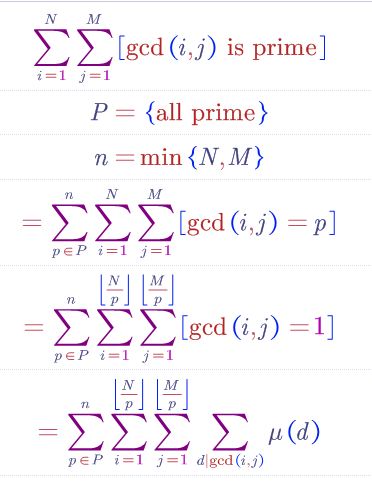
 预处理 f 然后直接数论分块即可

 1 #include <ctime>
 2 #include <cmath>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <cstdlib>
 6 #include <iostream>
 7 #include <algorithm>
 8 #include <cassert>
 9 #include <vector>
10 #include <queue>
11 #define inf 10000010
12 #define INF 0x7fffffff
13 #define ll long long
14 
15 namespace chiaro{
16 
17 template <class I>
18 inline void read(I &num){
19     num = 0; char c = getchar(), up = c;
20     while(c < '0' || c > '9') up = c, c = getchar();
21     while(c >= '0' && c <= '9') num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
22     up == '-' ? num = -num : 0; return;
23 }
24 template <class I>
25 inline void read(I &a, I &b) {read(a); read(b);}
26 template <class I>
27 inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}
28 
29 int n, m;
30 std::vector <int> prime;
31 int mu[inf];
32 ll f[inf], sum[inf];
33 
34 inline void shaiMu(int n) {
35     prime.reserve(665000);
36     static bool not_prime[inf];
37     not_prime[0] = not_prime[1] = 1;
38     mu[1] = 1;
39     for(int i = 1; i <= n; i++) {
40         if(not_prime[i] == 0) {
41             mu[i] = -1;
42             prime.push_back(i);
43         }
44         for(auto j: prime) {
45             if(1ll * i * j > n) break;
46             not_prime[i * j] = 1;
47             if(i % j == 0) {
48                 mu[i * j] = 0;
49                 break;
50             }
51             mu[i * j] = -mu[i];
52         }
53     }
54 }
55 
56 inline void getSum(int n) {
57     for(auto i: prime) {
58         for(int j = 1; j * i <= n; j++) f[i * j] += mu[j];
59     }
60     for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + f[i];
61 }
62 
63 inline void solve () {
64     read(n, m);
65     int N = std::min (n, m);
66     ll ans = 0;
67     for(int i = 1, j = 0; i <= N; i = j + 1) {
68         j = std::min (n / (n / i), m / (m / i));
69         ans += 1ll * (n / i) * (m / i) * (sum[j] - sum[i - 1]);
70     }
71     printf("%lld\n", ans);
72 }
73 
74 inline int main(){
75     int T; read(T);
76     shaiMu(1e7);
77     getSum(1e7);
78     while(T--) solve();
79     return 0;
80 }
81 
82 }
83 
84 signed main(){ return chiaro::main();}

P3911 最小公倍数之和

 

 

 

 

预处理 smu，现算 scnt 即可

 1 #include <ctime>
 2 #include <cmath>
 3 #include <cstdio>
 4 #include <cstring>
 5 #include <cstdlib>
 6 #include <iostream>
 7 #include <algorithm>
 8 #include <vector>
 9 #include <queue>
10 #define inf 100010
11 #define INF 0x7fffffff
12 #define ll long long
13 
14 namespace chiaro{
15 
16 template <class I>
17 inline void read(I &num){
18     num = 0; char c = getchar(), up = c;
19     while(c < '0' || c > '9') up = c, c = getchar();
20     while(c >= '0' && c <= '9') num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
21     up == '-' ? num = -num : 0; return;
22 }
23 template <class I>
24 inline void read(I &a, I &b) {read(a); read(b);}
25 template <class I>
26 inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}
27 
28 int n;
29 int a[inf], cnt[inf];
30 int mu[inf];
31 ll smu[inf];
32 
33 inline void shaiMu(int n) {
34     static bool not_prime[inf];
35     std::vector <int> prime;
36     not_prime[0] = not_prime[1] = 1;
37     mu[1] = 1;
38     for(int i = 2; i <= n; i++) {
39         if(not_prime[i] == 0) {
40             mu[i] = -1;
41             prime.push_back(i);
42         }
43         for(auto j: prime) {
44             if(j * i > n) break;
45             not_prime[j * i] = 1;
46             if(i % j == 0) {
47                 mu[i * j] = 0;
48                 break;
49             }
50             mu[i * j] = -mu[i];
51         }
52     }
53 }
54 
55 inline int main(){
56     read(n);
57     int tmp = 0;
58     for(int i = 1; i <= n; i++) {
59         read(a[i]);
60         ++cnt[a[i]];
61         tmp = std::max(tmp, a[i]);
62     }
63     n = tmp;
64     shaiMu(n);
65     for(int i = 1; i <= n; i++) {
66         for(int j = i; j <= n; j += i) {
67             smu[j] += 1ll * mu[i] * i;
68         }
69     }
70     ll ans = 0;
71     for(int T = 1; T <= n; T++) {
72         ll scnt = 0;
73         for(int i = 1, I = n / T; i <= I; i++) {
74             scnt += 1ll * i * cnt[i * T];
75         }
76         ans += 1ll * T * scnt * scnt * smu[T];
77     }
78     std::cout << ans << '\n';
79     return 0;
80 }
81 
82 }
83 
84 signed main(){ return chiaro::main();}

 

posted @ 2021-01-03 22:35  Chiaro  阅读(222)  评论(0)    收藏  举报