NOI-Online2021第一场题解

愤怒的小N

定义 $pop(n)$ 表示 n 二进制下 1 的个数

可以发现 $b_n=pop(n)\bmod(2)$

考虑去掉模运算，$b_n=\frac{1}{2}(1-(-1)^{pop(n)})$

那么可以有以下推导

可以将 n 二进制拆分成若干段，具体地，对于一个这样的数 $(10110)_2$

可以拆分成这些段：

$[(0)_2,(10000)_2)$

$[(10000)_2,(10100)_2)$

$[(10100)_2,(10110)_2)$

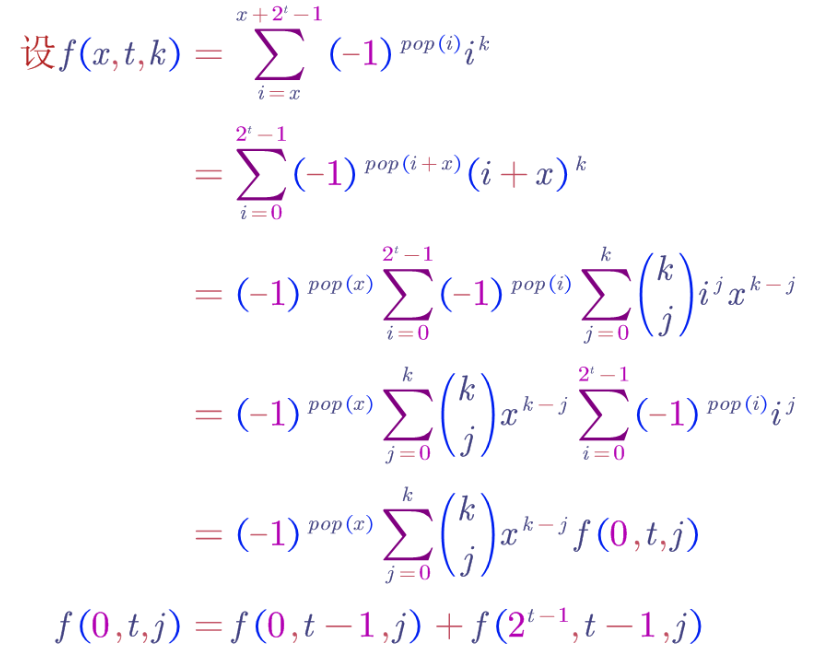
算算后发现复杂度是 $O(m^2\log n+m^3)$

通过打表发现或者归纳证明

当 $x>2^t$ 或者 $t>k$ 时，$f(x,t,k)=0$，所以 $f$ 的规模缩小到 O(m) 级别

复杂度 $O(m^3+\log n)$

---

积木小赛

考虑枚举 b 序列子区间，同时 a 数组用一个指针从左往右一路扫过去，复杂度 $O(n^2)$

关键在于如何子串判重，总共 $O(n^2)$ 个串需要 $O(1)$ 判重

手写哈希表即可，单模哈希可能被卡，写了个双模

#include <ctime>
#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <cassert>
#include <vector>
#include <queue>
#define inf 3007
#define INF 0x7fffffff
#define ll long long
#define uint unsigned int 

template <class I>
inline void read(I &num){
    num = 0; char c = getchar(), up = c;
    while(!isdigit(c)) up = c, c = getchar();
    while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    up == '-' ? num = -num : 0; return;
}
template <class I>
inline void read(I &a, I &b) {read(a); read(b);}
template <class I>
inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}

int n, ans;
char s[inf], t[inf];
const int P = 10025051;
const int BP = 1019260817;
const int base = 127;

class hashList {
    public:
    struct listNode {
        int nxt;
        ll v;
    };

    int head[P + 2];
    listNode lst[P + 2];
    int index;

    inline bool insert(ll x) {
        int d = x % P;
        if(head[d] == 0) {
            head[d] = ++index;
            lst[index].v = x;
            return 1;
        } else {
            int now = head[d];
            while(1) {
                if(lst[now].v == x) return 0;
                if(lst[now].nxt == 0) break;
                now = lst[now].nxt;
            }
            lst[now].nxt = ++index;
            lst[index].v = x;
            return 1;
        }
    }
};

hashList hl;

inline void setting(){
    freopen("block.in", "r", stdin);
    freopen("block.out", "w", stdout);
    return;
}

signed main(){
    // setting();
    read(n);
    scanf("%s%s", s + 1, t + 1);
    for(int l = 1; l <= n; l++) {
        int now = 0;
        int hash1 = 0;
        uint hash2 = 0;
        for(int r = l; r <= n; r++) {
            ++now;
            while(now <= n) {
                if(s[now] == t[r]) break;
                ++now;
            }
            if(now > n) break;
            hash1 = 1ll * (hash1 * base + t[r]) % BP;
            hash2 = (hash2 * base + t[r]);
            ans += hl.insert(1ll * hash2 * (1000000000) + hash1);
        }
    }
    std::cout << ans << '\n';
    return 0;
}