Smooth min-entropy

信息论的神奇妙妙工具——Smoothed entropy （平滑熵）

回顾min-entropy

首先有\(\infty\)-divergence

\[D_{\infty}(P \| Q) = \max_{x} \log \frac{P(x)}{Q(x)} \]

用\(D_{\infty}\)定义min-entropy

\[\begin{aligned} H_{\min}(X) &= - D_{\infty}(P_X\| 1) = -\log \max_{x} P_X(x) \\ H_{\min}^{\downarrow}(Y|X) &= - D_{\infty}(P_{XY}\|P_{X}) = - \log \max_{y} P_{Y|X}(y|x) \\ H_{\min}^{\uparrow}(Y|X) &= \max_{Q_X} - D_{\infty}(P_{XY}\|Q_X) \end{aligned} \]

smoothing 是什么？

从min-entropy的定义来看，这并不是一个有着良好行为的量，因为它只关注（条件）概率分布的最大值，这使得它容易受意外极值的影响。
像这两个分布

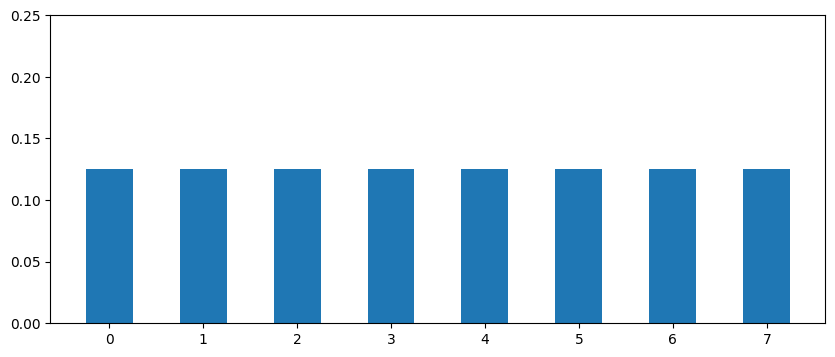
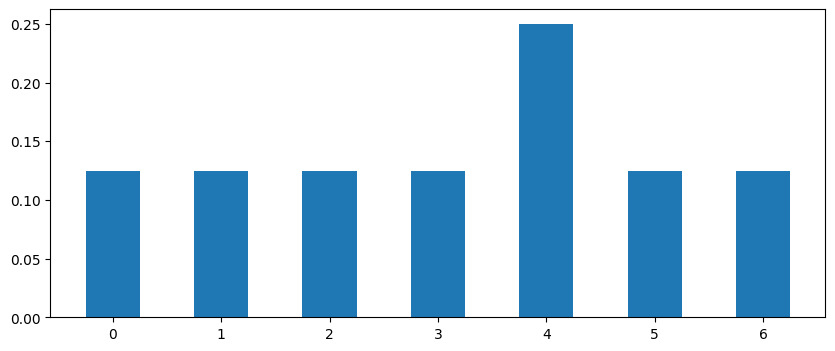
这两个分布的距离（total variation distance）只有1/8，但min-entropy分别为3，2。在样本量更大时这种效应会更加明显。例如\(n=1000\)的均匀分布\(P(x) = 1/1000，\text{for } x=1,\dots, 1000\)，与\(Q(1)=1/100,Q(x)=1/1000,\text{for } x=2,\dots,901\)，其min-entropy相差\(3.3\)但距离只有\(1/100\)。

为了避免min-entropy受个别意外值的影响，可以考虑\(P_X\)邻域的一些分布并取他们的min-entropy的最大值。邻域由total variation distance刻画

\[T(P,Q) = \frac{1}{2}\sum_{x}|P(x)-Q(x)| \]

\(P_X\)的邻域是一个半径为\(\varepsilon\)的“球”

\[\mathcal{B}^\varepsilon(P_X) = \{Q_X \mid \forall x, Q_X(x) \le P_X(x), T(P_X,Q_X) \le \varepsilon\} \]

（出于一些technical上的考虑，我们额外要求\(Q\)始终小于\(P\)）

于是可以定义smoothed min-entropy

\[\begin{aligned} H_{\min}^{\varepsilon}(X)_P &= \max_{Q_X \in \mathcal{B}^\varepsilon(P_X) } H_{\min}(X)_Q \\ H_{\min}^{\downarrow,\varepsilon} (Y|X)_P &= \max_{Q_{XY} \in \mathcal{B}^{\varepsilon}(P_{XY})} - D_{\infty}(Q_{XY}\| P_X) \\ H_{\min}^{\uparrow, \varepsilon} (Y|X)_P &= \max_{Q_{XY} \in \mathcal{B}^\varepsilon (P_{XY})} \max_{R_X} -D_{\infty}(Q_{XY} \| R_X) \end{aligned} \]

一些remark

• 注意\(H_{\min}^{\downarrow,\varepsilon}\)的定义中，\(\max\)后面的项为\(D_{\infty}(Q_{XY}\|P_{X})\)而非\(D_{\infty}(Q_{XY}\|Q_{X})\)。
• 在\(H_{\min}^{\uparrow, \varepsilon}\)的定义中，第一个\(\max\)是over subnormalized \(Q_{XY}\)，第二个\(\max\)是over normalized \(R_{X}\)(\(R_X\)必须归一化)。

简单应用：用smoothed min-entropy重新表述渐进均分性（AEP）

完整的渐进均分性还需要用到max-entropy，我们这里只一窥其貌，使用AEP推导出\(H^{\varepsilon}_{\min}\)在独立同分布变量下的渐进行为。
设\(X^n\)为\(n\)个独立同分布随机变量，根据AEP，有

\[\Pr\left[ 2^{-n(H(X)+\delta)} \le P_{X^n}(X^n) \le 2^{-n(H(X)-\delta)} \right] \ge 1-\varepsilon \]

或者

\[\Pr\left[ X^n \in \mathcal{T}^n_\delta \right] \ge 1-\varepsilon \]

其中\(\mathcal{T}^n_\delta\)为典型集，\(\delta\)可以任意小，\(\varepsilon\)与\(\delta\)的关系由concentration inequality给出（例如Hoeffding's inequality）。

根据smoothed min-entropy的定义，构造一个截断后的\(P_{X^n}\)

\[Q_{X^n}(x^n) = \begin{cases} P_{X^n}(x^n), & x^n \in \mathcal{T}^n_\delta \\ 0, & \text{otherwise} \end{cases} \]

显然\(Q_{X^n} \in \mathcal{B}^\varepsilon(P_{X^n})\)，因此

\[H_{\min}^{\varepsilon}(X^n)_P \ge H_{\min}(X^n)_Q \ge n(H(X)-\delta) \]

可以看出在渐进条件下，\(H_{\min}^{\varepsilon}(X^n)_P\)会接近\(nH(X)\)，事实上我们有

\[\lim_{\varepsilon \to 0}\lim_{n \to \infty} \frac{1}{n} H_{\min}^{\varepsilon}(X^n) = H(X) \]