排序算法Java代码实现（六）—— 堆排序

本片内容：

• 堆排序

 堆排序

最大堆：

　　二叉堆是完全二叉树或者是近似完全二叉树，

　　当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。（父节点大于任何一个子节点）

算法思想：

1. 把n个元素建立最大堆，把堆顶元素A[0]与待排序序列的最后一个数据A[n-1]交换；
2. 把剩下的n-1个元素重新建立最大堆，把堆顶元素A[0]与待排序序列的最后一个元素A[n-2]交换；
3. 把剩下的n-2个元素重新建立最大堆，把堆顶元素A[0]与待排序序列的最后一个元素A[n-3]交换；

重复以上步骤，直到把最后两个元素建成最大堆并进行交换，得到的序列就是排序后的有序序列。

代码实现：

/**
 * 
 */
package com.cherish.SortingAlgorithm;

/**
 * @author acer
 *
 */
public class Chapter_7_堆排序 extends ArrayBase {

    /**
     * @param args
     */
    public static void main(String[] args) {
        // TODO 自动生成的方法存根
        int[] array = new int[] {3,4,7,9,2,5,1,8,6};
        heapSorting(array);
        printArray(array);

    }
    
    //堆排序
    public static void heapSorting(int[] array)
    {
        int arrayLength = array.length;
        //循环建堆
        for(int i = 0;i < arrayLength-1;i++) 
        {
            //建堆，建一次最大堆，寻找一个待排序列的最大数
            buildMaxHeap(array,arrayLength-1-i);
            //交换堆顶元素（带排序序列的最大数）和最后一个元素  array[0]是堆顶
            swap(array,0,arrayLength-1-i);
            
        }
    }
    
    //建最大堆
    public static void buildMaxHeap(int[] array,int lastIndex)
    {
        //从最后一个节点（index）的父节点开始
        for(int i = (lastIndex-1)/2 ; i >= 0; i--)
        {
            //k 保存正在判断的节点
            int k = i;
            //如果当前k节点的子节点存在
            while(k*2+1 <= lastIndex)
            {
                //k节点的左子节点的索引
                int biggerIndex = 2*k + 1;
                //如果k节点的左子节点biggerIndex小于index,即biggerIndex+1代表的k节点的右子节点存在
                if(biggerIndex < lastIndex)
                {
                    //若右子节点的值较大
                    if(array[biggerIndex]<array[biggerIndex + 1])
                    {
                        //biggerIndex总是记录较大子节点的索引
                        biggerIndex = biggerIndex + 1;
                    }
                }
                //如果k节点的值小于其较大的子节点的值，交换他们
                if(array[k] < array[biggerIndex])
                {
                    swap(array,k,biggerIndex);
                    //将biggerIndex赋予k，开始while循环的下一次循环，重新保证k节点的值大于其左右子节点的值
                    k = biggerIndex;
                }else
                {
                    //当前判断节点k(父节点)大于他的两个子节点时，跳出while循环
                    break;
                }
                
            }
        }
    }
}

 

实现结果：

 

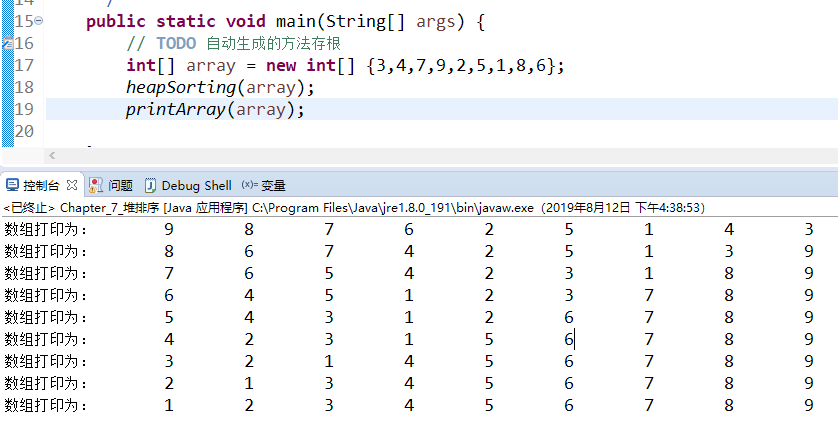
 由上图可以看到，每次建立最大堆时，最大的数都在array[0],下一次建堆时，上一个最大的数已经移到数组尾部了。