网络流、最大流、费用流

网络流、最大流、费用流

目录

• 网络流、最大流、费用流
  • \(1.\) 网络流概念
    • \(1.1\) 网络
    • \(1.2\) 流
    • \(1.3\) 残余网络
    • \(1.4\) 增广路
    • \(1.5\) 反悔边
    • \(1.6\) 最大流算法
  • \(2.\ Ford-Fulkerson\ Algorithm\)
    • \(2.1\) \(FF\) 算法概括
    • \(2.2\) \(FF\ code\)
    • \(2.3\) \(FF\) 时间复杂度及瓶颈
  • \(3.\ Edmond-Karp\ Algorithm\)
    • \(3.1\) \(EK\) 算法概括
    • \(3.2\) \(EK\ code\)
    • \(3.3\) \(EK\) 时间复杂度及瓶颈
  • \(4.\ Dinic\ Algorithm\)
    • \(4.1\) \(Dinic\) 算法概述
    • \(4.2\) \(Dinic\) 的特点以及其他优化
      • \(4.2.1\) 多路增广
      • \(4.2.2\) 分层图
      • \(4.2.3\) 可行性剪枝
      • \(4.2.4\) 当前弧优化
    • \(4.3\) \(Dinic\ code\)
    • \(4.4\) \(Dinic\) 时间复杂度

\(1.\) 网络流概念

\(1.1\) 网络

网络指的是有向图 \(G(V,\ E)\)

每条边 \((u,\ v)\in E\) 都有一个权值 \(w(u,\ v)\)，称之为容量

两个特殊的点为源点 \(s\) 和汇点 \(t\)

\(1.2\) 流

定义 \(f(u,\ v)\) 为流经边 \((u,\ v)\) 的流量

流量满足

• 正反流量互为相反数，即 \(f(u,\ v) = -f(v,\ u)\)
• 流量限制，即 \(f(u,\ v)\leq w(u,\ v)\)
• 流量守恒，即流出点的流量和流入该点的流量相等
• 若边 \((u,\ v)\) 流过一个大小为 \(f(u,\ v)\) 的流，那么该边剩余的容量为 \(w(u,\ v) - f(u,\ v)\)

可行流指的就是能从源点 \(s\) 汇入汇点 \(t\) 的一个流量

最大流指的就是可行流的最大值

\(1.3\) 残余网络

网络上所有边的容量减去可行流的大小，得到的新的网络被称为残余网络

\(1.4\) 增广路

网络中能使可行流增加的一条路径被称为增广路

\(1.5\) 反悔边

经典图如下

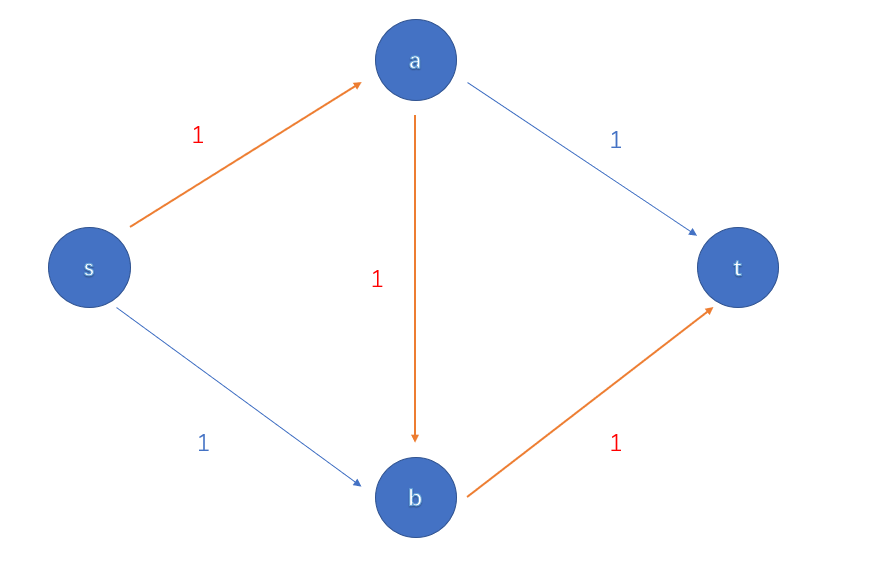
走红线标注的路显然不是流量最大

考虑引入反悔边

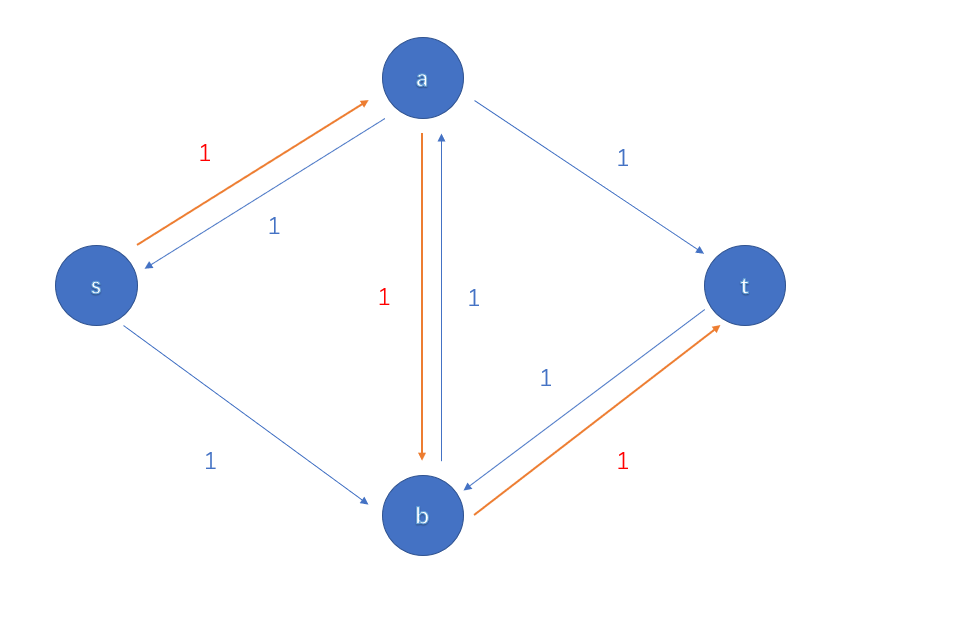
反悔可以认为是决策的重构，边 \((a,\ b)\) 的流量对答案的贡献并没有变化，所以这是正确的

不得不说，反悔边真是一个天才的想法

\(1.6\) 最大流算法

不断寻找增广路，同时建立反悔边

当无法找到增广路时，流量达到最大值

\(2.\ Ford-Fulkerson\ Algorithm\)

\(2.1\) \(FF\) 算法概括

• 用 \(dfs\) 寻找增广路
• 建立反悔边
• 重复上述过程

\(2.2\) \(FF\ code\)

/*FF Algorithm*/
#include <bits/stdc++.h>
#define fi first
#define se second
#define pii pair<int, int>
#define arrayDebug(a, l, r) for(int i = l; i <= r; ++i) printf("%d%c", a[i], " \n"[i == r])
typedef long long LL;
typedef unsigned long long ULL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int inf = 0x3f3f3f3f;
const int DX[] = {0, -1, 0, 1, 0, -1, -1, 1, 1};
const int DY[] = {0, 0, 1, 0, -1, -1, 1, 1, -1};
const int MOD = 1e9 + 7;
const int N = 2e5 + 7;
const double PI = acos(-1);
const double EPS = 1e-6;
using namespace std;
inline int read()
{
    char c = getchar();
    int ans = 0, f = 1;
    while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
    while(isdigit(c)) {ans = ans * 10 + c - '0'; c = getchar();}
    return ans * f;
}

int n, m, s, t, cnt, head[N], vis[N];
struct edge
{
    int fr, to, next, w;
}e[N];

void addedge(int a, int b, int c)
{
    e[cnt].fr = a;//第一条边标为 1
    e[cnt].to = b;
    e[cnt].w = c;
    e[cnt].next = head[a];
    head[a] = cnt++;
}

int dfs(int u = s, int flow = inf)
{
    if(u == t) return flow;
    vis[u] = 1;
    for(int i = head[u]; ~i; i = e[i].next){
        int v = e[i].to;
        if(e[i].w == 0 || vis[v]) continue;
        int res = dfs(v, min(flow, e[i].w));
        if(res > 0) {
            e[i].w -= res;
            e[i ^ 1].w += res;
            return res;
        }
    }
    return 0;
}

int FF()
{
    int res = dfs(), ans = 0;
    while(res > 0) {
        memset(vis, 0, sizeof(vis));
        ans += res;
        res = dfs();
    }
    return ans;
}

int main()
{
    memset(head, -1, sizeof(head));
    scanf("%d %d %d %d", &n, &m, &s, &t);
    for(int i = 1; i <= m; ++i) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        addedge(a, b, c);
        addedge(b, a, 0);
    }
    printf("%d\n", FF());
    return 0;
}

\(2.3\) \(FF\) 时间复杂度及瓶颈

每次增广，至少增加 \(1\) 的流量

每次增广，最多流经 \(m\) 条边

所以理论复杂度为 \(O(CM)\)，其中 \(C\) 为流量，\(M\) 为边数

如果流量特别大，那么这样的复杂度显然是不够优秀的

如下所示

\(3.\ Edmond-Karp\ Algorithm\)

\(3.1\) \(EK\) 算法概括

• \(bfs\) 找最近的增广路
• 建立反边
• 重复上述过程

\(3.2\) \(EK\ code\)

/*EK Algorithm*/
#include <bits/stdc++.h>
#define fi first
#define se second
#define pii pair<int, int>
#define arrayDebug(a, l, r) for(int i = l; i <= r; ++i) printf("%d%c", a[i], " \n"[i == r])
typedef long long LL;
typedef unsigned long long ULL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int inf = 0x3f3f3f3f;
const int DX[] = {0, -1, 0, 1, 0, -1, -1, 1, 1};
const int DY[] = {0, 0, 1, 0, -1, -1, 1, 1, -1};
const int MOD = 1e9 + 7;
const int N = 2e5 + 7;
const double PI = acos(-1);
const double EPS = 1e-6;
using namespace std;
inline int read()
{
    char c = getchar();
    int ans = 0, f = 1;
    while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
    while(isdigit(c)) {ans = ans * 10 + c - '0'; c = getchar();}
    return ans * f;
}

int n, m, s, t, cnt, head[N], vis[N], pre[N];
struct edge
{
    int fr, to, next, w;
}e[N];

void addedge(int a, int b, int c)
{
    e[cnt].fr = a;//第一条边标为 1
    e[cnt].to = b;
    e[cnt].w = c;
    e[cnt].next = head[a];
    head[a] = cnt++;
}

int bfs(int u = s)
{
    memset(vis, 0, sizeof(vis));
    memset(pre, -1, sizeof(pre));
    vis[u] = 1;
    queue<int> q;
    q.push(u);
    while(!q.empty()) {
        int temp = q.front(); q.pop();
        if(temp == t) break;
        for(int i = head[temp]; ~i; i = e[i].next) {
            if(vis[e[i].to] || e[i].w == 0) continue;
            vis[e[i].to] = 1;
            pre[e[i].to] = i; //记录点 x 的前驱边的序号
            q.push(e[i].to);
        }
    }
    int flow = inf;
    for(int i = pre[t]; ~i; i = pre[e[i].fr]) //找出流量
        flow = min(flow, e[i].w);
    if(flow == inf) return 0;
    for(int i = pre[t]; ~i; i = pre[e[i].fr]) { //建立反边
        e[i].w -= flow;
        e[i ^ 1].w += flow;
    }
    return flow;
}

int EK()
{
    int res = bfs(), ans = 0;
    while(res > 0) {
        ans += res;
        res = bfs();
    }
    return ans;
}
int main()
{
    memset(head, -1, sizeof(head));
    scanf("%d %d %d %d", &n, &m, &s, &t);
    for(int i = 1; i <= m; ++i) {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        addedge(a, b, c);
        addedge(b, a, 0);
    }
    printf("%d\n", EK());
    return 0;
}
/*
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
*/

\(3.3\) \(EK\) 时间复杂度及瓶颈

\(O(NM^2)\)，其中 \(N\) 为顶点数，\(M\) 为边数

当边数 \(M\) 特别大时，这样的复杂度是不够优秀的

\(4.\ Dinic\ Algorithm\)

\(4.1\) \(Dinic\) 算法概述

• 先用 \(bfs\) 对网络图分层，即预处理出每个点相对于源点的距离
• 然后用 \(dfs\) 多路增广，同时建立反边，直到当前图没有流量为止
• 重复上述过程

多路增广的含义是，不是找到一个流量就返回，而是要穷尽当前网络的所有流量才返回

\(4.2\) \(Dinic\) 的特点以及其他优化

\(4.2.1\) 多路增广

相较于传统 \(dfs\) 寻找增广路，多路增广实际上找出了一个增广路网

\(4.2.2\) 分层图

设立分层图的本质就是预处理每个点相对于源点的距离

这样流量在流动时避免“绕路”，而是直接流向更远的点

\(4.2.3\) 可行性剪枝

若当前点流出的剩余流量为零，那么无法继续向下传输流量

所以直接退出循环，回溯到上一层

\(4.2.4\) 当前弧优化

多路增广时，已经增广的路径可能会被再次访问

用 \(cur\) 数组记录点 \(u\) 已经被增广的出边，下次直接从未被增广的出边开始增广

for(int &i = cur[u]; ~i; i = e[i].next) {
    ...
}

注意到这里的引用取值

随着 \(i\) 增加，\(cur[i]\) 也会增加，于是起到了记录的作用

值得一提的是，当前弧优化的优化效果相当不错

\(4.3\) \(Dinic\ code\)

/*Dinic Algorithm*/
#include <bits/stdc++.h>
#define fi first
#define se second
#define pii pair<int, int>
#define arrayDebug(a, l, r) for(int i = l; i <= r; ++i) printf("%d%c", a[i], " \n"[i == r])
typedef long long LL;
typedef unsigned long long ULL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int inf = 0x3f3f3f3f;
const int DX[] = {0, -1, 0, 1, 0, -1, -1, 1, 1};
const int DY[] = {0, 0, 1, 0, -1, -1, 1, 1, -1};
const int MOD = 1e9 + 7;
const int N = 2e5 + 7;
const double PI = acos(-1);
const double EPS = 1e-6;
using namespace std;
inline int read()
{
    char c = getchar();
    int ans = 0, f = 1;
    while(!isdigit(c)) {if(c == '-') f = -1; c = getchar();}
    while(isdigit(c)) {ans = ans * 10 + c - '0'; c = getchar();}
    return ans * f;
}

int n, m, s, t, cnt, head[N], dep[N], cur[N];
struct edge
{
    int fr, to, next, w;
}e[N];

void addedge(int a, int b, int c)
{
    e[cnt].fr = a;//第一条边标为 0，对应反边为 1
    e[cnt].to = b;
    e[cnt].w = c;
    e[cnt].next = head[a];
    head[a] = cnt++;
}

void debug()
{
    for(int i = 1; i <= n; ++i){
        cout<<i<<": ";
        for(int j = head[i]; ~j; j = e[j].next)
            printf("(%d, %d, %d)", e[j].fr, e[j].to, e[j].w);
        puts("");
        cout<<dep[i]<<endl;
    }
    puts("");
}

bool bfs()
{
    memset(dep, 0, sizeof(dep)); //dep 有标记，则可以访问到该点
    queue<int> q; q.push(s);
    dep[s] = 1;
    while(!q.empty()) {
        int u = q.front(); q.pop();
        for(int i = head[u]; ~i; i = e[i].next) {
            int v = e[i].to, cost = e[i].w;
            if(cost && !dep[v]) dep[v] = dep[u] + 1, q.push(v);
        }
    }
    return dep[t];
}

int dfs(int u = s, int flow = inf)
{
    if(u == t) return flow;
    int ans = 0;
    for(int &i = cur[u]; ~i; i = e[i].next) {
        int v = e[i].to, cost = e[i].w;
        if(dep[v] == dep[u] + 1 && cost) {
            int res = dfs(v, min(flow, cost));
            if(res > 0) {
                e[i].w -= res, e[i ^ 1].w += res; //建立反边
                flow -= res; //可以流通的流量减少
                ans += res; //答案的贡献增加
                if(!flow) break; //没有可以流通的流量，直接退出循环
            }
        }
    }
    return ans;
}

int Dcnic()
{
    int ans = 0;
    while(bfs()) {
        memcpy(cur, head, sizeof(head));
        ans += dfs();
    }
    return ans;
}

int main()
{
    memset(head, -1, sizeof(head));
    n = read(), m = read(), s = read(), t = read();
    for(int i = 1; i <= m; ++i) {
        int a, b, c;
        a = read(), b = read(), c = read();
        addedge(a, b, c);
        addedge(b, a, 0);
    }
    printf("%d\n", Dcnic());
    return 0;
}
/*
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40
*/

\(4.4\) \(Dinic\) 时间复杂度

\(O(N^2M)\)，其中 \(N\) 为顶点数，\(M\) 为边数