链式前向星

链式前向星

链式前向星其实就是用另一种方式实现邻接表，而且是头插法。

将结点按 \(1\sim n\) 依次编号，表头数组 h[i] 表示点 \(i\) 的第一条出边。

边集数组 e[k] 存储第 \(k\) 条边的终点 \(v\) ，边权 \(w\) 和下一条边 \(ne\)。

边的编号 idx 可取 \(0,1,2,3\cdots\)。

时间复杂度和空间复杂度都是 \(O(n + m)\)。

应用：各种图，能处理反向边。

#include <bits/stdc++.h>
using namespace std;

int n, m;// 点和边的个数
const int N = 1e5 + 5;// 点最多个数
const int M = 2e5 + 5;// 边最多条数
struct edge {int v, w, ne;};
edge e[M];// 边集
int idx, h[N];// 点的第一条出边

void add(int a, int b, int c)
{
	e[idx] = {b, c, h[a]};
	h[a] = idx++;// 表头指向第idx条边，idx更新自增
}

void dfs(int u, int fa)
{
    // 遍历所有出边
	for (int i = h[u]; ~i; i = e[i].ne) {
		int v = e[i].v, w = e[i].w;
		if (v == fa) continue;
		cout << u << " " << v << " " << w << '\n';
        // 以v为起点，u为父节点dfs
		dfs(v, u);
	}
}

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	memset(h, -1, sizeof(h));// 表头初始化为-1，表示点的出边全部遍历完，初始为0条
	int a, b, c;
	for (int i = 1; i <= m; i++) {
        // 输入边的起点、终点和边权
		cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);// 反向边
	}
	dfs(1, 0);// 从第1个点开始dfs，没有父节点，fa=0即可
	return 0;
}

输入

6 5
4 3 90
1 4 30
5 6 60
1 5 20
5 2 70

输出

1 5 20
5 2 70
5 6 60
1 4 30
4 3 90

图片来源：【B02 图的存储——信息学奥赛算法】

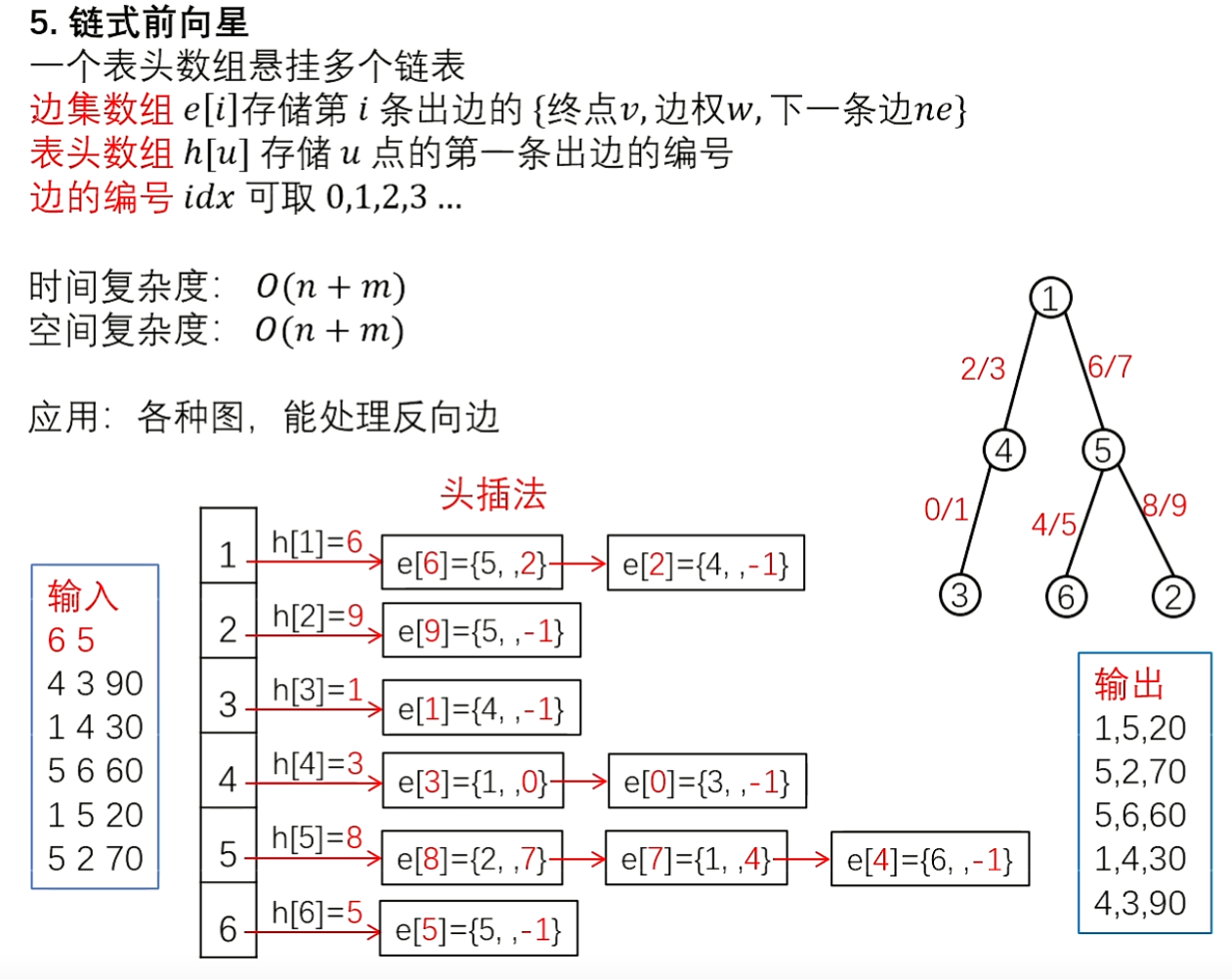
会发现，图中边的编号为 \(a/b\) 的形式，实际上在构建图的时候把每条边都算了反向边。

保证了叶子结点（比如这个树图）能返回到父节点，比如叶子结点2,5从边8到2，再从边9到5，实现回溯。

到父节点继续剪枝，继续遍历父节点的出边。