双向广搜 P1032 洛谷 [NOIP 2002 提高组] 字串变换

双向广搜 P1032 洛谷 [NOIP 2002 提高组] 字串变换

题目背景

本题不保证存在靠谱的多项式复杂度的做法。测试数据非常的水，各种做法都可以通过，不代表算法正确。因此本题题目和数据仅供参考。

本题为搜索题，本题不接受 hack 数据。关于此类题目的详细内容

题目描述

已知有两个字串 \(A,B\) 及一组字串变换的规则（至多 \(6\) 个规则），形如：

• \(A_1\to B_1\)。
• \(A_2\to B_2\)。

规则的含义为：在 \(A\) 中的子串 \(A_1\) 可以变换为 $ B_1\(，\)A_2$ 可以变换为 \(B_2\cdots\)。

例如：\(A=\texttt{abcd}\)，\(B＝\texttt{xyz}\)，

变换规则为：

• \(\texttt{abc}\rightarrow\texttt{xu}\)，\(\texttt{ud}\rightarrow\texttt{y}\)，\(\texttt{y}\rightarrow\texttt{yz}\)。

则此时，\(A\) 可以经过一系列的变换变为 \(B\)，其变换的过程为：

• \(\texttt{abcd}\rightarrow\texttt{xud}\rightarrow\texttt{xy}\rightarrow\texttt{xyz}\)。

共进行了 \(3\) 次变换，使得 \(A\) 变换为 \(B\)。

输入格式

第一行有两个字符串 \(A,B\)。

接下来若干行，每行有两个字符串 \(A_i,B_i\)，表示一条变换规则。

输出格式

若在 \(10\) 步（包含 \(10\) 步）以内能将 \(A\) 变换为 \(B\)，则输出最少的变换步数；否则输出 NO ANSWER!。

输入输出样例 #1

输入 #1

abcd xyz
abc xu
ud y
y yz

输出 #1

3

说明/提示

对于 \(100\%\) 数据，保证所有字符串长度的上限为 \(20\)。

【题目来源】

NOIP 2002 提高组第二题

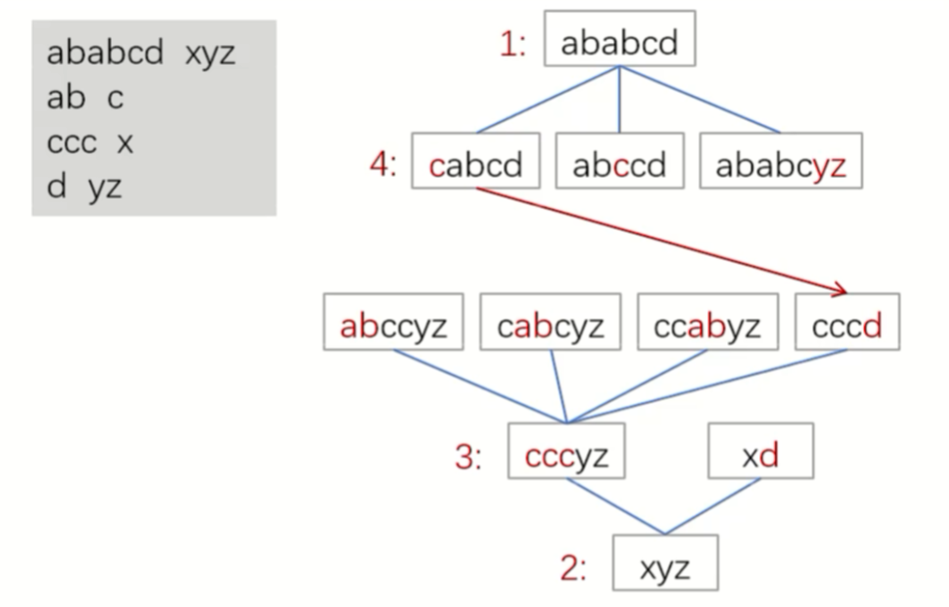
思路

双向BFS。

初始串 \(A\) ，目标串 \(B\) 。

规则拿循环输入，存入string数组里，并计数规则个数，分别为 \(a[N]，b[N]\) 。

代码关键在于extend函数的编写和参数调用。

所有有关队列和哈希的参数都是引用，按照队列大小安排。

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 6;
string A, B;
string a[N], b[N];
int n;

int extend( queue<string> &q,
            unordered_map<string, int> &ma,
            unordered_map<string, int> &mb,
            string a[N], string b[N])
{
    int m = q.size();
    while (m--) {
        string t = q.front();
        q.pop();
        int step = ma[t];

        for (int i = 0; i < n; i++) {// 枚举规则
            for (int j = 0; j < t.size(); j++) {// 遍历字符串
                if (t.substr(j, a[i].size()) == a[i]) {// 找到匹配规则
                    string tmp = t.substr(0, j) + b[i] + t.substr(j + a[i].size());
                    if (ma.count(tmp)) continue;
                    if (mb.count(tmp)) return step + mb[tmp] + 1;
                    // 两边哈希都没有
                    q.push(tmp);
                    ma[tmp] = step + 1;
                }
            }
        }
    }
    return 11;
}

int bfs()
{
    if (A == B) return 0;
    queue<string> qa, qb;
    unordered_map<string, int> ma,mb;
    qa.push(A), qb.push(B);
    ma[A] = mb[B] = 0;
    int mstep = 10, t;// 最大匹配步数10
    while (mstep--) {
        if (qa.size() <= qb.size()) t = extend(qa, ma, mb, a, b);
        else t = extend(qb, mb, ma, b, a);
        if (t <= 10) return t;
    }
    return 11;
}

int main()
{
    cin >> A >> B;
    while (cin >> a[n] >> b[n]) n++;
    int ans = bfs();
    if (ans == 11) cout << "NO ANSWER!" << endl;
    else cout << ans << endl;
    return 0;
}