省选模拟
省选模拟之辞旧迎新1
A. 神必的集合
不太理解
code
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cassert>
#include<cstring>
#include<complex>
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define int long long
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 405;
const int mod = 998244353;
void add(int &x, int y){x += y; if(x >= mod)x -= mod;}
int n, m, rk[maxn], a[maxn], f[65], dp[65][65], p2[65];
void ins(int x){
for(int i = n - 1; i >= 0; --i)if((x >> i) & 1){
if(!f[i])f[i] = x, i = 0;
else x ^= f[i];
}
}
int solve(){
for(int i = 0; i <= n; ++i)p2[i] = (1ll << n) - 1;
for(int i = 1; i <= m; ++i)ins(a[i]);
int mx = 0;
for(int j = 1; j <= m; ++j){
int nowa = a[j], d = rk[j];
for(int i = 0; i < n; ++i){
if((d >> i) & 1)p2[i + 1] &= nowa, mx = max(mx, i + 1);
else p2[i + 1] &= (p2[0] ^ nowa);
}
}
if(!f[0])dp[0][0] = 1; if(p2[1] & 1)dp[0][1] = 1;
for(int i = 1; i < n; ++i){
if(f[i]){
for(int j = 1; j <= i + 1; ++j)if((p2[j] >> i) & 1)
add(dp[i][j], dp[i - 1][j - 1]);
}else{
for(int j = 1; j <= i + 1; ++j)if((p2[j] >> i) & 1)
add(dp[i][j], (1ll << (i + 1 - j)) % mod * dp[i - 1][j - 1] % mod);
for(int j = 0; j <= i; j++)add(dp[i][j], dp[i - 1][j]);
}
}
int ans = 0;
for(int i = mx; i <= n; ++i)
add(ans, dp[n - 1][i]);
return ans;
}
signed main(){
freopen("set.in","r",stdin);
freopen("set.out","w",stdout);
n = read(), m = read();
for(int i = 1; i <= m; ++i)rk[i] = read() - 1, a[i] = read();
printf("%d\n", solve());
return 0;
}
B. 法阵
原题见
https://www.cnblogs.com/Chencgy/p/16760114.html
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
const int maxn = 500005;
int a[maxn], n;
struct query{
int l, r, id;
friend bool operator < (const query &x, const query &y){
return x.l > y.l;
}
}q[maxn];
struct seg{
struct node{
ll tag, val, mx;
}t[maxn << 2 | 1];
void push_up(int x){
t[x].mx = max(t[x << 1].mx, t[x << 1 | 1].mx);
t[x].val = max(t[x << 1].val , t[x << 1 | 1].val);
}
void built(int x, int l, int r){
if(l == r){
t[x].mx = a[l];
return;
}
int mid = (l + r) >> 1;
built(x << 1, l, mid);
built(x << 1 | 1, mid + 1, r);
push_up(x);
}
void upd(int x, ll val){
t[x].tag = max(t[x].tag, val);
t[x].val = max(t[x].val, t[x].mx + val);
}
void push_down(int x){
upd(x << 1, t[x].tag);
upd(x << 1 | 1, t[x].tag);
t[x].tag = 0;
}
void modify(int x, int l, int r, int L, int R, ll val){
if(L > R)return;
if(L <= l && r <= R){
upd(x, val);
return;
}
if(t[x].tag)push_down(x);
int mid = (l + r) >> 1;
if(L <= mid)modify(x << 1, l, mid, L, R, val);
if(R > mid)modify(x << 1 | 1, mid + 1, r, L ,R, val);
push_up(x);
}
ll query(int x, int l, int r, int L, int R){
if(L <= l && r <= R)return t[x].val;
if(t[x].tag)push_down(x);
int mid = (l + r) >> 1;
ll ans = 0;
if(L <= mid)ans = max(ans, query(x << 1, l, mid, L, R));
if(R > mid)ans = max(ans, query(x << 1 | 1, mid + 1, r, L, R));
return ans;
}
}t;
int sta[maxn], top;
ll ans[maxn];
void pop(int x){
t.modify(1, 1, n, sta[top] + sta[top] - x, n, a[sta[top]] + a[x]);
--top;
}
void push(int x){
if(top)t.modify(1, 1, n, sta[top] + sta[top] - x, n, a[sta[top]] + a[x]);
sta[++top] = x;
}
int main(){
freopen("fz.in","r",stdin);
freopen("fz.out","w",stdout);
n = read();
for(int i = 1; i <= n; ++i)a[i] = read();
t.built(1, 1, n);
int Q = read();
for(int i = 1; i <= Q; ++i){
q[i].l = read(); q[i].r = read(); q[i].id = i;
}
sort(q + 1, q + Q + 1);
int pq = 1;
for(int i = n; i >= 1; --i){
while(top && a[sta[top]] <= a[i])pop(i);
push(i);
while(pq <= Q && q[pq].l >= i){
ans[q[pq].id] = t.query(1, 1, n, q[pq].l, q[pq].r);
++pq;
}
}
for(int i = 1; i <= Q; ++i)printf("%lld\n",ans[i]);
return 0;
}
C. 旅行
暴力连边优化,在点分治时候连边,对每个深度开一个虚点
详细看学长的博客吧
https://www.cnblogs.com/MaxQAQ/p/16010035.html
题解做法是建立点分树,不过跟这个本质类似
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, int> pli;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 2e5 + 55;
const ll inf = 0x3f3f3f3f3f3f3f3f;
int n, m, cnt, rem[maxn];
struct DSU{
int f[maxn];
void init(){for(int i = 1; i <= n; ++i)f[i] = i;}
int fa(int x){return f[x] == x ? x : f[x] = fa(f[x]);}
bool merge(int x, int y){x = fa(x); y = fa(y); if(x == y)return false; f[y] = x; return true;}
}s;
int d[maxn], c[maxn];
struct EDGE{int x, y;}E[maxn];
vector<int>g[maxn];
bool del[maxn], vis[maxn * 150], in[maxn];
int dis[maxn * 150];
ll ans[maxn * 150];
priority_queue<pli, vector<pli>, greater<pli>>q;
struct edge{int to, net, val;}e[maxn * 150];
int head[maxn * 40], tot;
void add(int u, int v, int w){
e[++tot].net = head[u];
head[u] = tot;
e[tot].to = v;
e[tot].val = w;
}
int S, mx[maxn], si[maxn], root, mxd, dep[maxn];
void getroot(int x, int fa){
si[x] = 1; mx[x] = 0;
for(int v : g[x])if(!del[v] && v != fa){
getroot(v, x);
si[x] += si[v];
mx[x] = max(mx[x], si[v]);
}
mx[x] = max(mx[x], S - si[x]);
if(mx[x] < mx[root])root = x;
}
void dfs1(int x, int fa){
mxd = max(mxd, dep[x]);
for(int v : g[x])if(!del[v] && v != fa){
dep[v] = dep[x] + 1;
dfs1(v, x);
}
}
void dfs2(int x, int fa){
add(rem[dep[x]], x, 0);
if(d[x] >= dep[x])add(x, rem[min(mxd, d[x] - dep[x])], c[x]);
for(auto v : g[x])if(!del[v] && v != fa)dfs2(v, x);
}
void calc(int x){
mxd = 0;
dep[x] = 0; dfs1(x, 0);
for(int i = 0; i <= mxd; ++i)rem[i] = ++cnt;
for(int i = 1; i <= mxd; ++i)add(rem[i], rem[i - 1], 0);
dfs2(x, 0);
}
void solve(int x){
del[x] = 1; calc(x);
for(int v : g[x])if(!del[v]){
S = si[v]; root = 0;
getroot(v, x); solve(root);
}
}
void bfs(int S){
queue<int>q;
for(int i = 1; i <= n; ++i)dis[i] = 0x3f3f3f3f; dis[S] = 0; q.push(S);
while(!q.empty()){
int x = q.front(); q.pop();
for(int v : g[x])if(dis[v] > dis[x] + 1){
dis[v] = dis[x] + 1;
q.push(v);
}
}
}
int main(){
freopen("travel.in","r",stdin);
freopen("travel.out","w",stdout);
n = read(), m = read(); s.init();
for(int i = 1; i <= m; ++i)E[i].x = read(), E[i].y = read();
for(int i = 1; i <= n; ++i)d[i] = read(), c[i] = read();
for(int i = 1; i <= m; ++i)if(s.merge(E[i].x, E[i].y)){
in[i] = true; g[E[i].x].push_back(E[i].y); g[E[i].y].push_back(E[i].x);
}
cnt = S = n; mx[0] = n + n; getroot(1, 0); solve(root);
for(int i = 1; i <= m; ++i)if(!in[i]){
g[E[i].x].push_back(E[i].y);
g[E[i].y].push_back(E[i].x);
}
for(int i = 1; i <= m; ++i)if(!in[i]){
bfs(E[i].x); int mxd = 0;
for(int j = 1; j <= n; ++j)mxd = max(mxd, dis[j]);
for(int j = 0; j <= mxd; ++j)rem[j] = ++cnt;
for(int j = 1; j <= n; ++j)add(rem[dis[j]], j, 0);
for(int j = 1; j <= mxd; ++j)add(rem[j], rem[j - 1], 0);
for(int j = 1; j <= n; ++j)if(d[j] >= dis[j])add(j, rem[min(d[j] - dis[j], mxd)], c[j]);
}
for(int i = 1; i <= cnt; ++i)ans[i] = inf; q.push(pli(0, 1)); ans[1] = 0;
while(!q.empty()){
int x = q.top().second; q.pop();
if(vis[x])continue;
vis[x] = true;
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(ans[v] > ans[x] + e[i].val){
ans[v] = ans[x] + e[i].val;
q.push(pli{ans[v], v});
}
}
}
for(int i = 2; i <= n; ++i)printf("%lld\n",ans[i]);
return 0;
}
省选模拟之辞旧迎新2
A. 小 F 与游戏
阿巴阿巴
code
#include<bits/stdc++.h>
using namespace std;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 1e6 + 55, mx = 1e6;
int n, k, mod, fac[maxn], ifac[maxn];
int qpow(int x, int y){
int ans = 1;
for(; y; y >>= 1, x = 1ll * x * x % mod)if(y & 1)ans = 1ll * ans * x % mod;
return ans;
}
inline int c(int n,int m){return 1ll * fac[n] * ifac[m] % mod * ifac[n - m] % mod;}
signed main(){
freopen("game.in","r",stdin);
freopen("game.out","w",stdout);
n = read(); k = read(); mod = read();
fac[0] = ifac[0] = 1; for(int i = 1; i <= mx; ++i)fac[i] = 1ll * fac[i - 1] * i % mod;
ifac[mx] = qpow(fac[mx], mod - 2);
for(int i = mx - 1; i >= 1; --i)ifac[i] = 1ll * ifac[i + 1] * (i + 1) % mod;
if(k == 1){
printf("%d\n", qpow(2,n - 2));
return 0;
}
if(n==k){
printf("%d\n",(c(n + n - 2, n - 1) - c(n + n - 2, n - 2) + mod) % mod);
return 0;
}
printf("%d\n",1ll * qpow(2, n - k - 1) * ( c(n + k - 2, k - 1) - c(n + k - 2, k - 2) + mod) % mod);
return 0;
}
B. 小 Z 与函数
不考虑 \(vs\), 剩下的就是顺序对
现在考虑如何得到 \(vs\)
考虑执行完 \(i - 1\) 轮之后
第 \(i\) 个位置上是 \([1, i]\) 的最小值,而此次循环首次产生贡献的位置是后面第一个比最小值大的数
把贡献放到那个位置即可
但是可能会有重复选择同一个位置的情况,那么记录对于每个最小值上次选择的位置在哪里,作为查询的左界即可
code
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cassert>
#include<cstring>
#include<complex>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#define int long long
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 600005;
int n, b[maxn];
struct BIT{
int t[maxn];
int lowbit(int x){return x & -x;}
void add(int x){
while(x <= n){
++t[x];
x += lowbit(x);
}
}
int query(int x){
int ans = 0;
while(x){
ans += t[x];
x -= lowbit(x);
}
return ans;
}
void clear(){
for(int i = 1; i <= n; ++i)t[i] = 0;
}
}t;
struct seg{
int t[maxn << 2 | 1];
void build(int x, int l, int r){
if(l == r){
t[x] = b[l];
return;
}
int mid = (l + r) >> 1;
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
t[x] = max(t[x << 1], t[x << 1 | 1]);
}
int query(int x, int l, int r, int L, int R, int val){
if(t[x] <= val)return n + 1;
if(l == r)return l;
int mid = (l + r) >> 1;
if(L <= l && r <= R){
if(t[x << 1] > val)return query(x << 1, l, mid, L, R, val);
return query(x << 1 | 1, mid + 1, r, L, R, val);
}
int res = n + 1;
if(L <= mid && t[x << 1] > val)res = query(x << 1, l, mid, L, R, val);
if(res == n + 1 && R > mid && t[x << 1 | 1] > val)res = query(x << 1 | 1, mid + 1, r, L, R, val);
return res;
}
}T;
int las[maxn], cnt[maxn];
void solve(){
n = read();
for(int i = 1; i <= n; ++i)b[i] = read();
ll ans = 0; int mi = 0x3f3f3f3f;
T.build(1, 1, n);
for(int i = 1; i <= n; ++i){
ans += t.query(b[i] - 1);
ans += cnt[i];
mi = min(mi, b[i]);
int pos = max(i, las[mi]) + 1;
if(pos <= n){pos = T.query(1, 1, n, pos, n, mi); ++cnt[pos];}
las[mi] = pos;
if(t.query(b[i]) == t.query(b[i] - 1))t.add(b[i]);
printf("%lld ",ans);
}
printf("\n");
for(int i = 1; i <= n + 5; ++i)las[i] = cnt[i] = 0;
t.clear();
}
signed main(){
freopen("function.in","r",stdin);
freopen("function.out","w",stdout);
int t = read();
for(int i = 1; i <= t; ++i)solve();
return 0;
}
C. 小 W 与骑士
如果平行,坐标压成一维搞
不平行,根据平面向量基本定理得到唯一解
然后用组合数算方案数,对障碍点进行容斥,减去其他障碍点到自己的方案
https://www.cnblogs.com/MaxQAQ/p/16051258.html
code
#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cassert>
#include<cstring>
#include<complex>
#include<iostream>
#include<algorithm>
#include<unordered_map>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0;bool f = 0; char c = getchar();
while(!isdigit(c)){f = c == '-'; c = getchar();}
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return f ? -x : x;
}
const int mx = 1e6, mod = 1e9 + 7, maxn = 1e6 + 55;
int qpow(int x, int y){
int ans = 1;
for(; y; y >>= 1, x = 1ll * x * x % mod)if(y & 1)ans = 1ll * ans * x % mod;
return ans;
}
int fac[maxn], ifac[maxn];
int c(int n, int m){return 1ll * fac[n] * ifac[m] % mod * ifac[n - m] % mod;}
int f[2005], f1[2005];
bool vis[2005], flag[2005];
int x, y, k, ax, ay, bx, by;
struct node{int x, y;}d[maxn];
int calc(int x, int y){
int p, q;
q = (1ll * ax * y - 1ll * ay * x) / (1ll * ax * by - 1ll * bx * ay);
if(1ll * q * (1ll * ax * by - 1ll * bx * ay) != (1ll * ax * y - 1ll * ay * x))return 0;
p = (x - q * bx) / ax;
if(p * ax != x - q * bx || p < 0 || q < 0) return 0;
return c(p + q, p);
}
int dfs(int x){
if(vis[x])return f[x];
vis[x] = 1;
int res = calc(d[x].x, d[x].y);
if(res == 0)return f[x] = 0;
for(int i = 1; i <= k; ++i)if(i != x){
int nx = d[x].x - d[i].x;
int ny = d[x].y - d[i].y;
int v = calc(nx, ny);
if(v == 0)continue;
res = (res - 1ll * v * dfs(i) % mod + mod) % mod;
}
return f[x] = res;
}
void px(){
memset(flag,0,sizeof(flag));memset(f1,0,sizeof(f1));
if(ax * bx < 0){
printf("-1\n");
return;
}
if(ax < 0){
x = -x, y = -y, ax = -ax,ay = -ay, bx = -bx, by = -by;
for(int i = 1; i <= k; ++i)
d[i].x = -d[i].x, d[i].y = -d[i].y;
}
for(int i = 1; i < k; ++i)if(d[i].x > 0){
if(1ll * ay * d[i].x == 1ll * d[i].y * ax)flag[d[i].x] = 1;
}
f1[0] = 1;
for(int i = 0; i <= x; ++i)if(!flag[i]){
f1[i + ax] = (f1[i + ax] + f1[i]) % mod;
if(ax != bx)f1[i + bx] = (f1[i + bx] + f1[i]) % mod;
}
printf("%d\n",f1[x]);
}
void solve(){
x = read(), y = read(), k = read();
ax = read(); ay = read(); bx = read(); by = read();
for(int i = 1; i <= k; ++i)d[i].x = read(), d[i].y = read();
d[++k] = {x, y};
if(ax == 0 && ay){
swap(ax, ay); swap(bx, by); swap(x, y);
for(int i = 1; i <= k; ++i)swap(d[i].x, d[i].y);
}
if(1ll * ay * bx == 1ll * by * ax){
if(1ll * y * ax == 1ll * ay * x)px();
else printf("0\n");
return;
}
memset(f,0,sizeof(f));
memset(vis,0,sizeof(vis));
printf("%d\n",dfs(k));
}
int main(){
freopen("knight.in","r",stdin);
freopen("knight.out","w",stdout);
fac[0] = ifac[0] = 1; for(int i = 1; i <=mx; ++i)fac[i] = 1ll * fac[i - 1] * i % mod;
ifac[mx] = qpow(fac[mx], mod - 2); for(int i = mx - 1; i > 0; --i)ifac[i] = 1ll * ifac[i + 1] * (i + 1) % mod;
int t = read(); for(int i = 1; i <= t; ++i)solve();
return 0;
}
省选模拟之辞旧迎新3
A. 异或矩阵
通过观察性质发现某一位的值是他向上 \(2^x\) 行开始的 \(2^x\) 项的异或
那么得到那一行,前缀异或可以快速得到当前行
发现这个过程可以递归,次数类似快速幂
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
uint read(){
uint x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 3e6 + 5;
uint n, k, a[maxn], tmp[maxn], ans;
void sol(int k){
if(k == 1)return;
int h = 1; while(h + h <= k)h += h;
int l = k - h + 1; sol(l);
for(int i = 1; i <= n - l + 1; ++i)a[i] ^= a[i - 1];
for(int i = 1; i <= n - k + 1; ++i)tmp[i] = a[i - 1] ^ a[i + h - 1];
for(int i = 1; i <= n - k + 1; ++i)a[i] = tmp[i];
}
int main(){
freopen("matrix.in","r",stdin);
freopen("matrix.out","w",stdout);
n = read(), k = read(); a[1] = read();
for(int i = 2; i <= n; ++i)a[i] = (1145141 * a[i - 1] + 1919 * i + 810);
sol(k);
uint ans = 0;
for(int i = 1; i <= n - k + 1; ++i){
ans = (ans + i * (i ^ a[i]));
}
printf("%u\n",ans);
return 0;
}
B. 树
简单容斥题,考场傻逼了,写的相对复杂一些
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 3e5 + 55, mod = 998244353;
int n, si[maxn], p2[maxn], ans[maxn];
vector<int>g[maxn];
void add(int &x, int y){x += y; if(x >= mod)x -= mod;}
void dfs(int x, int fa){
si[x] = 1;
for(int v : g[x])if(v != fa){
dfs(v, x); si[x] += si[v];
}
int sum = si[x];
for(int v : g[x])if(v != fa){
sum -= si[v];
add(ans[x], 1ll * (p2[si[v]] - 1) * (p2[sum] - 1) % mod);
}
add(ans[x], 1);
}
int main(){
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
n = read();
for(int i = 1; i < n; ++i){
int u = read(), v = read();
g[u].push_back(v);
g[v].push_back(u);
}
p2[0] = 1; for(int i = 1; i <= n; ++i)p2[i] = (p2[i - 1] + p2[i - 1]) % mod;
dfs(1, 0);
for(int i = 1; i <= n; ++i)printf("%d\n",(ans[i] % mod + mod) % mod);
return 0;
}
C. 黑白树
因为有链加子树加这些,考虑使用树剖
那么问题在于如何维护同色连通块
发现对于在同一同色连通块内的点,他们的异色祖先数量相同
于是在线段树的每个区间都维护与区间内所有点 \(lca\) 异色祖先数量相同的信息
于是在进行 \(2 / 3\) 操作时找到当前连通块深度最小的点,对他对应的区间进行修改与查询
具体的维护 \(cnt[2], ctag[2], mx[2], mtag[2], tag\) 表示区间 \(lca\) 两种颜色祖先数量及标记,与区间 \(lca\) 在同一连通块内的点的最大值及标记,区间加标记
特殊标记只对同一连通块内的区间下传
参考博客
https://www.cnblogs.com/siriehn-nx/p/16061623.html
code
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
int read(){
int x = 0; bool f = 0; char c = getchar();
while(!isdigit(c)){f = c == '-'; c = getchar();}
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return f ? -x : x;
}
const int maxn = 200005, inf = 0x3f3f3f3f;
int n, m, col[maxn], val[maxn];
vector<int>g[maxn];
int fa[maxn], dep[maxn], si[maxn], son[maxn], dfn[maxn], dfnr[maxn], top[maxn], id[maxn], tim;
struct seg{
struct node{int cnt[2], ctag[2], mx[2], mtag[2], tag;}t[maxn << 2 | 1];
void add_cnt(int x, int col, int val){t[x].cnt[col] += val; t[x].ctag[col] += val;}
void add_mx(int x, int col, int val){t[x].mx[col] += val; t[x].mtag[col] += val;}
void add_all(int x, int val){t[x].mx[0] += val; t[x].mx[1] += val; t[x].tag += val;}
void push_up(int x){
t[x].mx[0] = max(t[x << 1].cnt[1] == t[x].cnt[1] ? t[x << 1].mx[0] : -inf, t[x << 1 | 1].cnt[1] == t[x].cnt[1] ? t[x << 1 | 1].mx[0] : -inf);
t[x].mx[1] = max(t[x << 1].cnt[0] == t[x].cnt[0] ? t[x << 1].mx[1] : -inf, t[x << 1 | 1].cnt[0] == t[x].cnt[0] ? t[x << 1 | 1].mx[1] : -inf);
}
void push_down(int x){
int ls = x << 1, rs = x << 1 | 1;
for(int i = 0; i < 2; ++i){
if(t[x].ctag[i]){add_cnt(ls, i, t[x].ctag[i]); add_cnt(rs, i, t[x].ctag[i]); t[x].ctag[i] = 0;}
if(t[x].mtag[i ^ 1]){
if(t[ls].cnt[i] == t[x].cnt[i])add_mx(ls, i ^ 1, t[x].mtag[i ^ 1]);
if(t[rs].cnt[i] == t[x].cnt[i])add_mx(rs, i ^ 1, t[x].mtag[i ^ 1]);
t[x].mtag[i ^ 1] = 0;
}
}
if(t[x].tag){add_all(ls, t[x].tag); add_all(rs, t[x].tag); t[x].tag = 0;}
}
void rev(int x, int l, int r, int pos){
if(l == r){swap(t[x].mx[0], t[x].mx[1]); return;}
push_down(x); int mid = (l + r) >> 1;
if(pos <= mid)rev(x << 1, l, mid, pos);
else rev(x << 1 | 1, mid + 1, r, pos);
push_up(x);
}
void modify_all(int x, int l, int r, int L, int R, int val){
if(L <= l && r <= R)return add_all(x, val);
push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify_all(x << 1, l, mid, L, R, val);
if(R > mid)modify_all(x << 1 | 1, mid + 1, r, L, R, val);
push_up(x);
}
void modify_cnt(int x, int l, int r, int L, int R, int col, int val){
if(L <= l && r <= R)return add_cnt(x, col, val);
push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify_cnt(x << 1, l, mid, L, R, col, val);
if(R > mid)modify_cnt(x << 1 | 1, mid + 1, r, L, R, col, val);
push_up(x);
}
void modify_mx(int x, int l, int r, int L, int R, int col, int cnt, int val){
if(t[x].cnt[col ^ 1] > cnt)return;
if(L <= l && r <= R)return add_mx(x, col, val);
push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify_mx(x << 1, l, mid, L, R, col, cnt, val);
if(R > mid)modify_mx(x << 1 | 1, mid + 1, r, L, R, col, cnt, val);
push_up(x);
}
int query_mx(int x, int l, int r, int L, int R, int col, int cnt){
if(t[x].cnt[col ^ 1] > cnt)return -inf;
if(L <= l && r <= R)return t[x].mx[col];
push_down(x); int mid = (l + r) >> 1, ans = -inf;
if(L <= mid)ans = max(ans, query_mx(x << 1, l, mid, L, R, col, cnt));
if(R > mid)ans = max(ans, query_mx(x << 1 | 1, mid + 1, r, L, R, col, cnt));
return ans;
}
int query_cnt(int x, int l, int r, int pos, int col){
if(l == r)return t[x].cnt[col];
push_down(x); int mid = (l + r) >> 1;
if(pos <= mid)return query_cnt(x << 1, l, mid, pos, col);
else return query_cnt(x << 1 | 1, mid + 1, r, pos, col);
}
}T;
void dfs1(int x){
si[x] = 1;
for(int v : g[x])if(v != fa[x]){
fa[v] = x; dep[v] = dep[x] + 1;
dfs1(v); si[x] += si[v];
if(si[son[x]] < si[v])son[x] = v;
}
}
set<pii>s[2][maxn];
void dfs2(int x, int tp){
id[dfn[x] = ++tim] = x; top[x] = tp;
if(son[x])dfs2(son[x], tp);
for(int v : g[x])if(v != fa[x] && v != son[x])dfs2(v, v);
dfnr[x] = tim;
}
int find(int x){
pii res; res.first = dep[x]; res.second = x; int c = !col[x];
for(; x; x = fa[top[x]]){
auto it = s[c][top[x]].upper_bound({dep[x], inf});
if(it != s[c][top[x]].begin()){
--it;
if((*it).first + 1 < res.first)res = {1 + (*it).first, son[(*it).second]};
break;
}
res = {dep[top[x]], top[x]};
}
return res.second;
}
void upd(int u, int v, int val){
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]])swap(u, v);
T.modify_all(1, 1, n, dfn[top[u]], dfn[u], val);
u = fa[top[u]];
}
if(dep[u] > dep[v])swap(u, v);
T.modify_all(1, 1, n, dfn[u], dfn[v], val);
}
int main(){
freopen("astill.in","r",stdin);
freopen("astill.out","w",stdout);
n = read(), m = read();
for(int i = 1; i < n; ++i){
int u = read(), v = read();
g[u].push_back(v); g[v].push_back(u);
}
for(int i = 1; i <= n; ++i)col[i] = read();
for(int i = 1; i <= n; ++i)val[i] = read();
dfs1(1); dfs2(1, 1);
for(int i = 1; i <= n; ++i)s[col[i]][top[i]].insert({dep[i], i});
for(int i = 1; i <= n; ++i)T.modify_cnt(1, 1, n, dfn[i], dfnr[i], col[i], 1);
for(int i = 1; i <= n; ++i)T.modify_all(1, 1, n, dfn[i], dfn[i], val[i]);
for(int i = 1; i <= m; ++i){
int opt = read(), x = read();
if(opt == 1){
T.modify_cnt(1, 1, n, dfn[x], dfnr[x], col[x], -1);
s[col[x]][top[x]].erase({dep[x], x});
col[x] ^= 1;
s[col[x]][top[x]].insert({dep[x], x});
T.rev(1, 1, n, dfn[x]);
T.modify_cnt(1, 1, n, dfn[x], dfnr[x], col[x], 1);
}else if(opt == 2){
x = find(x);
T.modify_mx(1, 1, n, dfn[x], dfnr[x], col[x], T.query_cnt(1, 1, n, dfn[x], !col[x]), read());
}else if(opt == 3){
x = find(x);
printf("%d\n",T.query_mx(1, 1, n, dfn[x], dfnr[x], col[x], T.query_cnt(1, 1, n, dfn[x], !col[x])));
}else if(opt == 4){int y = read(); upd(x, y, read());
}else T.modify_all(1, 1, n, dfn[x], dfnr[x], read());
}
return 0;
}
省选模拟之辞旧迎新4
A. 逃离藏宝洞
随机走一边,查询,不对就退回去
错误两次就能确定正确方向,此时直接走上去
询问次数远小于步数的随机一次走 \(50\) 步左右,期望下正确
code
#include"escape.h"
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
mt19937 rd((ull)(new char) * (ull)(new char));
int sint(int l, int r){return uniform_int_distribution<>(l, r)(rd);}
int rdr(int from){
int t = sint(0, 2);
while(t == from)t = sint(0, 2);
return t;
}
int res(int x, int y){
if(x > y)swap(x, y);
if(x)return 0;
if(y == 2)return 1;
return 2;
}
void know1(int dep, int from){
int t1 = rdr(from), d1;
move(t1); d1 = query();
if(d1 == dep - 1){
move(t1);
move(t1 = res(from, t1));
}
know1(dep + 1, t1);
}
void solve1(){
int dep, ndep, tt = rdr(-1);
dep = query();
move(tt);
ndep = query();
if(ndep == dep - 1)move(tt), know1(dep, tt);
else know1(dep + 1, tt);
}
int l[100005], lim;
void move50(int from){
l[0] = from;
for(int i = 1; i <= lim; ++i)l[i] = rdr(l[i - 1]);
for(int i = 1; i <= lim; ++i)move(l[i]);
}
void ret(int x){
for(int i = lim; i > x; --i)move(l[i]);
}
void know1_50(int dep, int from){
int ndep;
move50(from);
ndep = query();
int cro = (lim - (dep - ndep)) / 2;
ret(cro);
if(cro == 50)know1_50(dep + 1, l[50]);
if(cro == 0){
move(res(from, l[1]));
know1_50(dep + 1, res(from, l[1]));
}else{
dep = dep + cro;
move(res(l[cro], l[cro + 1]));
know1_50(dep + 1, res(l[cro], l[cro + 1]));
}
}
void solve2(){
int dep, ndep; dep = query();
move50(-1); ndep = query();
int cro = (lim - (dep - ndep)) / 2;
ret(cro);
dep = dep + cro;
know1_50(dep, l[cro]);
}
void escape(int lm, int lq){
lim = 50;
if(lm == 1e7 && lq != 100002)solve2();
else solve1();
}
B. 序列划分
首先 \(DP\) 枚举最后一段
\(f_i = \sum _{j < i} f_j mex_{j, i}\)
套路的用线段树维护 \(mex\)
转换 \(DP\) 为刷表法
\(f_i mex_{i, j}-> [j > i] f_j\)
那么我们有区间覆盖和区间乘对应项两种操作,
首先确定一个顺序,由于区间覆盖会影响对应项,于是他后做
那么考虑如何合并标记,当区间乘发现该区间覆盖过,其实可以转换成加上定值
于是新维护一个加法标记即可
初始化令叶结点区间覆盖标记存在,那么下传标记就不用特判了
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c)) c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 1e6 + 55, mod = 998244353;
int n, a[maxn], mex[maxn], nxt[maxn], pos[maxn];
int f[maxn];
bool vis[maxn];
void add(int &x, int y){x += y; if(x >= mod) x -= mod;}
struct seg{
struct node{
int val, mex, mul, tag;
}t[maxn << 2 | 1];
void push_up(int x){t[x].mex = max(t[x << 1].mex, t[x << 1 | 1].mex);}
void push_down(int x){
int ls = x << 1, rs = x << 1 | 1;
if(t[x].mul){
if(t[ls].tag != -1)add(t[ls].val, 1ll * t[x].mul * t[ls].tag % mod);
else add(t[ls].mul, t[x].mul);
if(t[rs].tag != -1)add(t[rs].val, 1ll * t[x].mul * t[rs].tag % mod);
else add(t[rs].mul, t[x].mul);
t[x].mul = 0;
}
if(t[x].val){
add(t[ls].val, t[x].val);
add(t[rs].val, t[x].val);
t[x].val = 0;
}
if(t[x].tag != -1){
t[ls].tag = t[rs].tag = t[x].tag;
t[ls].mex = t[rs].mex = t[x].tag;
t[x].tag = -1;
}
}
void build(int x, int l, int r){
t[x].tag = -1;
if(l == r){t[x].mex = t[x].tag = mex[l]; return;}
int mid = (l + r) >> 1;
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
push_up(x);
}
void modify_val(int x, int l, int r, int L, int R, int val){
if(L <= l && r <= R){
if(t[x].tag != -1) add(t[x].val, 1ll * t[x].tag * val % mod);
else add(t[x].mul, val);
return;
}
push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify_val(x << 1, l, mid, L, R, val);
if(R > mid)modify_val(x << 1 | 1, mid + 1, r, L, R, val);
}
void modify_mex(int x, int l, int r, int L, int R, int mex){
if(L <= l && r <= R){
t[x].mex = t[x].tag = mex;
return;
}
push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify_mex(x << 1, l, mid, L, R, mex);
if(R > mid)modify_mex(x << 1 | 1, mid + 1, r, L, R, mex);
push_up(x);
}
int find(int x, int l, int r, int val){
if(l == r)return l + (t[x].mex <= val);
push_down(x); int mid = (l + r) >> 1;
if(t[x << 1].mex > val)return find(x << 1, l, mid, val);
else return find(x << 1 | 1, mid + 1, r, val);
}
int query(int x, int l, int r, int pos){
if(l == r)return t[x].val;
push_down(x); int mid = (l + r) >> 1;
if(pos <= mid)return query(x << 1, l, mid, pos);
else return query(x << 1 | 1, mid + 1, r, pos);
}
}T;
int main(){
freopen("divide.in","r",stdin);
freopen("divide.out","w",stdout);
n = read(); for(int i = 1; i <= n; ++i)a[i] = read();
for(int i = 0; i <= n; ++i)pos[i] = n + 1;
for(int i = n; i >= 1; --i)if(a[i] <= n){
nxt[i] = pos[a[i]]; pos[a[i]] = i;
}
for(int i = 1; i <= n; ++i){
mex[i] = mex[i - 1];
if(a[i] <= n){
vis[a[i]] = true;
while(vis[mex[i]])++mex[i];
}
}
T.build(1, 1, n); T.modify_val(1, 1, n, 1, n, 1);
for(int i = 1; i < n; ++i){
if(a[i] <= n){
int pl = T.find(1, 1, n, a[i]);
if(pl < nxt[i])T.modify_mex(1, 1, n, pl, nxt[i] - 1, a[i]);
}
T.modify_val(1, 1, n, i + 1, n, T.query(1, 1, n, i));
}
printf("%d\n",T.query(1, 1, n, n));
return 0;
}
C. 重排列
https://www.luogu.com.cn/problem/AT_agc010_e
把不互质的两个数连边,形成一个图
操作的实质是先手对图定向,后手进行字典序最大的拓扑排序
那么先手的最优策略就是对每个连通块定向时,贪心的从最小点开始,按照顺序扫描边,优先走字典序小的边
后手策略就是用大根堆进行拓扑排序
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c)) c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 2005;
bool vis[maxn];
int n, a[maxn], deg[maxn];
vector<int>g[maxn];
priority_queue<int>q;
void dfs(int x){
vis[x] = true;
for(int i = 1; i <= n; ++i)
if(!vis[i] && __gcd(a[i], a[x]) != 1){
++deg[i]; g[x].push_back(i); dfs(i);
}
}
int main(){
freopen("permutation.in","r",stdin);
freopen("permutation.out","w",stdout);
n = read(); for(int i = 1; i <= n; ++i)a[i] = read();
sort(a + 1, a + n + 1);
for(int i = 1; i <= n; ++i)if(!vis[i])dfs(i);
for(int i = 1; i <= n; ++i)if(deg[i] == 0)q.push(i);
while(!q.empty()){
int x = q.top(); q.pop();
printf("%d ",a[x]);
for(int v : g[x])q.push(v);
}
return 0;
}
省选模拟之辞旧迎新5
A. 交通
发现如果能快速找到从当前时刻和位置到下一个红灯的位置,那么之后的行为就是确定的
设 \(f_x\) 表示从 \(x\) 绿灯 \(0S\) 开始到终点的时间
如何查找,我们需要找一个后缀中,取值在一个区间里最靠前的位置
好像是二维数点?
其实倒着扫就行了,对于取值的限制在线段树上维护 \(mod (g + r)\) 意义下的值
单点修改区间查询或者像我一样\(SB\) 的区间修改单点查询也行
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 5e4 + 55;
int n, g, r, q, mod;
struct seg{
struct node{
int l, r, v;
}t[maxn * 80];
int cnt, root;
void modify(int &x, int l, int r, int L, int R, int pos){
if(!x)t[x = ++cnt].v = maxn;
if(L <= l && r <= R){t[x].v = pos; return;}
int mid = (l + r) >> 1;
if(L <= mid)modify(t[x].l, l, mid, L, R, pos);
if(R > mid)modify(t[x].r, mid + 1, r, L, R, pos);
}
int query(int x, int l, int r, int pos){
if(!x)return maxn;
if(l == r)return t[x].v;
int mid = (l + r) >> 1;
if(pos <= mid)return min(t[x].v, query(t[x].l, l, mid, pos));
else return min(t[x].v, query(t[x].r, mid + 1, r, pos));
}
}T;
ll f[maxn], d[maxn];
void upd(int x, int pos){
if(x < g)T.modify(T.root, 0, mod - 1, x + 1, x - g + mod, pos);
else{
T.modify(T.root, 0, mod - 1, 0, x - g, pos);
T.modify(T.root, 0, mod - 1, x + 1, mod - 1, pos);
}
}
int main(){
freopen("traffic.in","r",stdin);
freopen("traffic.out","w",stdout);
n = read() + 1, g = read(), r = read(); mod = g + r;
for(int i = 1; i <= n; ++i)d[i] = read();
for(int i = 1; i <= n; ++i)d[i] += d[i - 1];
q = read(); T.modify(T.root, 0, mod - 1, 0, mod - 1, n + 1);
for(int i = n; i >= 2; --i){
int pos = T.query(T.root, 0, mod - 1, d[i - 1] % mod);
if(pos == n + 1)f[i] = d[n] - d[i - 1];
else f[i] = d[pos - 1] - d[i - 1] + f[pos] + (mod - (d[pos - 1] - d[i - 1]) % mod) % mod;
upd(d[i - 1] % mod, i);
}
for(int i = 1; i <= q; ++i){
ll ans = read();
int pos = T.query(T.root, 0, mod - 1, (mod - ans % mod) % mod);
if(pos == n + 1)ans = ans + d[n];
else ans = ans + d[pos - 1] + f[pos] + mod - (d[pos - 1] + ans) % mod;
printf("%lld\n",ans);
}
return 0;
}
B. 选拔
设 \(f_{x, i} g_{x, i}\) 分别表示树上 \(x\) 向下匹配一段前缀/后缀是否合法
把所有串拼起来中间加特殊字符
然后用 \(bitset\) 进行优化
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int maxn = 60005;
int n, m, id[maxn], tim, fa[maxn];
vector<pii>e[maxn];
string s, t[maxn];
bitset<maxn>b[27], f[maxn], g[maxn], ans;
void dfs(int x){
id[++tim] = x;
for(auto v : e[x])if(v.first != fa[x]){
fa[v.first] = x; dfs(v.first);
}
}
int main(){
freopen("selection.in","r",stdin);
freopen("selection.out","w",stdout);
cin >> n;
for(int i = 1; i < n; ++i){
int u, v; cin >> u >> v >> s;
e[u].push_back(pii(v, s[0] - 'a'));
e[v].push_back(pii(u, s[0] - 'a'));
}
cin >> m; s = "";
for(int i = 1; i <= m; ++i){
cin >> t[i];
s += char('z' + 1) + t[i];
}
s += char('z' + 1);
int len = s.size();
for(int i = 0; i < len; ++i)b[s[i] - 'a'][i] = 1;
dfs(1);
for(int i = n; i >= 1; --i){
int x = id[i]; f[x] = g[x] = b[26];
for(auto v : e[x])if(v.first != fa[x]){
f[v.first] = (f[v.first] << 1) & b[v.second];
g[v.first] = (g[v.first] >> 1) & b[v.second];
ans = ans | ((f[x] << 1) & g[v.first]);
ans = ans | (g[x] & (f[v.first] << 1));
f[x] |= f[v.first]; g[x] |= g[v.first];
}
}
for(int i = 1, sum = 1; i <= m; ++i){
int l = t[i].size(); bool flag = true;
for(int j = 0; j <= l; ++j){
if(ans[j + sum]){
cout << "YES" << endl;
flag = false;
break;
}
}
if(flag)cout << "NO" << endl;
sum += l + 1;
}
return 0;
}
C. 等待



https://www.cnblogs.com/apjifengc/protected/p/daily-2023-2-2.html
衡石春季赛模拟1
所以石真的是某二中
A. 签到题
https://www.cnblogs.com/Chencgy/p/16538848.html
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 1e6 + 55;
int n, m, k, c, deg[maxn];
int main(){
freopen("qiandao.in","r",stdin);
freopen("qiandao.out","w",stdout);
n = read(), m = read(), k = read(), c = read();
for(int i = 1; i <= k; ++i){
int u = read(), v = read();
++deg[u]; ++deg[n + v];
}
int ans = 0;
for(int i = 1; i <= n + m; ++i)ans += (deg[i] % c) ? 1 : 0;
printf("%d\n",ans);
return 0;
}
B. M 弟娃
树上简单容斥一下
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 3e5 + 55;
int n, m;
vector<int>g[maxn];
int si[maxn], fa[maxn][20], dep[maxn], dfn[maxn], dfnr[maxn], tim;
void dfs(int x){
dfn[x] = ++tim; si[x] = 1;
for(int v : g[x])if(v != fa[x][0]){
dep[v] = dep[x] + 1;
fa[v][0] = x;
dfs(v);
si[x] += si[v];
}
dfnr[x] = tim;
}
int kfa(int x, int k){
for(int i = 19; i >= 0; --i)if((k >> i) & 1)x = fa[x][i];
return x;
}
struct seg{
struct node{
int tag, val;
}t[maxn << 2 | 1];
void upd(int x, int val){
t[x].val += val;
t[x].tag += val;
}
void push_down(int x){
upd(x << 1, t[x].tag);
upd(x << 1 | 1, t[x].tag);
t[x].tag = 0;
}
void push_up(int x){t[x].val = max(t[x << 1].val , t[x << 1 | 1].val);}
void modify(int x, int l, int r, int L, int R, int val){
if(L <= l && r <= R)return upd(x, val);
if(t[x].tag)push_down(x); int mid = (l + r) >> 1;
if(L <= mid)modify(x << 1, l, mid, L, R, val);
if(R > mid)modify(x << 1 | 1, mid + 1, r, L, R, val);
push_up(x);
}
int query(){return t[1].val;}
}T;
int main(){
freopen("magic.in","r",stdin);
freopen("magic.out","w",stdout);
n = read(), m = read();
for(int i = 1; i < n; ++i){
int u = read(),v = read();
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1);
for(int i = 1; i <= 19; ++i)
for(int j = 1; j <= n; ++j)
fa[j][i] = fa[fa[j][i - 1]][i - 1];
for(int i = 1; i <= m; ++i){
int u = read(), v = read();
if(u == v)T.modify(1, 1, n, 1, n, 1);
else{
if(si[u] < si[v])swap(u, v);
if(dfn[u] <= dfn[v] && dfnr[v] <= dfnr[u]){
T.modify(1, 1, n, 1, n, 1);
int dec = kfa(v, dep[v] - dep[u] - 1);
T.modify(1, 1, n, dfn[dec], dfnr[dec], -1);
T.modify(1, 1, n, dfn[v], dfnr[v], 1);
}else{
T.modify(1, 1, n, dfn[u], dfnr[u], 1);
T.modify(1, 1, n, dfn[v], dfnr[v], 1);
}
}
printf("%d\n",T.query());
}
return 0;
}
C. 变异大老鼠
最短路树上 \(DP\)
注意转移开临时数组。。。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 3e4 + 55, inf = 0x3f3f3f3f;
int n, m, k, head[maxn], tot, fa[maxn];
struct edge{int to, net, val;}e[maxn << 1 | 1];
vector<int>g[maxn];
void add(int u, int v, int w){
e[++tot] = {v, head[u], w};
head[u] = tot;
}
int dis[maxn]; bool vis[maxn];
priority_queue<pii, vector<pii>, greater<pii>>q;
double p[305][305], f[305][305], tmp[305];
void dfs(int x){
for(int v : g[x]){
dfs(v);
for(int i = 0; i <= k; ++i)tmp[i] = 0;
for(int i = 0; i <= k; ++i)
for(int j = i; j <= k; ++j)
tmp[j] = max(tmp[j], f[x][i] + f[v][j - i]);
for(int i = 0; i <= k; ++i)f[x][i] = tmp[i];
}
if(g[x].size())for(int i = 1; i <= k; ++i)f[x][i] /= g[x].size();
for(int i = 1; i <= k; ++i)tmp[i] = 0;
for(int i = 1; i <= k; ++i)
for(int j = 0; j <= i; ++j)
tmp[i] = max(tmp[i], f[x][j] * (1 - p[x][i - j]) + p[x][i - j]);
for(int i = 1; i <= k; ++i)f[x][i] = tmp[i];
}
int main(){
freopen("arrest.in","r",stdin);
freopen("arrest.out","w",stdout);
n = read(), m = read(), k = read();
for(int i = 1; i <= m; ++i){
int u = read(), v = read(), w = read();
add(u, v, w); add(v, u, w);
}
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= k; ++j)
scanf("%lf",&p[i][j]);
for(int i = 2; i <= n; ++i)dis[i] = inf;
q.push(pii(0, 1));
while(!q.empty()){
int x = q.top().second; q.pop();
if(vis[x])continue; vis[x] = true;
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(dis[v] > dis[x] + e[i].val){
fa[v] = x;
dis[v] = dis[x] + e[i].val;
q.push(pii(dis[v], v));
}
}
}
for(int i = 2; i <= n; ++i)g[fa[i]].push_back(i);
dfs(1);
double ans = 0;
for(int i = 0; i <= k; ++i)ans = max(ans, f[1][i]);
printf("%.6lf\n",ans);
return 0;
}
D. 朝鲜时蔬
数据点分治
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
ll read(){
ll x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int mod = 1e9 + 7;
ll qpow(ll x, ll y){
ll ans = 1;
for(; y; y >>= 1, x = x * x % mod)if(y & 1)ans = ans * x % mod;
return ans;
}
const int inv2=500000004,inv6=166666668,inv24=41666667;
ll n, m, k;
ll calc(ll l, ll r){l %= mod; r %= mod; return (l + r) * (r - l + 1) % mod;}
ll g(ll x){x %= mod; return x * (x + 1) % mod * (2 * x + 1) % mod * qpow(6, mod - 2) % mod;}
int main(){
freopen("vegetable.in","r",stdin);
freopen("vegetable.out","w",stdout);
n = read(), m = read(), k = read();
if(m == k){
ll ans = 1;
for(int i = 1; i <= m; ++i, --n)ans = ans * (n % mod) % mod;
for(int i = 1; i <= m; ++i)ans = ans * qpow(i, mod - 2) % mod;
printf("%lld\n",ans);
return 0;
}
if(m == 2 && k == 1){
ll ans = mod - n;
for(ll l = 1, r; l <= n; l = r + 1){
r = n / (n / l);
ans += (r - l + 1) % mod * ((n / l) % mod) % mod;
ans %= mod;
}
printf("%lld\n",ans);
return 0;
}
if(m == 3 && k == 1){
printf("%lld\n",(n / 3) % mod);
return 0;
}
if(m == 3 && k == 2){
ll ans = 0;
for(ll l = 3, r; l <= n; l = r + 1){
r = n / (n / l);
ans = (ans + (n / l) % mod * calc((l - 1) / 2, (r - 1) / 2)) % mod;
if(l % 2 == 0)ans = (ans - (n / l) % mod * (((l - 1) / 2) % mod) % mod + mod) % mod;
if(r % 2 == 1)ans = (ans - (n / l) % mod * (((r - 1) / 2) % mod) % mod + mod) % mod;
}
ans = (ans % mod + mod) % mod;
printf("%lld\n",ans);
return 0;
}
if(m == 4 && k == 1){
if(n <= 5){
printf("%d\n",n >= 4);
return 0;
}
printf("%lld\n",((n / 6) + (n / 9) + (n / 10) + (n / 12) + (n / 15) + (n / 21)) % mod);
return 0;
}
if(m == 4 && k == 2){
if(n <= 6)printf("%d\n",n >= 4);
else if(n == 7)printf("3\n");
else if(n == 8)printf("6\n");
else if(n == 9)printf("9\n");
else if(n == 10)printf("10\n");
else printf("%lld\n",((n / 11) + (n / 29) ) % mod);
return 0;
}
if(m == 4 && k == 3){
if(n < 4)printf("0\n");
else if(n == 4)printf("1\n");
else if(n == 5)printf("5\n");
else{
ll ans = 0;
for(ll l = 1, r; l <= n; l = r + 1){
r = n / (n / l); ll len = (r - l + 1) % mod;
ans = (ans + (n / l) % mod * (5 * len + (g(r) - g(l - 1) + mod) % mod - 6 * (l + r) % mod * len % mod * qpow(2, mod - 2) % mod + 3 * (r / 2 - (l + 1) / 2 + 1 + mod) % mod + 4 * (r / 3 - (l + 2) / 3 + 1 + mod) % mod + mod) % mod) % mod;
}
ans = ans * qpow(12, mod - 2) % mod;
printf("%lld\n",ans);
}
}
return 0;
}
衡石春季赛模拟2
A. 魔法
正着思考比较困难,考虑倒着想,发现每次选择一个满足条件的连续段删去
简单思考发现是个栈
不过记得输出时候应该倒着输。。。。。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 2e5 + 55;
char s[maxn];
int n, r, b, top, tot, st[maxn], cr[maxn], cb[maxn];
vector<int>ans[maxn];
int main(){
freopen("magic.in","r",stdin);
freopen("magic.out","w",stdout);
scanf("%d%d%d",&n,&r,&b);
scanf("%s",s + 1);
for(int i = 1; i <= n; ++i){
st[++top] = i;
cr[top] = cr[top - 1] + (s[i] == 'R');
cb[top] = cb[top - 1] + (s[i] == 'B');
if(top >= r + b && cr[top] - cr[top - r - b] == r && cb[top] - cb[top - r - b] == b){
++tot;
for(int i = 1; i <= r + b; ++i)ans[tot].push_back(st[top--]);
}
}
if(top == 0){
printf("YES\n");
printf("%d\n",tot);
for(int i = tot; i >= 1; --i){
for(int v : ans[i])printf("%d ",v);
printf("\n");
}
}else printf("NO\n");
return 0;
}
B. 连通性
设 \([1, n - m]\) 为黑点,剩下的为白点
发现白点不能改变图中除了他本身的连通性
那么如果一个连通块只有白点,那么连通块为完全图
如果一个连通块两种点都有,那么白点必然至少连接一个黑点
如果一个连通块只有黑点,可以通过经典容斥进行计算
即
设 \(f_{n, m}\) 表示答案
初始条件 \(f_{n, 0} = 2^{\binom{n}{2}}\)
转移考虑枚举白点 \(n\) 所在的连通块
- 只有白点
黑白都有
其中
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 105, mx = 100, mod = 1e9 + 7;
int qpow(int x, int y){
int ans = 1;
for(; y; y >>= 1, x = 1ll * x * x % mod)if(y & 1)ans = 1ll * ans * x % mod;
return ans;
}
int t, n, m, p2[maxn * maxn], c[maxn][maxn];
int g[maxn], f[maxn][maxn], h[maxn][maxn];
int main(){
// freopen("floyd.in","r",stdin);
// freopen("floyd.out","w",stdout);
for(int i = 0; i <= mx; ++i){
c[i][0] = 1;
for(int j = 1; j <= i; ++j)
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
p2[0] = 1;
for(int i = 1; i <= mx * mx; ++i)
p2[i] = (p2[i - 1] + p2[i - 1]) % mod;
for(int i = 1; i <= mx; ++i){
g[i] = p2[i * (i - 1) / 2];
for(int j = 1; j <= i - 1; ++j)
g[i] = (g[i] - 1ll * g[j] * p2[(i - j) * (i - j - 1) / 2] % mod * c[i - 1][j - 1]) % mod;
g[i] = (g[i] + mod) % mod;
}
for(int i = 1; i <= mx; ++i)
for(int j = 1; j <= mx - i; ++j)
h[i][j] = 1ll * g[j] * qpow(p2[j] - 1, i) % mod * p2[i * (i - 1) / 2] % mod;
f[0][0] = 1;
for(int n = 1; n <= mx; ++n){
f[n][0] = p2[n * (n - 1) / 2];
for(int m = 1; m <= n; ++m){
for(int i = 1; i <= m; ++i)
f[n][m] = (f[n][m] + 1ll * f[n - i][m - i] * c[m - 1][i - 1]) % mod;
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n - m; ++j)
f[n][m] = (f[n][m] + 1ll * f[n - i - j][m - i] * c[m - 1][i - 1] % mod * c[n - m][j] % mod * h[i][j]) % mod;
}
}
int t = read();
for(int i = 1; i <= t; ++i){
n = read(), m = read();
printf("%d\n",f[n][m]);
}
return 0;
}
C. 字符串的价值
字符集\(14\), 那大概是状压,题目的形式非常 \(AC\) 自动机于是在自动机上 \(DP\)
暴力不太行,但是考虑决策只发生在 \(?\) 处,那么可以把没有问号的一段直接转移
就是每次转移一个结点的信息时,处理目标结点以及路径上的权值和,对不同状态一起转移
把状态按照 \(popcount\) 分开,发现转移是个 \(deg\) ,也就不用滚动数组了
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
const int maxn = 4e5 + 55, mx = 1005;
char s[maxn], c[mx];
int k, val[mx], pos[mx], n, pop[(1 << 14) + 5];
vector<int>trs[15];
struct AC{
int ch[1005][14], fail[1005], cnt = 1, root = 1, sv[1005];
int insert(){
int now = 1, l = strlen(c + 1);
for(int i = 1; i <= l; ++i){
if(!ch[now][c[i] - 'a'])ch[now][c[i] - 'a'] = ++cnt;
now = ch[now][c[i] - 'a'];
}
return now;
}
queue<int>q;
vector<int>g[1005];
void build(){
for(int i = 0; i < 14; ++i)if(ch[root][i])q.push(ch[root][i]), fail[ch[root][i]] = root;
else ch[root][i] = root;
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = 0; i < 14; ++i)
if(ch[x][i])q.push(ch[x][i]), fail[ch[x][i]] = ch[fail[x]][i];
else ch[x][i] = ch[fail[x]][i];
}
}
void dfs(int x){
for(int v : g[x]){
sv[v] += sv[x];
dfs(v);
}
}
void init(){
build();
for(int i = 2; i <= cnt; ++i)g[fail[i]].push_back(i);
for(int i = 1; i <= k; ++i)sv[pos[i]] += val[i];
dfs(1);
}
int f[1005][(1 << 14) + 5];
int solve(){
memset(f, -0x3f, sizeof(f));
f[1][0] = 0; int ans = -INT_MAX;
for(int l = 1, r = 1, tim = 1; l <= n ; l = r + 1, ++tim){
r = l;
while(r <= n && s[r] != '?')++r;
for(int i = 1; i <= cnt; ++i){
int to = i, v = 0;
for(int o = l; o < r; ++o){
to = ch[to][s[o] - 'a'];
v += sv[to];
}
for(auto s : trs[tim - 1])if(f[i][s] != f[0][0]){
if(r == n + 1){
ans = max(ans, f[i][s] + v);
continue;
}
for(int t = 0; t < 14; ++t)if(!((s >> t) & 1)){
if(r < n)f[ch[to][t]][s | (1 << t)] = max(f[ch[to][t]][s | (1 << t)], f[i][s] + v + sv[ch[to][t]]);
else ans = max(ans, f[i][s] + v + sv[ch[to][t]]);
}
}
}
}
return ans;
}
}A;
int main(){
freopen("value.in","r",stdin);
freopen("value.out","w",stdout);
scanf("%d",&k);
for(int i = 1; i <= k; ++i){
scanf("%s%d",c + 1,&val[i]);
pos[i] = A.insert();
}
scanf("%s",s + 1); n = strlen(s + 1);
for(int i = 1; i < (1 << 14); ++i){
pop[i] = pop[i >> 1] + (i & 1);
trs[pop[i]].push_back(i);
}
trs[0].push_back(0);
A.init();
printf("%d\n",A.solve());
return 0;
}
D. 排列
对题解做一点补充。
首先各段逆序对数乘积等于在每一段选出一个逆序对的方案数
现在我们已知一个划分,求出所有排列选择方案数最后除掉 \(2n!\) 就是其价值
那么我们可以枚举一段内两个位置,计算有多少排列选择这两个位置为逆序对
那么除掉 \(2n!\) 变成了选择两个位置,他们构成逆序对的概率
答案就是每段选择的位置构成逆序对概率之和
现在考虑转化一些限制方便后面的处理
对于偶数位置有序的限制,我们考虑所有排列但是只统计有有序的部分,最后乘上 \(n!\) 即可
那么我们考虑

把偶数位的限制看成边,作为树的主干,现在我们考虑一个 \(DP\)
\(f_{i, j, k}\) 表示前 \(2i\) 个位置,划分 \(j\) 段, 额外的子树大小为 \(k\) 的每一段选择两个位置为逆序对的概率之和
其中额外的子树是因为某些位置构成逆序对时需要满足与偶数链的一些相对关系
考虑枚举两个位置,分情况讨论
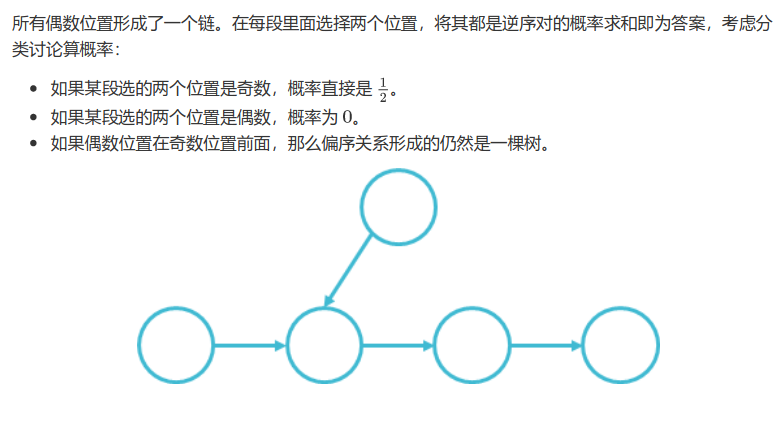
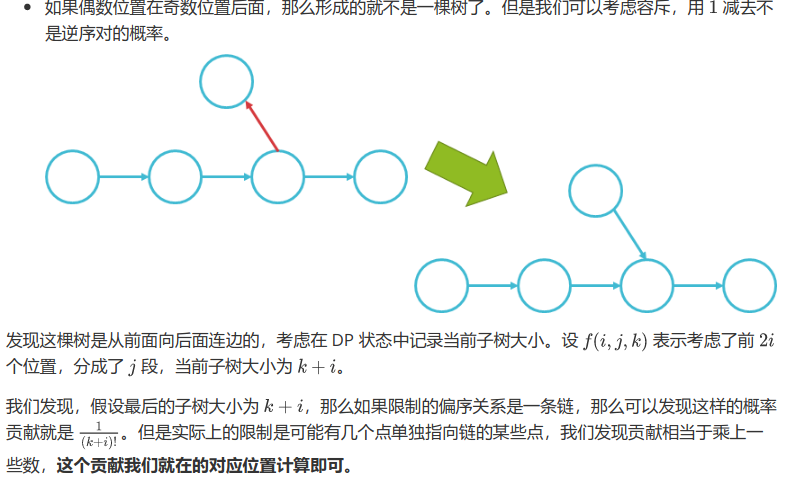
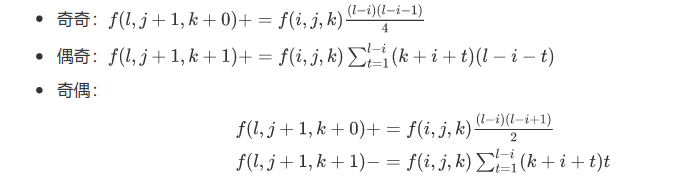
奇奇 就是在这一段选择两个奇数点的方案乘上 \(\frac{1}{2}\)
偶奇是枚举偶数的位置得到奇数位置总数,乘上把奇数放到树上而不是链上多除掉的部分
奇偶则需要枚举偶数位置计算奇数位置总数减去构成顺序对的概率
最后
感觉题解写了跟写了似的。。。
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 205, mx = 200;
int mod;
int qpow(int x, int y){
int ans = 1;
for(; y; y >>= 1, x = 1ll * x * x % mod)if(y & 1)ans = 1ll * ans * x % mod;
return ans;
}
int ans[105][105];
int fac[maxn], ifac[maxn];
int f[105][105][105], g[105][105][105][2];
void add(int &x, int y){x += y; if(x >= mod) x -= mod;}
int main(){
// freopen("permutation.in","r",stdin);
// freopen("permutation.out","w",stdout);
mod = read(); fac[0] = ifac[0] = 1;
for(int i = 1; i <= mx; ++i)fac[i] = 1ll * fac[i - 1] * i % mod;
ifac[mx] = qpow(fac[mx], mod - 2);
for(int i = mx - 1; i >= 1; --i)ifac[i] = 1ll * ifac[i + 1] * (i + 1) % mod;
int n = 100; f[0][0][0] = 1;
for(int i = 0; i <= n; ++i)
for(int k = 0; k <= i; ++k)
for(int l = i + 1; l <= n; ++l)
for(int t = 1; t <= l - i; ++t)
add(g[i][k][l][0], 1ll * (k + i + t) * (l - i - t) % mod),
add(g[i][k][l][1], 1ll * (k + i + t) * t % mod);
for(int i = 0; i <= n; ++i)
for(int j = 0; j <= i; ++j)
for(int k = 0; k <= j; ++k)
for(int l = i + 1; l <= n; ++l){
add(f[l][j + 1][k], 1ll * f[i][j][k] * (l - i) % mod * (l - i - 1) % mod * ifac[2] % mod * ifac[2] % mod);
add(f[l][j + 1][k + 1], 1ll * f[i][j][k] * g[i][k][l][0] % mod);
// add(f[l][j + 1][k], 1ll * f[i][j][k] * (l - i) % mod * (l - i + 1) % mod * ifac[2] % mod);
add(f[l][j + 1][k + 1], mod - 1ll * f[i][j][k] * g[i][k][l][1] % mod);
}
for ( int i = 1; i <= 5; i ++ )
for ( int j = 1; j <= i; j ++ )
for ( int k = 0; k <= j; k ++ )printf("%d %d %d %d\n",i, j, k, 1ll * f[i][j][k] * ifac[k + i] % mod);
fflush(stdout);
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= i; ++j)
for(int k = 0; k <= j; ++k)
add(ans[i][j], 1ll * f[i][j][k] * ifac[k + i] % mod);
int t = read();
for(int i = 1; i <= t; ++i){
int n = read(), k = read();
printf("%lld\n", 1ll * ans[n][k] * fac[n] % mod);
}
return 0;
}
省选模拟Plus1
A. 旅行计划
在一个连通块内的边可以任意走,支持在一条边那里反复横跳,所以 \(k\) 为奇数时候 \(u - > v\) 每条边走 \(k\) 次可以得到最小值 \(0\)
考虑 \(k == 2\) 的部分分,是在看两点之间是否存在长度为偶数的路径,那么可以进行染色
我们考虑更一般的情况
首先一个连通块以及模数 \(k\), 能够表示出的数都是连通块内所有边边权和 \(k\) 的 \(gcd\)
我们把他们都除掉 \(gcd\) 最后再乘上一定是对的,记 \(k'\) 为除掉 \(gcd\) 之后的 \(k\)
那么 \(k'\) 为奇数,跟最开始说的没有区别,答案为 \(0\)
考虑 \(k'\) 为偶数,根据裴蜀定理,一定能表示出 \(gcd\) 即 \(1\)
我们考虑从 \(u\) 出发回到 \(u\), 每次如果能变化 \(1\), 那么答案为 \(0\)
但是不一定能够回来,考虑把每条边经过次数 \(\times 2\) 那么度数都为偶数一定存在欧拉回路
所以一般情况下答案最大为 \(1\)
什么时候取 \(1\), 什么时候取 \(0\)
因为每次可以让答案变化 \(2\) 所以跟 \(k == 2\) 的部分一样染色,看是否存在长度为偶数的路径即可
边权的奇偶性与因子中 \(2\) 的个数有关,如果 \(k‘\) 是偶数,那么边权 \(gcd\) 的 \(2\) 已经全部去掉了,所以询问不会改变边权的奇偶性
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 2e5 + 55;
int n, m, q;
struct edge{int u, v, w;}e[maxn];
struct DSU{
int f[maxn], g[maxn];
void init(){for(int i = 1; i <= n; ++i)f[i] = i;}
int fa(int x){return f[x] == x ? x : f[x] = fa(f[x]);}
void link(int u, int v, int w){
u = fa(u); v = fa(v);
g[u] = __gcd(g[u], __gcd(g[v], w));
f[v] = u;
}
int query(int x, int y){return fa(x) == fa(y) ? g[fa(x)] : 0;}
}s;
struct EXDSU{
int f[maxn];
void init(){for(int i = 1; i <= n + n; ++i)f[i] = i;}
int fa(int x){return f[x] == x ? x : f[x] = fa(f[x]);}
void merge(int x, int y){f[fa(y)] = fa(x);}
int query(int x, int y){return fa(x) == fa(y);}
}c;
int main(){
n = read(), m = read(), q = read();
s.init(); c.init();
for(int i = 1; i <= m; ++i){
int u = read(), v = read(), w = read();
e[i] = {u, v, w}; s.link(u, v, w);
}
for(int i = 1; i <= m; ++i){
e[i].w /= s.query(e[i].u, e[i].v);
if(e[i].w & 1) c.merge(e[i].u, e[i].v + n), c.merge(e[i].u + n, e[i].v);
else c.merge(e[i].u, e[i].v), c.merge(e[i].u + n, e[i].v + n);
}
for(int i = 1; i <= q; ++i){
int u = read(), v = read(), k = read(), g;
if(g = s.query(u, v)){
if(((k / __gcd(k, g)) & 1) || c.query(u, v))printf("0\n");
else printf("%d\n", __gcd(k, g));
}else printf("NIE\n");
}
return 0;
}
B. Hack
直接跑最小割会让一条路径上存在不止一条选中的边,考虑如何避免这种情况
发现如果一条路径被选择了多个位置,那么一定是存在类似横叉边的东西
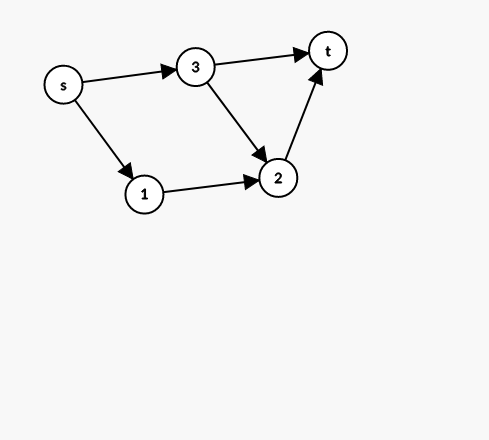
如割断 \(s -> 3\) 和 \(2 - > t\)
我们需要强制要求不能同时割断\(s -> 3\) 和 \(2 - > t\)
换句话说就是 \(s - > 2\) 和 \(3 - > t\) 必然割掉至少一段
那么建立反向流量为 \(inf\) 的边即可
注意删去 \(s\) 到不了的点,不然
你看这个跑出来是啥
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const ll inf = 1e15;
const int maxn = 205;
const int maxm = 10005;
int n, m;
struct WWL{
int s, t;
int head[maxn], tot = 1;
struct edge{int to, net; ll val;}e[maxm];
void add(int u, int v, ll w){
e[++tot].net = head[u];
head[u] = tot;
e[tot].to = v;
e[tot].val = w;
}
void link(int u, int v, int w){add(u, v, w); add(v, u, inf);}
int dep[maxn], now[maxn];
bool bfs(){
memset(dep, 0, sizeof(dep));
queue<int>q; dep[s] = 1; q.push(s);
now[s] = head[s];
while(!q.empty()){
int x = q.front(); q.pop();
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(!flag[v])continue;
if(e[i].val > 0 && dep[v] == 0){
dep[v] = dep[x] + 1;
now[v] = head[v];
if(v == t)return true;
q.push(v);
}
}
}
return false;
}
ll dfs(int x, ll from){
if(x == t || from <= 0)return from;
ll res = from; int i;
for(i = now[x]; i; i = e[i].net){
int v = e[i].to;
if(e[i].val > 0 && dep[v] == dep[x] + 1){
ll k = dfs(v, min(res, e[i].val));
if(k <= 0)dep[v] = 0;
e[i].val -= k;
e[i ^ 1].val += k;
res -= k;
if(res <= 0)break;
}
}
now[x] = i;
return from - res;
}
ll dinic(){
ll ans = 0;
while(bfs())ans += dfs(s, inf);
return ans;
}
bool flag[maxn];
void dfs(int x){
flag[x] = 1;
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(e[i].val > 0 && e[i].val < 1e9)if(!flag[v])dfs(v);
}
}
void init(){
int n = read(), m = read();
s = 1, t = n;
for(int i = 1; i <= m; ++i){
int u = read() + 1, v = read() + 1, w = read();
link(u, v, w);
}
dfs(1);
ll ans = dinic();
printf("%lld\n",ans > 1e12 ? -1 : ans);
}
}w;
int main(){
w.init();
return 0;
}
C. Sanrd
一个 \(lis\) 与一个 \(lds\) 的交集至多一个点
先计算出每个数,在多少 \(lds\) 中
再去跑 \(lis\)
如果 \(lis\) 选中的点的 \(lds\) 方案数之和不等于总数
那么一定存在合法方案
具体的,如果一个数存在两个前驱,他们的方案数不同,那么如果这个数能构成 \(lis\),两个前驱必然有一个合法,也就能够构造出解
于是在 \(lis\) 时对每个点维护两个前驱
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> pii;
int read(){
int x = 0; char c = getchar();
while(!isdigit(c))c = getchar();
do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
return x;
}
const int maxn = 5e5 + 55, mod = 1e9 + 7;
int n, a[maxn];
#define lowbit(x) (x & -x)
int Mod(int x){return x >= mod ? x - mod : x;}
struct maxs{
int len, sum;
maxs(){len = sum = 0;}
maxs(int a, int b){len = a; sum = b;}
friend maxs operator + (const maxs &x, const maxs &y){
return x.len > y.len ? x : (x.len < y.len ? y : maxs(x.len, Mod(x.sum + y.sum)));
}
void clear(){len = sum = 0;}
};
struct BIT_MAX_SUM{
maxs t[maxn];
void insert(int x, maxs val){while(x <= n){t[x] = t[x] + val; x += lowbit(x);}}
maxs query(int x){maxs ans; while(x){ans = ans + t[x]; x -= lowbit(x);} return ans;}
void clear(){for(int i = 1; i <= n; ++i)t[i].clear();}
}tms;
struct data{
int len, prea, preb, plana, planb;
data(){len = prea = preb = plana = planb = 0;}
data(int a, int b, int c, int d, int e){len = a; prea = b; preb = c; plana = d; planb = e;}
friend data operator + (const data &x, const data &y){
if(x.len != y.len)return x.len > y.len ? x : y;
if(x.plana != x.planb)return x;
if(y.plana != y.planb)return y;
return data(x.len, x.prea, y.prea, x.plana, y.plana);
}
};
struct BIT_DATA{
data t[maxn];
void insert(int x, data val){while(x <= n){t[x] = t[x] + val; x += lowbit(x);}}
data query(int x){data ans; while(x){ans = ans + t[x]; x -= lowbit(x);} return ans;}
}td;
struct mxlen{
int len, pos;
mxlen(){len = pos = 0;}
mxlen(int a, int b){len = a; pos = b;}
friend mxlen operator + (const mxlen &x, const mxlen &y){
return x.len > y.len ? x : y;
}
};
struct BIT_MAX_LEN{
mxlen t[maxn];
void insert(int x, mxlen val){while(x <= n){t[x] = t[x] + val; x += lowbit(x);}}
mxlen query(int x){mxlen ans; while(x){ans = ans + t[x]; x -= lowbit(x);} return ans;}
}tml;
int lds, lis, ldsf, fd[maxn], ld[maxn], pre[maxn];
bool vis[maxn];
data rem[maxn];
vector<int>lispos;
void dfs(int pos, int plan){
if(pos == 0)return;
if(rem[pos].plana == plan)dfs(rem[pos].prea, Mod(plan + mod - fd[pos]));
else dfs(rem[pos].preb, Mod(plan + mod - fd[pos]));
lispos.push_back(pos);
}
void print(int pos){
if(pos == 0)return;
if(pre[pos])print(pre[pos]);
printf("%d ",pos);
}
int main(){
freopen("sanrd.in","r",stdin);
freopen("sanrd.out","w",stdout);
n = read();
for(int i = 1; i <= n; ++i)a[i] = read();
for(int i = 1; i <= n; ++i){
maxs tmp = tms.query(n - a[i] + 1);
if(tmp.len == 0)tmp.sum = 1;
++tmp.len; fd[i] = tmp.sum; ld[i] = tmp.len;
tms.insert(n - a[i] + 1, tmp);
}
tms.clear();
for(int i = n; i >= 1; --i){
maxs tmp = tms.query(a[i]);
if(tmp.len == 0)tmp.sum = 1;
ld[i] += tmp.len; fd[i] = 1ll * fd[i] * tmp.sum % mod;
++tmp.len;
tms.insert(a[i], tmp);
}
for(int i = 1; i <= n; ++i)lds = max(ld[i], lds);
for(int i = 1; i <= n; ++i)if(ld[i] != lds)fd[i] = 0;
ldsf = tms.query(n).sum;
for(int i = 1; i <= n; ++i){
data tmp = td.query(a[i]);
++tmp.len;
tmp.plana = Mod(tmp.plana + fd[i]);
tmp.planb = Mod(tmp.planb + fd[i]);
rem[i] = tmp;
tmp.prea = tmp.preb = i;
td.insert(a[i], tmp);
}
data lised = td.query(n); lis = lised.len;
if(lised.plana == lised.planb && lised.plana == ldsf){
printf("-1\n"); return 0;
}
printf("%d\n",lis);
if(lised.plana == ldsf)dfs(lised.preb, lised.planb);
else dfs(lised.preb, lised.plana);
for(int v : lispos)printf("%d ",v); printf("\n");
for(int v : lispos)vis[v] = true;
printf("%d\n",lds);
for(int i = 1; i <= n; ++i)if(!vis[i]){
mxlen tmp = tml.query(n - a[i] + 1);
pre[i] = tmp.pos;
++tmp.len; tmp.pos = i;
tml.insert(n - a[i] + 1, tmp);
}
print(tml.query(n).pos);
printf("\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号