卡特兰数 pufer序列 bsgs

卡特兰数

卡特兰数

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440......

设\(h(n)\)为\(catalan\)数的第\(n\)项

\(h(0)=1\),\(h(1)=1\)

\(h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n≥2)\)

\(h(n)=h(n-1)*(4*n-2)/(n+1)\)

\(h(n)=C(2n,n)/(n+1)\).................(1)

\(h(n)=C(2n,n) - C(2n,n-1)\)..................(2)

用图比较好理解

卡特兰数有一个很重要的意义就是：
\(C_n\)表示所有在\(n×n\)格点中不越过对角线的单调路径的个数（只向上向右走）

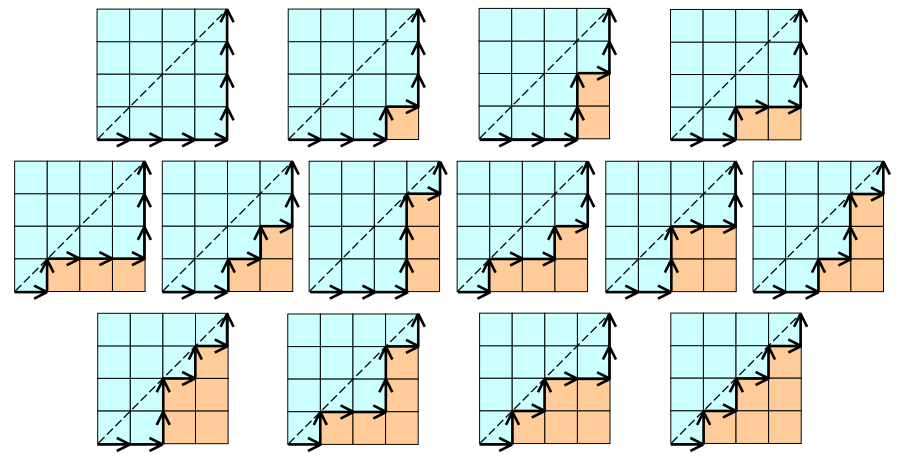
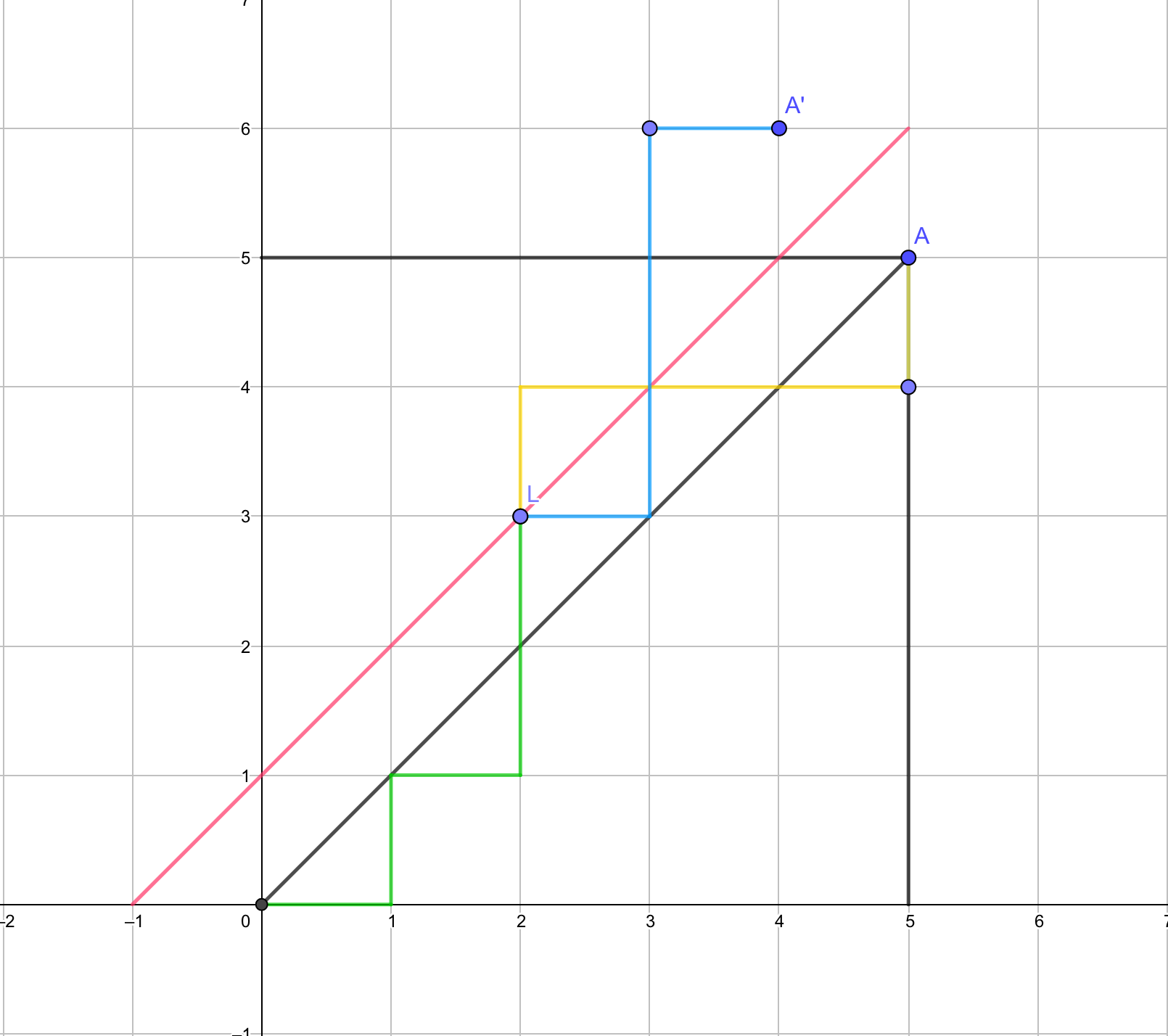
不考虑不越过对角线这个条件，有\(C_{2n}^n\)种方案，对每个越过对角线的不合法方案，一定经过\(y=x+1\)这条直线，从路径与该直线的第一个交点处开始，剩余路径进行镜像处理（关于直线对称），终点一定是\((n,n)\)关于直线的对称点\((n-1,n+1)\)每一条\((0,0)->(n-1,n+1)\)的路径，对应一条计数的非法路径，所以合法路径数为

\(C_{2n}^n-c_{2n}^{n-1}\)

得到公式\((2)\)，展开通分整理得到\((1)\)

例题

网格

用类似卡特兰数证明得到答案为

\(C_{n+m}^n-C_{n+m}^{n+1}\)

展开整理

\((n+m)!*(n-m+1)/(n+1)!m!\)

分解质因数约分，然后高精乘统计答案

有趣的数列

可以看成将长度为\(2n\)的排列分成两个排列，那么一共有\(C_{2n}^n\)种

考虑条件3，偶数位里面一个偶数要比前面的偶数位大，而这些数位又比和他们对应的奇数位大，所以我们可以得到：

对于任意偶数位，这里放的数都大于前面的所有数

换句话说，就算前面所有位置都放尽可能小的数，这个位置最小也就只能放跟它下标一样大的数了（位置4只能放大于等于4的值）

我们转换一下题意，变成1~2n一次放入这个数列里，对于每次放的数要么放在最前的奇数位，要么放在最前的偶数位。

联系前面的结论，我们可以知道：一个数列如果有偶数个数多于奇数个数的情况，就不可能满足条件了

放一个偶数看作坐标系中向上走一步，放一个奇数看作向右，可以得到卡特兰数

树屋阶梯

大佬的题解

每次放的钢块一定有一个阶梯角，考虑阶梯角在哪里的钢块覆盖了\((n,0)\)，然后余下部分记录方案，可以得到卡特兰数，具体过程图解大佬的博客讲的很清楚，蒟蒻就不多说了

pufer序列

pufer序列与无根树存在对应关系

\(n\)个点的无根树得到的pufer序列长度为\(n-2\)

如果令编号小的点优先，那么pufer序列与无根树唯一对应

由无根树得到pufer序列

• 找到编号最小的叶节点，将他的父亲加入pufer序列，删除该节点

• 重复操作至剩余两个节点

pufer序列转无根树

• 取出prufer序列最前面的元素x

• 取出在点集中的、且当前不在prufer序列中的最小元素y

• 在x,y之间连接一条边

• 最后在点集中剩下的两个点中连一条边

性质：

1. pufer序列与无根树一一对应

2. 度数为k的点在pufer序列中出现k-1次

3. 一个n个点的完全图的生成树的个数为\(n^{n-2}\)

对于一个n个点的无根树，它的prufer序列长为n−2，而每个位置有n种可能性，因此可能的prufer序列有\(n^{n-2}\)种,prufer序列与无根树一一对应，因此生成树个数\(n^{n-2}\)

4. 对于给定度数为\(d_{1\sim n}\)的一棵无根树共有\(\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}\)种情况。

\((1)\)由上面的性质可以知道，度数为\(d_i\)的节点会在\(prufer\)序列中出现\(d_{i-1}\)次

则就是要求出\(d_{i-1}\)个\(i(1\le i\le n)\)的全排列个数。

而上面那个式子就是可重全排列公式。（即全排列个数除以重复元素内部的全排列个数）

(2)另一种理解方式

有\(n-2\)个位置，要放\(n\)个数，数\(i\)要占\(d[i]-1\)个位置

这就变成了一个简单的组合数问题，\(ans = \prod_{i=1}^nC_{d[i] - 1} ^ {sum}\)其中sum为剩余的位置数

树的计数

套用公式，注意

1. 边乘边除/高精/组合数/python
2. 判无解

明明的疑惑

我真是太疑惑了，高精乘进位写成\(+=\)调了半天没想到高精出锅了。。

设

\(sum=\sum_{i=1}^nd[i]-1(d[i]!=-1)\)

\(cnt=\sum_{i=1}^n(d[i]!=-1)\)

如果\(d[i]==0\)或者\(sum>n-2\)显然不合法，直接判无解

因为\(pufer\)序列与无根树一一对应，考虑能生成多少序列

有度的点在序列中占用了\(sum\)个位置，有\(C_{n-2}^{sum}\)种选法

又有每个点的度数要求，就是知道了每个点在序列中的出现次数，那么对这些点可能的排列有\(\frac {sum!} { \Pi_{i=1}^n(d[i]-1)!}(d[i]!=-1)\)

序列剩下\(n-2-sum\)个位置，每个位置都是\(n-cnt\)种选择有\((n-cnt)^{n-2-sum}\)种

最后的式子是
\(C_{n-2}^{sum}\frac {sum!} { \Pi_{i=1}^n(d[i]-1)!}(n-cnt)^{n-2-sum}(d[i]!=-1)\)

展开化简得\(\frac {(n-2)!} { \Pi_{i=1}^n(d[i]-1)!(n-2-sum)!}(n-cnt)^{n-2-sum}(d[i]!=-1)\)

BSGS(基础)

大步小步算法，常用于解决离散对数问题

即求解\(a^x\equiv b(mod\;p)(a\perp p)\)其中方程的解满足\(0 \leq x < p\)

设\(x=A \lceil \sqrt p \rceil \ -B\)

其中$A,B \in [0,\lceil \sqrt p \rceil] $

有

\(a^{A \lceil \sqrt p \rceil -B}\equiv b(mod\;p)\)

变形

\(a^{A \lceil \sqrt p \rceil }\equiv b*a^B(mod\;p)\)

枚举\(B\)计算\(b*a^B\),用\(map/hash\)存一下

再枚举\(A\)计算\(a^{A \lceil \sqrt p \rceil }\)在\(hash/map\)查找对应值

解为\(x=A \lceil \sqrt p \rceil \ -B\)

如果没有找到则无解

时间复杂度枚举\(A,B\)均为\(\sqrt p\)所以总复杂度\(O(\sqrt p)\)使用\(map\)会多一个\(log\)

随机数生成器

推式子

\(x_2=(ax_1+b)\%p\)

\(x_3=(ax_2+b)\%p=(a^2x_1+ab+b)\%p\)

\(x_4=(ax_3+b)\%p=(a^3x_1+a^2b+ab+b)\%p\)

\(x_i=(ax_{i-1}+b)\%p=(a^{i-1}x_1+b\sum_{j=0}^{i-2}a^j)\%p\)

设

\(S=\sum_{j=0}^{i-2}a^j\)

\(aS=\sum_{j=1}^{i-1}a^j\)

\((a-1)S=a^{i-1}-1\)

\(S=(a^{i-1}-1)/(a-1)\)

\(x_i=(a^{i-1}x_1+b(a^{i-1}-1)/(a-1))\%p\)

问题转化为

判断

\(t\equiv (a^{i-1}x_1+b(a^{i-1}-1)/(a-1))(mod\;p)\)

是否有解

移项整理，求一下逆元，然后就是裸的\(bsgs\)

注意在\(a=1\)时是个不定方程，扩欧解决，\(a=0\)直接特判

计算器

裸题

Discrete Logging

裸题

Matrix

同样的方法，写个矩阵哈希就行了，可以写两个防止挂掉