[数据结构与算法-14]存图

存图

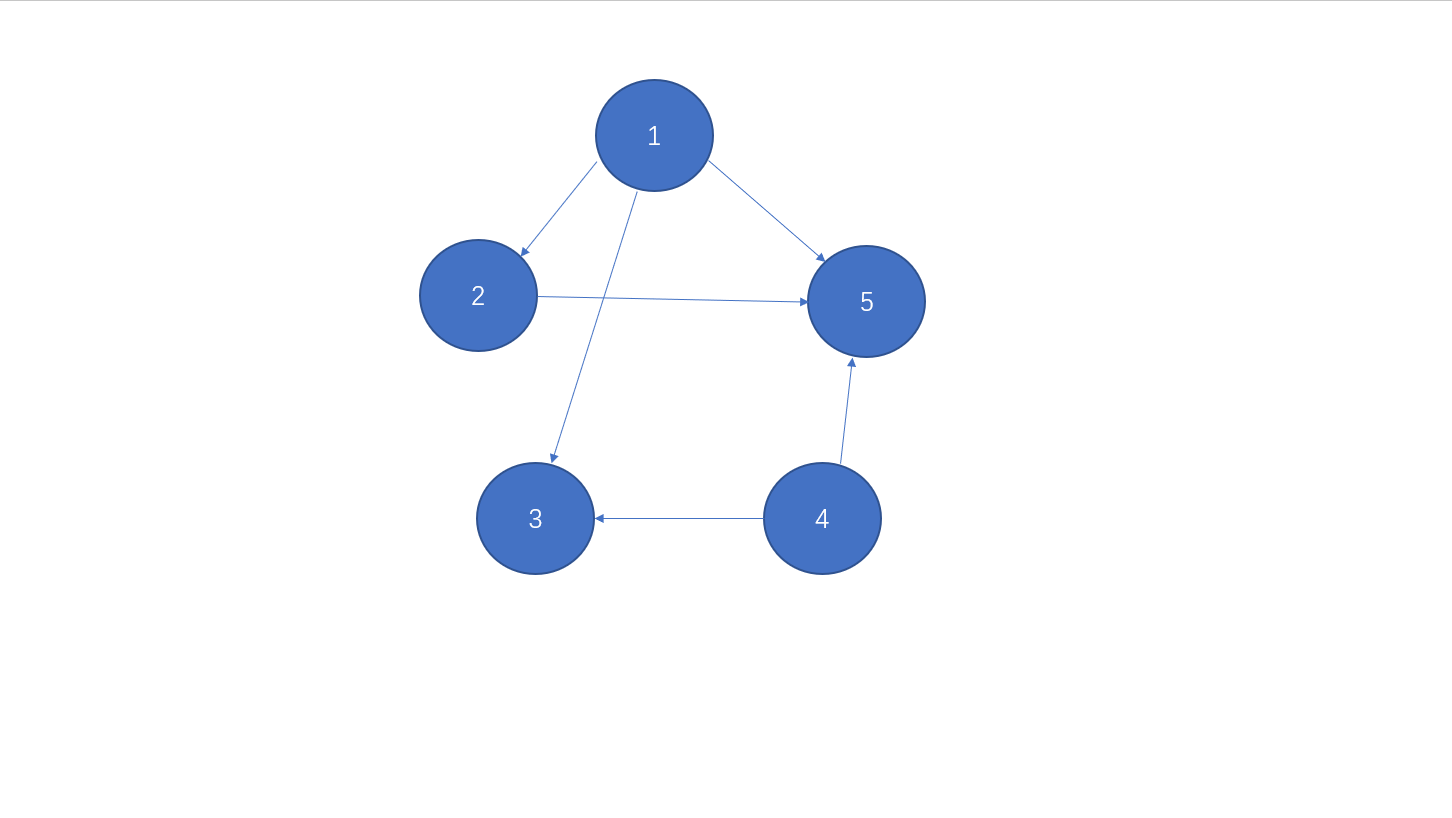
假设输入数据为\(u\),\(v\),\(w\),分别为开始点， 结束点，边权

邻接矩阵

用一个矩阵来保存两点之间的联系

\[\left(\begin{matrix} 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ \end{matrix}\right) \]

r -> c	1	2	3	4	5
1	0	1	1	0	1
2	0	0	0	0	1
3	0	0	0	0	0
4	0	0	1	0	1
5	0	0	0	0	0

cin >> u >> v >> w;
A[u][v] = w;

邻接表

用一个数组\(A[i]\)保存从\(i\)发出的所有边

构造边

struct edge{
    int to, w;
}

利用vector

#include <vector>
std::vector<edge> edges[MAX];
// 有向图
void add(int from, int to, int w){
    edges[from].push_back(edge({to, w}));
}
// 无向图
add(from, to, w);
add(to, from, w);

链式向前星

用数组模拟图

构造边

// next用来指向下一条边
struct edge{
    int to, w, next;
}

构造头

// head[i]保存从i发出的第一条边
int head[MAX];

构造数组存储所有的边

edge edges[MAX];

添加

// 用cnt保存当前边的条数
void add(from, to, w){
    edges[++cnt].w = w;
    edges[cnt].to = to;
    // 将下一条边指向当前的第一条边
    edges[cnt].next = head[from];
    // 更新第一条边为当前边
    head[from] = cnt;
}

遍历

for (int i = head[from];i;i = edges[i].next)
    printf("%d", edges[i].to);

head	var
0	0
1	1
2	4
3	0
4	5
5	0

edges	var
0	0
1	to=2,next=2
2	to=3,next=3
3	to=5,next=0
4	to=5,next=0
5	to=3,next=6
6	to=5,next=0