[数据结构与算法-11]三分法

三分法

作用

求函数的驻点

思路

从高数或者大雾借鉴的思路，只要数值求导即可，加上二分法的思想

题目描述

如题，给出一个 N 次函数，保证在范围 [l, r]内存在一点 xx，使得 [l, x] 上单调增，[x, r] 上单调减。试求出 x 的值。

输入格式

第一行一次包含一个正整数 NN 和两个实数 l, r 含义如题目描述所示。

第二行包含 N + 1个实数，从高到低依次表示该 NN 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 x 的值。若你的答案与标准答案的相对或绝对误差不超过 \(10^{-5}\)则算正确。

输入输出样例

输入 #1复制

3 -0.9981 0.5
1 -3 -3 1

输出 #1复制

-0.41421

说明/提示

对于 \(100\%\) 的数据，\(6 \le N \le 13\)，函数系数均在 [-100,100] 内且至多 15 位小数，\(|l|,|r|\leq 10\) 且至多 15 位小数。\(l\leq r\)。

【样例解释】

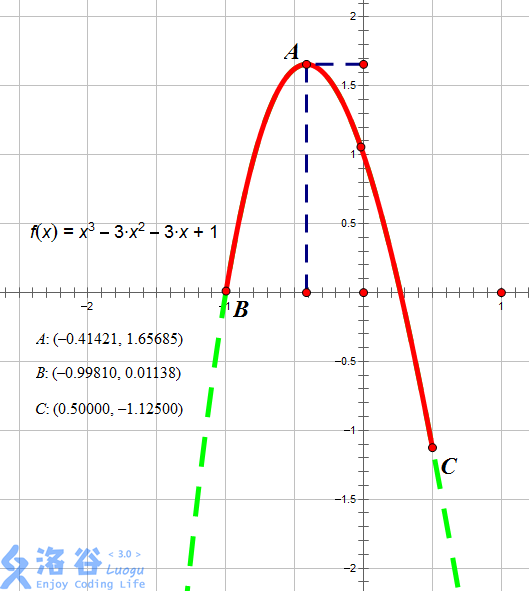
如图所示，红色段即为该函数 \(f(x) = x^3 - 3 x^2 - 3x + 1\) 在区间 [-0.9981, 0.5] 上的图像。

当 x = -0.41421 时图像位于最高点，故此时函数在 [l, x] 上单调增，[x, r] 上单调减，故 x = -0.41421，输出 -0.41421。

完整解答

#include <cstdio>
#include <cmath>
float error = 1E-7;
int N;
double l, r, a[15], mid1, mid2;
double f(double x) {
	double ans = 0, p = N;
	for (int i = 1; i <= N+1; i++)
		ans += a[i]*pow(x, p--);
	return ans;
}
int main() {
	scanf("%d%lf%lf", &N, &l, &r);
	for (int i = 1; i <= N+1; i++)
		scanf("%lf", a+i);
	while (fabs(l - r) >= error)
	{
		double mid = (l + r) / 2;
		if (f(mid + error) > f(mid - error)) l = mid;
		else r = mid;
	}
	printf("%lf\n", (l + r) / 2);
	return 0;
}