[数据结构与算法-04]树状数组
树状数组
数组的存储方式
-
数组建议从索引1开始
-
单点存储 (存储单个数的值)
- 单点查询与修改快
- 查询:
a[i] - 修改:
a[i] += delta
- 查询:
- 区间查询与修改慢
- 查询:\(\Sigma a[i]\)
- 修改:
for (int index = i; index <= j; index++) a[index] += delta;
- 单点查询与修改快
-
前缀和 (存储前n项和)
-
单点查询快,单点修改慢
- 查询:
s[i] - s[i-1] - 修改:
for (int index = i; index <= len; index++) s[index] += delta;
- 查询:
-
区间查询快,区间修改慢
- 查询:
s[j] - s[i-1] - 修改:太麻烦就不写了,每修改一个点,从此以后的所有点都要改变
- 查询:
-
-
差分 (存储当前元素与前一元素值之差
d[i] = a[i] - a[i-1])- 单点查询慢,单点修改快
- 查询:\(\Sigma d[i]\)
- 修改:
d[i] += delta;d[i+1] -= delta;
- 区间查询慢,区间修改快
- 查询:\(\Sigma\Sigma d[i]\)
- 修改:
d[i] += delta;d[j+1] -= delta;
- 单点查询慢,单点修改快
树状数组
树状数组可看为单点存储和前缀和的折中,树状数组的索引用二进制表示,可实现较快的区间查询与单点修改
树状数组数据的组织方式
我们定义,二进制数x最右边的一个1,连带着它之后的0为 lowbit(x)。比如(10100)2的lowbit就是(00100)2,每个点表示区间(Ai-lowbit(Ai), Ai]的数值之和
lowbit
#define lowbit(x) ((x)&(-x))
查询
- 仿照前缀和,要求出前n项和:
- 当前区间的值:ans += tree[Ai]
- 在此区间之前的所有值:ans += query(Ai-lowbit(Ai))
- 循环版本:
for (int index = n; index; index -= lowbit(index)) ans += tree[index];
- 单点查询:query(i) - query(i - 1)
- 区间查询:query(j) - query(i - 1)
修改
- 所有包含要修改元素的区间都要修改,查询相当于向下爬树,修改要向上爬树,反过来即可 :
for (int index = i; index <= len; index += lowbit(index)) tree[index] += delta;
P3374 【模板】树状数组 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某一个数加上 x
- 求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,m 分别表示该数列数字的个数和操作的总个数。
第二行包含 n 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 m 行每行包含 33 个整数,表示一个操作,具体如下:
1 x k含义:将第 x 个数加上 k2 x y含义:输出区间 [x,y] 内每个数的和输出格式
输出包含若干行整数,即为所有操作 22 的结果。
输入输出样例
输入 #1复制
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4输出 #1复制
14 16说明/提示
【数据范围】
对于 30% 的数据,1 \le n \le 81≤n≤8,1\le m \le 101≤m≤10;
对于 70% 的数据,1\le n,m \le 10^41≤n,m≤104;
对于 100% 的数据,1\le n,m \le 5\times 10^51≤n,m≤5×105。
完整解答
#include <cstdio>
#define MAX 500000
#define lowbit(x) ((x)&(-x))
short flag;
int temp, n, m, x, y, k, cnt = 0;
int num[MAX + 1]{ 0 };
void update(int index, int var) {
for (int pos = index; pos < MAX + 1; pos += lowbit(pos))
num[pos] += var;
}
int query(int n) {
if (n <= 0)return 0;
int ans = 0;
for (int pos = n; pos; pos -= lowbit(pos)) ans += num[pos];
return ans;
}
int query(int s, int e) {
return query(e) - query(s);
}
int main() {
scanf("%d%d", &n, &m);
for (int index = 1; index < n+1; index++) {
scanf("%d", &temp);
update(index, temp);
}
for (int index = 0; index < m; index++) {
scanf("%hd", &flag);
if (flag == 1) {
scanf("%d%d", &x, &k);
update(x, k);
}else if (flag == 2) {
scanf("%d%d", &x, &y);
printf("%d\n", query(x-1, y));
}
}
return 0;
}
题目描述
如题,已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数数加上 xx;
- 求出某一个数的值。
输入格式
第一行包含两个整数 NN、MM,分别表示该数列数字的个数和操作的总个数。
第二行包含 NN 个用空格分隔的整数,其中第 ii 个数字表示数列第 ii 项的初始值。
接下来 MM 行每行包含 22 或 44个整数,表示一个操作,具体如下:
操作 11: 格式:
1 x y k含义:将区间 [x,y][x,y] 内每个数加上 kk;操作 22: 格式:
2 x含义:输出第 xx 个数的值。输出格式
输出包含若干行整数,即为所有操作 22 的结果。
输入输出样例
输入 #1复制
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4输出 #1复制
6 10说明/提示
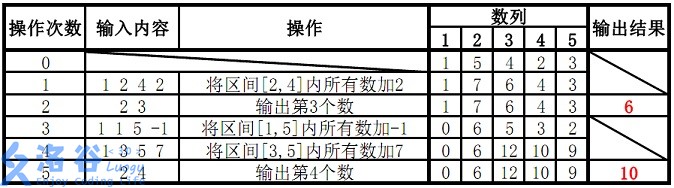
样例 1 解释:
故输出结果为 6、10。
数据规模与约定
对于 30%30% 的数据:N\le8,M\le10N≤8,M≤10;
对于 70%70% 的数据:N\le 10000,M\le10000N≤10000,M≤10000;
对于 100%100% 的数据:1 \leq N, M\le 5000001≤N,M≤500000,1 \leq x, y \leq n1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 2^{30}230。
完整解答
// 将差分数组和树状数组结合即可
#include <cstdio>
#define MAX 500000
#define lowbit(x) ((x)&(-x))
short flag;
int n, m, x, y, k, cnt = 0;
int num[MAX + 10]{ 0 };
void update(int index, int var) {
for (int pos = index; pos < MAX + 1; pos += lowbit(pos))
num[pos] += var;
}
int query(int n) {
if (n <= 0)
return 0;
int ans = 0;
for (int pos = n; pos; pos -= lowbit(pos))
ans += num[pos];
return ans;
}
int main() {
scanf("%d%d", &n, &m);
int l = 0,r;
for (int index = 1; index < n + 1; index++) {
scanf("%d", &r);
update(index, r - l);
l = r;
}
for (int index = 0; index < m; index++) {
scanf("%hd", &flag);
if (flag == 1) {
scanf("%d%d%d", &x, &y, &k);
update(x, k);
update(y + 1, -k);
}
else if (flag == 2) {
scanf("%d", &x);
printf("%d\n", query(x));
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号