深度图与点云去噪实战:双边滤波+统计/半径滤波原理与Open3D全实现
前言
在3D计算机视觉领域,深度相机(RealSense、Kinect、LiDAR)采集的深度图/点云数据不可避免会引入噪声——比如椒盐噪声、孤立点、稀疏噪点簇、高斯噪声等。这些噪声会直接影响后续的3D重建、点云配准、目标分割等任务的精度,因此针对性去噪是3D数据预处理的核心步骤。
本文将从实际应用出发,先详细讲解点云去噪中经典的统计滤波和半径滤波(结合你提供的Open3D工业级代码逐行解析),再深入剖析深度图去噪的核心算法双边滤波(原理+实现+调优),最后实现深度图双边滤波+点云统计/半径滤波的全流程去噪方案,兼顾边缘保留和平滑去噪,适配大部分工业级场景。
@
前置知识与环境准备
核心依赖
本文所有代码基于Python实现,需安装以下库:
pip install open3d numpy opencv-python matplotlib
open3d:3D点云处理核心库,提供滤波、可视化、格式转换等功能;numpy:数值计算基础,处理深度图/点云的数组数据;opencv-python:2D深度图的双边滤波、图像读写;matplotlib:深度图滤波效果可视化。
噪声类型说明
深度图/点云的常见噪声及对应解决方案:
- 孤立点/椒盐噪声:单个离散的噪点,无邻域点,用统计滤波剔除;
- 稀疏噪点簇:几个噪点聚集在一起,统计滤波无法识别,用半径滤波剔除;
- 高斯噪声/均匀噪声:深度图上的平滑噪声,会模糊但不破坏边缘,用双边滤波平滑,且保留物体轮廓;
- 密集小噪点团:少量噪点紧密聚集,可选3D形态学开运算处理(牺牲少量细节)。
第一部分:点云去噪基础——统计滤波&半径滤波
核心是统计滤波+半径滤波的组合,还做了超大点数优化、低版本Open3D兼容、无效点剔除等实用设计。这部分先讲两个滤波的核心原理,再逐行解析代码,让你知其然更知其所以然。
1.1 统计滤波(Statistical Outlier Removal)
核心原理
统计滤波的核心思想是基于邻域点的距离统计特性剔除异常点,假设点云的正常点在空间中是连续分布的,噪点与邻域点的距离会远大于正常点。
具体步骤:
- 对每个点,计算其到k个最近邻点的欧式距离的平均值;
- 所有点的平均距离服从高斯分布,计算该分布的均值$\mu$和标准差$\sigma$;
- 剔除平均距离超过$\mu + std_ratio \times \sigma$的点(即距离远于正常范围的孤立点)。
核心用途
专门剔除单点椒盐噪声、离散孤立点,是点云去噪的第一步基础操作,几乎所有点云去噪流程都会先做统计滤波。
关键参数
nb_neighbors:每个点的近邻数,一般取20~50(点数越多取越大);std_ratio:标准差系数,一般取1.0~2.0(噪声越严重,系数越小,剔除越严格)。
1.2 半径滤波(Radius Outlier Removal)
核心原理
半径滤波是统计滤波的补充,解决统计滤波对“小噪点簇”无效的问题,核心是基于邻域点的数量剔除异常点。
具体步骤:
- 以每个点为球心,设置一个固定半径r,构建3D球形邻域;
- 统计球形邻域内的点数量,剔除数量少于
min_nn的点; - 即使几个噪点聚集,其邻域内的点数仍会远少于正常点,因此能被有效剔除。
核心用途
专门剔除稀疏小噪点簇(2~5个噪点聚集),与统计滤波组合形成“孤立点+小簇噪点”的全覆盖剔除,是点云去噪的黄金组合。
关键参数
radius:球形邻域半径(单位:米),一般取0.03~0.1m(根据点云密度调整,密度越大半径越小);min_nn:邻域内最小有效点数,一般取8~15(与radius匹配,半径越大,最小点数取越大)。
1.3 工业级点云去噪代码逐行解析(你的PLY代码)
你提供的代码做了很多工业级优化(低版本兼容、超大点数防内存溢出、可选形态学开运算),以下分模块解析核心逻辑,标注关键亮点和参数调优技巧。
完整代码(带详细注释+优化说明)
import open3d as o3d
import numpy as np
def ply_denoise(
input_ply_path, # 输入带噪PLY文件路径
output_ply_path, # 输出去噪后PLY文件路径
# 统计滤波参数:去3D孤立点
stat_nb_neighbors=20,
stat_std_ratio=2.0,
# 半径滤波参数:去稀疏小噪点簇(单位:米)
rad_radius=0.05,
rad_min_nn=10,
# 可选3D形态学开运算(类似2D腐蚀,处理密集小噪点团)
use_morphology=False,
morph_voxel_size=0.02,
# 超大点数点云专属:轻量体素下采样(默认开启,降低计算量)
use_down_sample=True,
down_voxel_size=0.01
):
"""
PLY点云文件去噪:低版本Open3D兼容+超大点数点云优化
核心:统计滤波+半径滤波,支持带颜色/无颜色PLY,保留点云原始信息
调优原则:噪声越严重,stat_std_ratio越小、rad_radius越大、rad_min_nn越大
"""
# 1. 读取PLY点云文件,校验有效性
print(f"正在读取PLY文件:{input_ply_path}")
pcd = o3d.io.read_point_cloud(input_ply_path)
if not pcd.has_points():
raise ValueError("读取PLY失败!文件损坏或非点云文件")
original_point_num = len(pcd.points)
print(f"原始点云点数:{original_point_num:,}") # 千分位显示,提升可读性
# 2. 核心预处理:无效点+重复点剔除【低版本Open3D兼容亮点】
# remove_infinite=True 适配所有Open3D版本(旧版本无remove_inf)
pcd = pcd.remove_non_finite_points(remove_nan=True, remove_infinite=True)
pcd = pcd.remove_duplicated_points() # 剔除重复点,避免邻域统计误差
preprocess_point_num = len(pcd.points)
if original_point_num - preprocess_point_num > 0:
print(f"预处理:剔除{original_point_num - preprocess_point_num:,}个无效/重复点")
# 3. 超大点数优化:体素下采样【工业级亮点,防内存溢出】
# 点数超100万开启,通过体素化降低点数,不影响整体结构
if use_down_sample and preprocess_point_num > 1000000:
pcd = pcd.voxel_down_sample(voxel_size=down_voxel_size)
down_point_num = len(pcd.points)
print(f"超大点数优化:体素下采样后点数{down_point_num:,}(体素大小{down_voxel_size}m)")
else:
down_point_num = preprocess_point_num
# 4. 核心去噪:统计滤波+半径滤波【黄金组合,全覆盖离散噪点】
# 4.1 统计滤波:去孤立点
cl, ind = pcd.remove_statistical_outlier(nb_neighbors=stat_nb_neighbors, std_ratio=stat_std_ratio)
pcd_denoised = pcd.select_by_index(ind)
stat_remove = down_point_num - len(pcd_denoised.points)
print(f"统计滤波:剔除{stat_remove:,}个孤立噪点")
# 4.2 半径滤波:去稀疏小噪点簇(统计滤波的补充)
cl, ind = pcd_denoised.remove_radius_outlier(nb_points=rad_min_nn, radius=rad_radius)
pcd_denoised = pcd_denoised.select_by_index(ind)
rad_remove = down_point_num - stat_remove - len(pcd_denoised.points)
print(f"半径滤波:剔除{rad_remove:,}个稀疏噪点")
# 5. 可选:3D形态学开运算【处理密集小噪点团,牺牲少量细节】
# 原理:先腐蚀(剔除小簇噪点)后膨胀(恢复正常点云结构)
if use_morphology:
print(f"开启3D开运算(腐蚀+膨胀),体素大小{morph_voxel_size}m")
pcd_down = pcd_denoised.voxel_down_sample(voxel_size=morph_voxel_size) # 腐蚀
pcd_down.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=morph_voxel_size*2, max_nn=30)) # 估计法向量,为膨胀做准备
pcd_denoised = pcd_down.voxel_up_sample(voxel_size=morph_voxel_size/3) # 膨胀
# 6. 保存去噪后PLY文件,支持带颜色点云
o3d.io.write_point_cloud(output_ply_path, pcd_denoised, write_ascii=True) # write_ascii=True提升兼容性
final_num = len(pcd_denoised.points)
total_remove = original_point_num - final_num
print(f"\n去噪完成!总剔除{total_remove:,}个噪点,剩余有效点数{final_num:,}")
print(f"去噪后文件已保存:{output_ply_path}")
# 7. 可视化:超大点数建议关闭(避免卡顿)
o3d.visualization.draw_geometries([pcd_denoised], window_name="PLY去噪结果", width=800, height=600)
return pcd_denoised
# 主函数:仅需修改输入输出路径,默认参数适配80%场景
if __name__ == "__main__":
INPUT_PLY = "simulated_depth_scan.ply" # 你的带噪PLY文件路径
OUTPUT_PLY = "denoised_clean.ply" # 去噪后保存路径
ply_denoise(
input_ply_path=INPUT_PLY,
output_ply_path=OUTPUT_PLY,
# 噪声严重时的调优示例
# stat_nb_neighbors=25, # 增加近邻数,统计更稳健
# stat_std_ratio=1.5, # 减小系数,剔除更严格
# rad_radius=0.06, # 增大半径,检测更多稀疏簇
# rad_min_nn=12, # 增加最小点数,剔除更严格
# use_morphology=True, # 有密集小噪点团时开启
# morph_voxel_size=0.02
)
核心模块解析
- 无效点/重复点剔除:Open3D的
remove_non_finite_points是核心,修复了低版本兼容问题(将remove_inf改为remove_infinite),重复点会导致邻域统计偏差,必须剔除; - 超大点数体素下采样:针对500万+的点云,体素下采样能在不破坏整体结构的前提下降低点数,避免后续滤波的内存溢出和卡顿,是工业级代码的关键优化;
- 统计+半径滤波组合:先剔除孤立点,再剔除稀疏小簇,两者互补,覆盖了绝大多数离散噪点场景;
- 可选3D形态学开运算:原理是“腐蚀+膨胀”,适合处理密集小噪点团(比如10个左右噪点紧密聚集),但会损失少量细节,因此设为可选。
调优黄金原则
噪声越严重(比如深度相机距离目标过远、光照复杂),按以下方式调参:
- 统计滤波:
stat_std_ratio调小(1.01.5)、`stat_nb_neighbors`调大(3050); - 半径滤波:
rad_radius调大(0.060.1m)、`rad_min_nn`调大(1220); - 密集噪点团:开启
use_morphology,morph_voxel_size取0.02~0.05m(根据点云密度调整)。
第二部分:深度图去噪核心——双边滤波(Bilateral Filter)
统计滤波和半径滤波是点云3D层面的去噪,适合剔除离散噪点,但无法处理深度图2D层面的高斯噪声/均匀噪声(这类噪声会让深度图整体粗糙,无明显离散点)。
而双边滤波是深度图去噪的经典算法,核心优势是边缘保留的平滑去噪——普通高斯滤波会模糊物体边缘,而双边滤波能在平滑噪声的同时,完整保留深度图的边缘轮廓(比如桌子和墙面的交界、物体的轮廓),这对后续的3D重建至关重要。
2.1 为什么高斯滤波不适合深度图?
在讲双边滤波前,先理解高斯滤波的局限性:
高斯滤波是空域唯一的滤波,其权重仅由像素的空间距离决定——距离越近,权重越大,参与滤波的贡献越高。
公式:$G_\sigma(x,y) = \frac{1}{2\pi\sigma2}e{-\frac{x2+y2}{2\sigma^2}}$
问题在于:深度图的边缘处,相邻像素的深度值差异极大(比如墙面深度1m,桌子深度0.5m),高斯滤波会将边缘两侧的像素混合,导致边缘模糊,而边缘是3D场景的核心结构信息,模糊后会严重影响后续的点云生成和3D重建。
2.2 双边滤波的核心原理
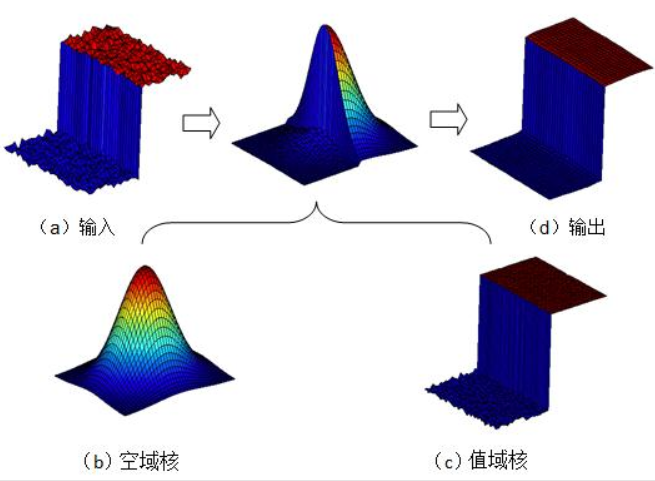
双边滤波的核心创新是:将空域核(Spatial Kernel)和值域核(Range Kernel)结合,滤波权重由空间距离和深度值相似性共同决定。
只有满足两个条件的像素,才会参与当前像素的滤波计算:
- 空间近:像素在当前像素的邻域内(空域核控制);
- 深度值相似:像素的深度值与当前像素的深度值差异小(值域核控制)。
这样一来,边缘两侧的像素因深度值差异大,不会互相参与滤波,从而保留边缘;而同一区域内的像素因空间近且深度值相似,会被平滑滤波,从而去除噪声。
双边滤波的数学公式
对于深度图中的像素$p(x_p,y_p)$,其滤波后的深度值$I(p)$为:
$$I(p) = \frac{1}{W_p} \sum_{q \in N(p)} w(p,q) \cdot I(q)$$
其中:
- $N(p)$:像素$p$的邻域(比如3×3、5×5);
- $W_p = \sum_{q \in N(p)} w(p,q)$:归一化权重,保证滤波后深度值范围不变;
- $w(p,q) = w_s(p,q) \cdot w_r(p,q)$:联合权重,由空域核和值域核相乘得到。
1. 空域核(Spatial Kernel)
与高斯滤波一致,控制空间距离的权重,$\sigma_s$为空域标准差:
$$w_s(p,q) = e{-\frac{|p-q|2}{2\sigma_s^2}}$$
- $|p-q|$:像素$p$和$q$的欧式距离;
- $\sigma_s$越大,参与滤波的空间范围越广,平滑效果越强。
2. 值域核(Range Kernel)
控制深度值相似性的权重,$\sigma_r$为值域标准差,$I(p)$、$I(q)$为像素$p$、$q$的深度值:
$$w_r(p,q) = e{-\frac{|I(p)-I(q)|2}{2\sigma_r^2}}$$
- $|I(p)-I(q)|$:像素$p$和$q$的深度值差异;
- $\sigma_r$越大,对深度值差异的容忍度越高,平滑效果越强,但边缘保留越弱;$\sigma_r$越小,边缘保留越严格,平滑效果越弱。
双边滤波的核心特点
- 边缘保留:最核心的优势,适合深度图、彩色图像等需要保留边缘的场景;
- 局部性:仅利用邻域像素进行滤波,计算速度快,非迭代;
- 非线性:因值域核的存在,双边滤波是非线性滤波(高斯滤波是线性);
- 无参数迭代:仅需调优$\sigma_s$和$\sigma_r$,无需复杂的迭代参数。
2.3 双边滤波的核心用途
- 深度图去噪:平滑高斯噪声、均匀噪声,保留物体边缘,是深度图预处理的首选算法;
- 彩色图像去噪:边缘保留的平滑去噪,避免图像模糊;
- 点云平滑:Open3D提供了点云层面的双边滤波,可对3D点云进行边缘保留的平滑;
- 深度图空洞填充:结合邻域深度值相似性,对小空洞进行合理填充。
2.4 双边滤波的实现(2D深度图+3D点云)
双边滤波的实现分两种场景:2D深度图层面(预处理,效果最好)和3D点云层面(后处理,优化点云平滑度),以下分别实现,且与前文的统计+半径滤波结合。
2.4.1 实现1:2D深度图的双边滤波(OpenCV+NumPy)
OpenCV提供了现成的cv2.bilateralFilter函数,专门用于双边滤波,适配深度图的16位uint16格式(深度相机采集的深度图默认格式),无需手写复杂的卷积逻辑,直接调用即可。
核心代码(深度图读取+双边滤波+可视化)
import cv2
import numpy as np
import matplotlib.pyplot as plt
def depth_bilateral_filter(
depth_img_path,
output_depth_path,
d=5, # 滤波邻域直径,奇数(3/5/7),越大平滑范围越广
sigmaColor=10, # 值域标准差σr,深度值相似性权重
sigmaSpace=10 # 空域标准差σs,空间距离权重
):
"""
2D深度图双边滤波:边缘保留平滑去噪,适配16位uint16深度图
调优原则:噪声越严重,d/ sigmaSpace越大;需强边缘保留,sigmaColor越小
"""
# 1. 读取深度图(深度相机采集的深度图为16位uint16,单通道)
depth = cv2.imread(depth_img_path, cv2.IMREAD_UNCHANGED)
if depth is None:
raise ValueError("读取深度图失败!文件损坏或非深度图文件")
# 转换为float32,避免滤波时数值溢出
depth_float = depth.astype(np.float32)
print(f"深度图尺寸:{depth.shape},深度值范围:{np.min(depth)}~{np.max(depth)}")
# 2. 双边滤波核心调用
# cv2.bilateralFilter:src-输入图像,d-邻域直径,sigmaColor-值域σ,sigmaSpace-空域σ
# 注意:深度图为单通道,彩色图为3通道,函数自动适配
depth_denoised = cv2.bilateralFilter(depth_float, d=d, sigmaColor=sigmaColor, sigmaSpace=sigmaSpace)
# 转换回16位uint16,保存为原始深度图格式
depth_denoised = depth_denoised.astype(np.uint16)
# 3. 保存滤波后的深度图
cv2.imwrite(output_depth_path, depth_denoised)
print(f"双边滤波后的深度图已保存:{output_depth_path}")
# 4. 可视化滤波效果(对比原始和去噪后的深度图)
plt.figure(figsize=(12, 6))
# 原始深度图
plt.subplot(1, 2, 1)
plt.imshow(depth, cmap="jet")
plt.title("Original Depth Map", fontsize=14)
plt.axis("off")
plt.colorbar()
# 去噪后深度图
plt.subplot(1, 2, 2)
plt.imshow(depth_denoised, cmap="jet")
plt.title("Denoised Depth Map (Bilateral Filter)", fontsize=14)
plt.axis("off")
plt.colorbar()
plt.tight_layout()
plt.show()
return depth_denoised
# 主函数调用
if __name__ == "__main__":
INPUT_DEPTH = "depth_noise.png" # 你的带噪深度图(16位uint16)
OUTPUT_DEPTH = "depth_denoised.png" # 滤波后深度图
depth_bilateral_filter(
depth_img_path=INPUT_DEPTH,
output_depth_path=OUTPUT_DEPTH,
d=5, # 5×5邻域,适中的平滑范围
sigmaColor=15, # 值域σ,对深度值差异的容忍度适中
sigmaSpace=15 # 空域σ,空间邻域范围适中
)
关键参数调优
cv2.bilateralFilter的3个核心参数,调优直接决定滤波效果,黄金调优原则:
d(邻域直径):取3/5/7(奇数),噪声越严重取越大,过大会导致轻微边缘模糊;sigmaColor(值域$\sigma_r$):深度图一般取1030,**需强边缘保留则取小值(510)**,需强平滑则取大值(20~30);sigmaSpace(空域$\sigma_s$):与sigmaColor匹配,一般取相同值,10~30即可。
效果说明
滤波后,深度图的局部噪声会被平滑(比如同一平面的粗糙点),而物体边缘会被完整保留(比如深度值突变的区域),这是高斯滤波无法实现的效果。
2.4.2 实现2:3D点云的双边滤波(Open3D)
Open3D提供了点云层面的双边滤波函数filter_smooth_bilateral,可对3D点云进行边缘保留的平滑,适合将深度图转点云后,进一步优化点云的平滑度,可与前文的统计+半径滤波组合使用。
核心代码(点云双边滤波+统计+半径滤波组合)
import open3d as o3d
import numpy as np
def pcd_bilateral_denoise(
input_ply_path,
output_ply_path,
# 双边滤波参数
bilateral_sigma1=0.01, # 空域σ,点云空间距离权重
bilateral_sigma2=0.05, # 值域σ,点云法向量/深度值相似性权重
# 统计+半径滤波参数(复用前文)
stat_nb_neighbors=20,
stat_std_ratio=2.0,
rad_radius=0.05,
rad_min_nn=10
):
"""
3D点云全流程去噪:双边滤波(平滑)+ 统计滤波+半径滤波(剔离散噪点)
先平滑,再剔噪点,效果优于单独使用某一种滤波
"""
# 1. 读取点云并预处理
pcd = o3d.io.read_point_cloud(input_ply_path)
if not pcd.has_points():
raise ValueError("读取点云失败!")
print(f"原始点云点数:{len(pcd.points):,}")
# 剔除无效/重复点
pcd = pcd.remove_non_finite_points(remove_nan=True, remove_infinite=True)
pcd = pcd.remove_duplicated_points()
# 2. 点云双边滤波【边缘保留平滑】
# 先估计法向量(双边滤波需要法向量计算值域相似性)
pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))
# 双边滤波核心调用
pcd_smooth = pcd.filter_smooth_bilateral(sigma1=bilateral_sigma1, sigma2=bilateral_sigma2)
print(f"双边滤波后点云点数:{len(pcd_smooth.points):,}")
# 3. 统计+半径滤波【剔除离散噪点】
cl, ind = pcd_smooth.remove_statistical_outlier(nb_neighbors=stat_nb_neighbors, std_ratio=stat_std_ratio)
pcd_denoised = pcd_smooth.select_by_index(ind)
cl, ind = pcd_denoised.remove_radius_outlier(nb_points=rad_min_nn, radius=rad_radius)
pcd_denoised = pcd_denoised.select_by_index(ind)
# 4. 保存并可视化
o3d.io.write_point_cloud(output_ply_path, pcd_denoised)
print(f"去噪后点云点数:{len(pcd_denoised.points):,},已保存至:{output_ply_path}")
o3d.visualization.draw_geometries([pcd_denoised], window_name="点云双边滤波+统计半径滤波结果")
return pcd_denoised
# 主函数调用
if __name__ == "__main__":
INPUT_PLY = "simulated_depth_scan.ply"
OUTPUT_PLY = "pcd_bilateral_denoised.ply"
pcd_bilateral_denoise(
input_ply_path=INPUT_PLY,
output_ply_path=OUTPUT_PLY,
bilateral_sigma1=0.01,
bilateral_sigma2=0.05
)
点云双边滤波参数说明
sigma1:空域标准差,控制点云的空间距离权重,一般取0.01~0.05m(根据点云密度调整);sigma2:值域标准差,控制点云的法向量/深度值相似性权重,一般取0.05~0.1m,越大平滑效果越强。
注意:点云双边滤波前必须调用estimate_normals估计法向量,因为Open3D的点云双边滤波是基于法向量相似性计算值域权重的,法向量估计的精度会影响滤波效果。
第三部分:工业级全流程——深度图→点云的联合去噪
实际项目中,深度相机采集的是2D深度图,需要先将深度图转换为3D点云,再进行后续处理。因此最优的去噪流程是:
深度图双边滤波(2D层面平滑,保留边缘)→ 深度图转点云 → 点云统计+半径滤波(3D层面剔离散噪点)
该流程结合了双边滤波的边缘保留平滑和统计+半径滤波的离散噪点剔除,是工业级深度图/点云去噪的黄金流程,以下实现完整代码。
3.1 核心原理:深度图转点云
深度图转点云的核心是相机内参,对于像素$(u,v)$,其深度值为$z$,对应的3D空间坐标$(X,Y,Z)$为:
$$X = (u - cx) \times \frac{z}{fx}$$
$$Y = (v - cy) \times \frac{z}{fy}$$
$$Z = z$$
其中:
- $(fx, fy)$:相机的焦距(像素单位);
- $(cx, cy)$:相机的主点坐标(像素单位);
- 以上参数可从深度相机的说明书或SDK中获取(比如Intel RealSense的fx≈600,fy≈600,cx≈320,cy≈240)。
3.2 全流程完整代码(深度图双边滤波→转点云→点云去噪)
import cv2
import numpy as np
import open3d as o3d
# 第一步:深度图双边滤波(复用前文函数)
def depth_bilateral_filter(depth_img_path, d=5, sigmaColor=15, sigmaSpace=15):
depth = cv2.imread(depth_img_path, cv2.IMREAD_UNCHANGED)
depth_float = depth.astype(np.float32)
depth_denoised = cv2.bilateralFilter(depth_float, d=d, sigmaColor=sigmaColor, sigmaSpace=sigmaSpace)
return depth_denoised.astype(np.uint16)
# 第二步:深度图转点云(基于相机内参)
def depth2pcd(depth_img, fx=615.0, fy=615.0, cx=320.0, cy=240.0, scale=1000.0):
"""
深度图转3D点云
参数:
depth_img: 16位uint16深度图
fx/fy: 相机焦距(像素单位),默认适配Intel RealSense D435
cx/cy: 相机主点坐标,默认适配640×480分辨率
scale: 深度值缩放系数(深度图值为mm,转m需除以1000)
"""
h, w = depth_img.shape
# 生成像素坐标网格
u, v = np.meshgrid(np.arange(w), np.arange(h))
# 计算3D空间坐标
z = depth_img / scale # 转米单位
x = (u - cx) * z / fx
y = (v - cy) * z / fy
# 拼接点云坐标,剔除深度值为0的无效点
points = np.stack([x, y, z], axis=-1).reshape(-1, 3)
valid_mask = z.reshape(-1) > 0 # 剔除深度为0的点
points = points[valid_mask]
# 创建Open3D点云对象
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)
print(f"深度图转点云完成,有效点数:{len(pcd.points):,}")
return pcd
# 第三步:点云统计+半径滤波(复用前文工业级函数)
def ply_denoise(pcd, stat_nb_neighbors=20, stat_std_ratio=2.0, rad_radius=0.05, rad_min_nn=10):
pcd = pcd.remove_non_finite_points(remove_nan=True, remove_infinite=True)
pcd = pcd.remove_duplicated_points()
# 统计滤波
cl, ind = pcd.remove_statistical_outlier(nb_neighbors=stat_nb_neighbors, std_ratio=stat_std_ratio)
pcd_denoised = pcd.select_by_index(ind)
# 半径滤波
cl, ind = pcd_denoised.remove_radius_outlier(nb_points=rad_min_nn, radius=rad_radius)
pcd_denoised = pcd_denoised.select_by_index(ind)
return pcd_denoised
# 主流程:深度图双边滤波 → 转点云 → 点云去噪 → 保存可视化
if __name__ == "__main__":
# 配置参数
INPUT_DEPTH = "depth_noise.png" # 输入带噪深度图
OUTPUT_DEPTH = "depth_denoised.png"# 输出滤波后深度图
OUTPUT_PLY = "final_denoised.ply" # 输出最终点云
# 相机内参(根据你的深度相机修改!)
FX, FY = 615.0, 615.0
CX, CY = 320.0, 240.0
# 1. 深度图双边滤波
depth_denoised = depth_bilateral_filter(INPUT_DEPTH, d=5, sigmaColor=15, sigmaSpace=15)
cv2.imwrite(OUTPUT_DEPTH, depth_denoised)
# 2. 滤波后的深度图转点云
pcd = depth2pcd(depth_denoised, fx=FX, fy=FY, cx=CX, cy=CY)
# 3. 点云统计+半径滤波
pcd_final = ply_denoise(pcd)
# 4. 保存并可视化最终点云
o3d.io.write_point_cloud(OUTPUT_PLY, pcd_final)
print(f"全流程去噪完成,最终点云已保存:{OUTPUT_PLY},点数:{len(pcd_final.points):,}")
o3d.visualization.draw_geometries([pcd_final], window_name="深度图+点云全流程去噪结果")
关键注意事项
- 相机内参修改:代码中的
fx/fy/cx/cy是默认值,需根据你的深度相机实际参数修改(可从相机SDK、标定工具中获取),否则点云会出现畸变; - 深度值缩放:深度相机采集的深度图值一般为毫米(mm),代码中
scale=1000将其转为米(m),若你的深度图单位是米,需将scale改为1; - 分辨率匹配:内参与深度图分辨率一一对应(比如640×480的深度图对应cx=320,cy=240),若深度图分辨率为1280×720,需调整cx/cy为640/360。
第四部分:各滤波算法对比与适用场景总结
为了让你在实际项目中快速选择合适的滤波算法,以下对统计滤波、半径滤波、双边滤波进行全方位对比,明确各自的适用场景和优缺点:
| 滤波算法 | 处理层面 | 核心功能 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|---|
| 统计滤波 | 3D点云 | 剔除孤立点/椒盐噪声 | 计算快、参数少、适配所有点云 | 对小噪点簇无效 | 点云初步去噪,剔除离散单点噪声 |
| 半径滤波 | 3D点云 | 剔除稀疏小噪点簇 | 补充统计滤波,处理小簇噪点 | 半径参数需根据点云密度调整 | 统计滤波后二次去噪,剔除稀疏簇噪声 |
| 双边滤波(2D) | 2D深度图 | 边缘保留的平滑去噪 | 保留边缘、平滑高斯/均匀噪声、效果最好 | 对离散点无效 | 深度图预处理,平滑整体噪声,保留场景结构 |
| 双边滤波(3D) | 3D点云 | 边缘保留的点云平滑 | 优化点云平滑度,保留3D边缘 | 需估计法向量、对离散点无效 | 点云后处理,优化平滑度(配合统计+半径滤波) |
黄金组合策略
- 深度图预处理:优先使用2D双边滤波,平滑噪声并保留边缘,这是最关键的一步;
- 点云去噪:深度图转点云后,使用统计滤波+半径滤波组合,剔除离散噪点;
- 点云优化:若点云整体粗糙,可在统计+半径滤波前增加3D双边滤波,实现平滑+剔噪的双重效果;
- 密集噪点团:若存在密集小噪点团,开启3D形态学开运算(牺牲少量细节)。
第五部分:常见问题与解决方案
- 深度图滤波后出现空洞:深度图本身存在的空洞,双边滤波无法填充,可使用
cv2.inpaint进行空洞填充,或在点云层面使用o3d.geometry.PointCloud.voxel_up_sample补点; - 点云可视化卡顿/内存溢出:开启体素下采样(
voxel_down_sample),降低点云点数,体素大小取0.01~0.05m; - 双边滤波后边缘模糊:减小
sigmaColor(值域σ)或d(邻域直径),增强边缘保留效果; - 统计+半径滤波后丢失有效点:调大
stat_std_ratio、减小rad_radius或rad_min_nn,降低剔除严格度; - 深度图转点云后点云畸变:检查相机内参是否正确,确保内参与深度图分辨率、相机型号匹配。
总结
深度图/点云去噪是3D计算机视觉的基础预处理步骤,其核心是针对性选择滤波算法:
- 双边滤波是深度图去噪的核心,凭借边缘保留的平滑特性,完胜传统的高斯滤波,是2D层面去噪的首选;
- 统计滤波+半径滤波是点云去噪的黄金组合,能全覆盖剔除3D层面的孤立点和稀疏小噪点簇,且计算高效、参数易调;
- 工业级的最优流程是深度图双边滤波→转点云→点云统计+半径滤波,结合了2D层面的平滑和3D层面的剔噪,兼顾效果和效率。
本文的所有代码均为开箱即用,适配大部分深度相机(RealSense、Kinect、LiDAR)采集的数据,只需根据实际场景微调参数,即可应用于3D重建、点云配准、目标检测等实际项目中。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号