2026年美赛C题——翻译及建模思路

#

《与星共舞》是一档国际电视节目 IP 的美国版，原版为英国经典节目《舞动奇迹》（前身为《欢乐起舞》）。该节目的改编版本已在阿尔巴尼亚、阿根廷、澳大利亚、中国、法国、印度等多个国家推出。本次问题的研究核心为该节目的美国版，目前该版本已完成 34 季的播出。

节目中，明星嘉宾会与专业舞者组成搭档，每周进行舞蹈表演。专业评委团会为每组搭档的表演打分，观众则可通过电话或线上渠道，为自己当周喜爱的搭档投票。观众每周可投票一次或多次，投票次数不设限但不得超过节目组当周公布的上限。此外，观众投票仅能为希望留任的明星助力，无法直接投票淘汰某位明星。节目组会结合评委打分与观众投票的结果，决出当周需要淘汰的搭档 —— 即综合得分最低的一组。最终会有三组搭档晋级总决赛（部分赛季的晋级名额更多），总决赛当周，节目组将依据观众投票与评委打分的综合得分，为晋级搭档排出冠亚季军（或前四、前五名）。

评委打分与观众投票的结果融合方式有多种。该节目美国版前两季采用排名法结合两项结果，而第二季的一起争议事件（知名球星杰瑞・莱斯尽管评委打分常年偏低，却仍晋级总决赛），促使节目组对融合规则做出调整，改用百分比法替代排名法。这两种计算方式的具体示例见附录。

第二十七季，节目再度引发争议：名人选手鲍比・博恩斯虽评委打分始终处于低位，却最终夺冠。为回应此次争议，从第二十八季开始，节目组对淘汰流程稍作修改：先根据评委打分与观众投票的综合结果选出排名末两位的搭档，再在直播节目中由评委投票决定淘汰其中哪一组。大约在同一季，制作方还恢复了前两季采用的排名法，将评委打分与观众投票结果结合。这一规则调整的具体赛季尚无确切记载，但合理推测为第二十八季。

评委打分本应客观体现舞者的专业技术水平，但其评判标准仍存在一定的主观性。观众投票的主观性则更强，投票倾向不仅受舞蹈表演质量的影响，还与明星嘉宾的人气和个人魅力密切相关。事实上，节目组在一定程度上更乐见评委与观众的意见、投票结果出现分歧，因为这类争议能大幅提升观众的关注与参与热情。

本文提供了含评委打分与选手信息的相关数据，并附具体说明。你可自行决定是否补充其他信息或数据，但所有数据来源均需完整标注。请基于该数据完成以下研究任务：

在这里插入图片描述

  1. 构建数学模型（单个或多个），估算每位选手在其参赛各周的观众投票数（该数据未对外公开，属于节目组严格保密的核心信息）。
    • 你所构建的模型，其估算的观众投票数能否推导出与节目每周淘汰结果一致的结论？请给出一致性度量指标。
    • 你估算出的观众投票总数的置信度如何？该置信度是否对所有选手、所有比赛周均保持一致？请为估算结果提供置信度度量指标。
  2. 将观众投票的估算结果与其余数据结合，开展以下分析：
    • 对比分析节目采用的两种票分融合方式（排名法、百分比法）在各季应用后的比赛结果（即对每一季同时应用这两种融合方法）。若不同方法得出的结果存在差异，是否其中一种方法更偏向观众投票的结果？
    • 针对存在争议的知名选手（即评委打分与观众投票结果存在明显分歧的选手），分析上述两种票分融合方式的应用效果：票分融合方式的选择，是否会让每位争议选手得到相同的比赛结果？若新增 “由评委从排名末两位的搭档中决定淘汰对象” 这一规则，会对比赛结果产生何种影响？你可参考以下争议选手案例（也可选用你研究中发现的其他案例）：▪ 第二季的杰瑞・莱斯：连续 5 周评委打分垫底，却最终获得亚军。▪ 第四季的比利・雷・塞勒斯：连续 6 周评委打分倒数第一，最终位列第五。▪ 第十一季的布里斯托尔・佩林：12 次评委打分排名最低，仍拿下季军。▪ 第二十七季的鲍比・博恩斯：评委打分始终处于低位，却最终夺冠。
    • 基于你的全部分析结果，为节目后续季数推荐适用的票分融合方式并说明核心原因；是否建议节目组增设 “由评委从排名末两位的搭档中决定淘汰对象” 这一规则？
  3. 结合包含观众投票估算结果的完整数据集，构建模型分析不同专业舞者、以及数据中可提取的明星特质（年龄、所属行业等）对明星比赛成绩的影响程度：这些因素对明星的比赛表现影响有多大？其对评委打分和观众投票的影响方式是否一致？
  4. 设计一套全新的周度票分融合体系，将观众投票与评委打分结合，且你认为该体系更具 “公平性”（或在其他维度更优，如大幅提升节目对观众的吸引力）。请详细论证该体系为何值得节目制作方采纳。
  5. 撰写一份总页数不超过 25 页的研究报告，报告中需包含 1-2 页的备忘录，总结研究核心结果，并为《与星共舞》制作方分析票分融合方式对比赛的影响，同时给出未来季数的票分融合方式建议。

©2026 美国数学建模竞赛组委会 | 官网：www.comap.org | 建模竞赛官网：www.mathmodels.org | 邮箱：info@comap.org

你提交的 PDF 版解题方案需满足总页数不超过 25 页，且包含以下内容：

  • 1 页摘要页
  • 目录
  • 完整的解题方案
  • 1-2 页备忘录
  • 参考文献
  • AI 使用报告（若使用了 AI 工具，该报告不计入 25 页的页数限额）

注意事项

：本次美国数学建模竞赛的参赛作品无明确最低页数要求；25 页的页数限额可用于所有解题内容，以及你希望补充的各类信息（如示意图、图表、计算过程、数据表格等），赛事方接受部分解题方案。允许参赛者谨慎使用 ChatGPT 等生成式 AI 工具（并非完成解题方案的必需工具）；若选择使用，参赛者必须遵守美国数学建模竞赛组委会的 AI 使用政策，且需在 PDF 版解题方案的末尾附加 AI 使用报告，该报告不计入 25 页的解题内容限额。

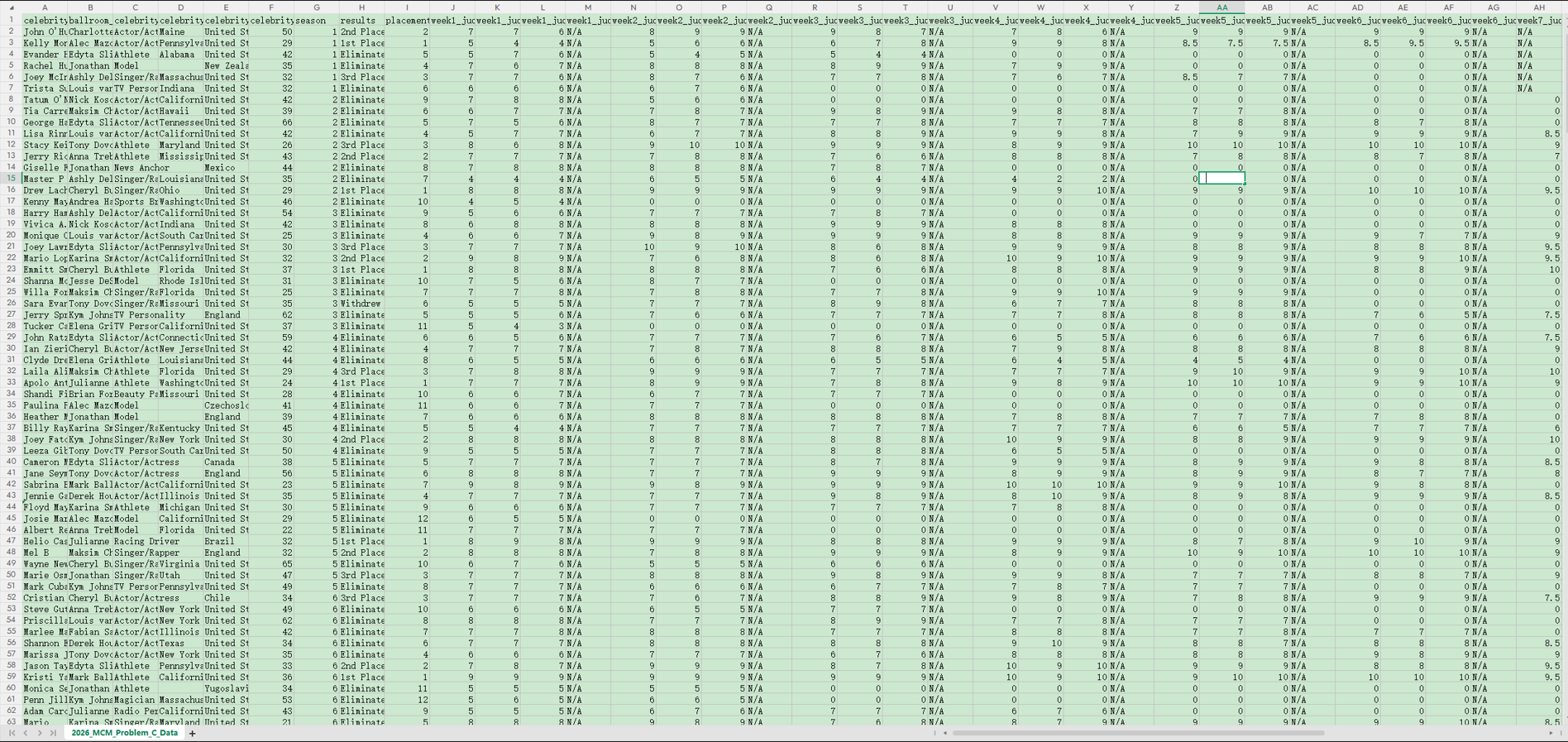
数据文件

：2026_MCM_Problem_C_Data.csv文件包含《与星共舞》第 1 至 34 季的选手信息、比赛结果及各周评委打分数据，数据详细说明见表 1。

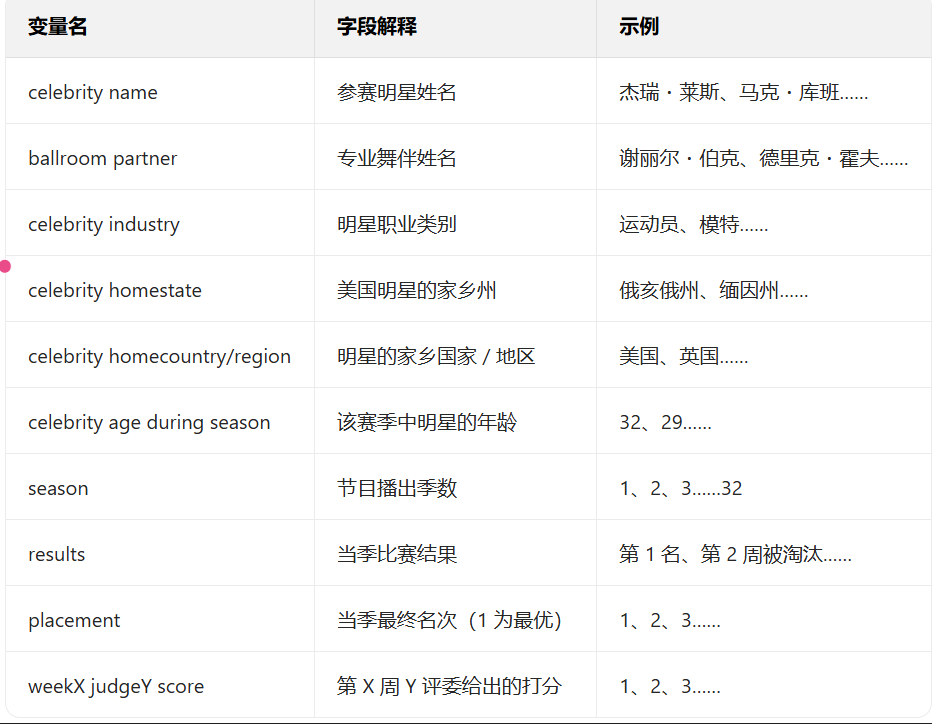
在这里插入图片描述

      表 1：2026_MCM_Problem_C_Data.csv 数据集字段说明

数据说明

  1. 每支舞蹈的评委打分范围为 1 分（最低） 至 10 分（最高）。a. 部分周次的公示分数包含小数（如 8.5），原因是该明星当周表演了多支舞蹈，公示分数为各舞蹈得分的平均值。b. 部分周次会设置额外加分（如舞蹈对决环节），这些加分将平均分配到对应评委 / 舞蹈的得分中。c. 团体舞蹈的得分会与每位团队成员的个人得分进行平均合并。
  2. 评委按其为舞蹈打分的顺序排列；因此，“评委 Y” 在不同周次或不同赛季可能并非同一人。
  3. 各赛季的参赛明星人数、节目播出周数均不相同。
  4. 第 15 季是唯一一季采用全明星阵容的赛季，所有参赛明星均为往届回归选手。
  5. 偶尔会出现单周无明星淘汰，或单周淘汰多名明星的情况。
  6. 数据集中的 “N/A” 值出现场景：a. 若当周无第 4 位评委（通常为 3 位评委），则第 4 位评委的得分记为 N/A；b. 若某赛季未播出对应周次（例如第 1 季仅播出 6 周，因此第 7 至 11 周的得分均记为 N/A）。
  7. 已被淘汰的明星后续周次得分记为 0。例如，第 1 季中首位被淘汰的明星是特里斯塔・萨特（Trista Sutter），她在第 2 周节目结束后被淘汰，因此该赛季剩余周次（第 3 至 6 周）的得分均记为 0。
选手 评委总分 评委排名 **观众投票数 *** **观众投票排名 *** 排名总和
蕾切尔・亨特（Rachel Hunter） 25 2 110 万 4 6
乔伊・麦金泰尔（Joey McIntyre） 20 4 370 万 1 5
约翰・奥赫利（John O’Hurley） 21 3 320 万 2 5
凯莉・莫纳科（Kelly Monaco） 26 1 200 万 3 4 
                                   表 2：按排名融合评委打分与观众投票的示例（第 1 季第 4 周）

从第 3 季开始，节目组改用百分比法替代排名法来融合评委打分与观众投票。我们以第 5 季第 9 周的比赛为例进行说明：该周珍妮・加思（Jennie Garth）被淘汰。同样，我们通过人工生成一组观众投票数据，使得最终的百分比融合结果与实际淘汰结果一致。

具体计算逻辑为：

  • 评委得分占比：将该选手的评委总分，除以当期所有 4 位选手的评委总分之和。
  • 仅按评委得分占比排名时，珍妮位列第 3；但在加入我们人工设定的 1000 万观众投票的占比后，她的综合占比排名降至第 4，从而触发淘汰。
选手 评委总分 评委得分占比 **观众投票数 *** **观众投票占比 *** 占比总和
珍妮・加思（Jennie Garth） 29 29/117 = 24.8% 110 万 1.1/10 = 11% 35.8
玛丽・奥斯蒙德（Marie Osmond） 28 28/117 = 23.9% 370 万 3.7/10 = 37% 60.9
梅尔・B（Mel B） 30 30/117 = 25.6% 320 万 3.2/10 = 32% 57.8
埃利奥・卡斯特罗内维斯（Helio Castroneves） 30 30/117 = 25.6% 200 万 2/10 = 20% 45.6
总计 117 — 1000 万 — — 
                                表 3：按百分比融合评委打分与观众投票的示例（第 5 季第 9 周）
  • 注：观众投票数为未知数据，表中数值为假设值，仅用于推导出符合最终排名的结果。

1. 估算观众投票数（含一致性与置信度验证）

基础思路：用已知的淘汰结果和评委得分，反向推导满足融合规则的观众投票数范围。

基础模型：线性不等式组（约束为融合规则）、蒙特卡洛模拟（评估置信度）

完成步骤：

  1. 按周提取评委得分和淘汰结果
  2. 对每周构建融合规则的约束方程
  3. 求解可行的观众投票区间
  4. 用蒙特卡洛模拟计算一致性准确率和置信区间

2. 对比两种票分融合方式 + 争议选手分析 + 方法推荐

基础思路：用估算的观众投票数分别代入两种规则，对比结果差异，分析争议选手的敏感性。

基础模型：假设检验（比较结果差异）、敏感性分析（测试规则对争议选手的影响）

完成步骤：

  1. 对每一季分别应用排名 / 百分比法
  2. 统计两种方法的淘汰 / 晋级差异率
  3. 针对争议选手，测试规则变化对其结果的影响
  4. 结合公平性和娱乐性给出推荐

3. 分析专业舞者与明星特质的影响

基础思路：构建回归模型，量化各因素对评委打分和观众投票的独立影响。

基础模型：多元线性回归（或混合效应模型）、相关性分析

完成步骤：

  1. 提取明星特质（年龄、行业等）和专业舞者信息
  2. 分别对评委得分和估算的观众投票数做回归
  3. 比较系数大小和显著性
  4. 解释影响差异

4. 设计更优的票分融合体系

基础思路：平衡评委专业性与观众参与度，引入动态权重或保底机制，提升公平性和观赏性。

基础模型：加权融合模型（权重动态调整）、博弈论模型（平衡各方利益）

完成步骤：

  1. 定义 “公平 / 精彩” 的量化指标
  2. 设计融合公式（如评委得分加权 + 观众投票加权 + 争议修正项）
  3. 用历史数据验证新规则的效果
  4. 论证其优势

5. 撰写竞赛报告与备忘录

基础思路：按 MCM 竞赛要求结构，突出模型创新、结果清晰、建议可行。

基础模型：结构化报告框架（摘要→目录→模型→结果→建议→备忘录）

完成步骤：

  1. 整理各部分结果，提炼核心结论
  2. 撰写 1 页摘要和 1-2 页备忘录
  3. 按逻辑组织内容，控制页数在 25 页内
  4. 补充参考文献和 AI 使用报告
posted @ 2026-01-30 10:50  TTGF  阅读(1778)  评论(0)    收藏  举报