具身智能：零基础入门睿尔曼机械臂（五）—— 手眼标定核心原理与数学求解

前言
一、相关概念阐述
二、手眼标定原理解释
- 2.1 Eye-in-Hand（眼在手上）系统原理
- 2.2 Eye-to-Hand（眼在手外）系统原理
三、数学推演：AX=XB方程的求解
四、实际应用与操作指南

前言

在机器人与计算机视觉的交叉领域，精确的空间坐标映射是实现机械臂与环境高效交互的核心前提。想象这样一个场景：工业机器人需要从传送带上抓取随机摆放的零件，或是服务机器人要精准拾取用户指定的物品——相机作为“眼睛”能识别目标的位置，但机械臂作为“手”却只理解自身坐标系下的指令。如何让“眼”看到的信息准确传递给“手”？手眼标定正是解决这一问题的关键技术。
手眼标定的本质是建立相机坐标系与机械臂坐标系之间的刚性变换关系，通过这一关系，可将相机检测到的目标坐标实时转换为机械臂能够执行的运动指令。无论是工业生产中的自动化抓取、精密装配，还是科研领域的视觉伺服控制、动态环境交互，手眼标定都扮演着不可或缺的角色。
本文将从基础概念出发，系统拆解手眼标定的两种核心架构（Eye-in-Hand与Eye-to-Hand），深入推导其数学原理，详解AX=XB方程的由来与求解方法，并结合实际应用场景说明标定过程中的关键注意事项，为从事机器人视觉相关工作的开发者和研究者提供一份全面、可落地的技术指南。

一、相关概念阐述

在深入原理之前，我们需要明确手眼标定涉及的核心概念与基础工具，这是理解后续内容的前提。

1.1 核心坐标系定义

手眼标定的本质是坐标系间的变换，需明确以下4个关键坐标系：

机械臂基座坐标系（Base Frame, ${B}$）：机械臂的基准坐标系，固定于机械臂基座，是机械臂运动计算的参考基准，所有关节运动均相对于该坐标系描述。
机械臂末端坐标系（End-effector Frame, ${E}$）：固定于机械臂末端执行器（如夹爪），用于描述末端执行器的实时位姿（位置+姿态），可通过机械臂API直接读取。
相机坐标系（Camera Frame,${C}$）：以相机光心为原点的三维坐标系，X轴与Y轴平行于图像平面，Z轴为相机光轴方向（遵循右手定则），用于描述目标在相机视野中的三维位置。
标定板坐标系（Checkerboard Frame, ${W}$）：固定于标定板（通常为棋盘格）的局部坐标系，原点一般设为标定板左上角角点，用于提供已知的三维特征点，作为坐标变换的“桥梁”。

1.2 齐次变换矩阵

空间中点的位姿（位置+姿态）变换需通过4×4齐次变换矩阵描述，其形式如下：
$$
T = \begin{bmatrix}
R & t \
0^T & 1
\end{bmatrix}
$$
其中：

$R$ 是3×3旋转矩阵，描述两个坐标系间的姿态关系，满足 $R^T R = I$（正交性）和 $\det(R)=1$（右手坐标系）；
$t$ 是3×1平移向量，描述目标坐标系原点相对于参考坐标系的位置；
$0^T = [0,0,0]$，用于保持齐次坐标的数学一致性。
齐次变换矩阵具有复合性：若存在坐标系A→B的变换 $T_{AB}$ 和 B→C的变换 $T_{BC}$，则A→C的变换为 $T_{AC} = T_{AB} \times T_{BC}$（矩阵乘法），这是手眼标定数学推演的核心基础。

1.3 相机内参与外参

手眼标定依赖相机的参数标定结果，需明确内参与外参的区别：

内参（Intrinsic Parameters）：描述相机自身的光学特性，与外部环境无关，包括焦距（$f_x, f_y$）、主点坐标（$c_x, c_y$）、畸变系数（$k_1, k_2, p_1, p_2$ 等）。内参通过张正友标定法等可预先求解，是将相机像素坐标转换为相机坐标系下三维坐标的前提。
外参（Extrinsic Parameters）：描述相机坐标系相对于世界坐标系（此处为标定板坐标系）的变换关系（旋转矩阵 $R_{CW}$ + 平移向量 $t_{CW}$），即 $T_{CW} = \begin{bmatrix} R_{CW} & t_{CW} \ 0^T & 1 \end{bmatrix}$。外参需通过拍摄标定板图像求解，是手眼标定中的关键中间量。

1.4 手眼标定的两种核心架构

根据相机与机械臂的安装关系，手眼标定分为两种典型架构，其标定目标和实现方式存在本质差异：

架构类型	安装方式	核心特点	标定目标
Eye-in-Hand（眼在手上）	相机固定于机械臂末端执行器	相机随机械臂运动，机械臂基座与标定板固定	相机坐标系相对于机械臂末端坐标系的变换 $T_{EC}$（即X）
Eye-to-Hand（眼在手外）	相机固定于机械臂基座或外部支架	相机与机械臂基座固定，标定板固定于机械臂末端	相机坐标系相对于机械臂基座坐标系的变换 $T_{BC}$（即X）

二、手眼标定原理解释

手眼标定的核心逻辑是：通过机械臂的已知运动和相机拍摄的标定板图像，构建坐标系变换的闭合回路，从而建立关于未知变换矩阵X的方程，最终求解X。以下分别针对两种架构详细解析原理。

2.1 Eye-in-Hand（眼在手上）系统原理

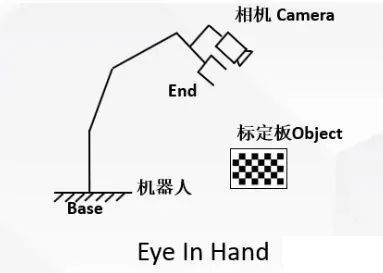
2.1.1 系统结构特点

相机与机械臂末端刚性连接，机械臂运动时相机同步运动；
标定板固定于工作台（与机械臂基座坐标系相对静止）；
已知量：机械臂末端在基座坐标系下的位姿（$T_{BE_1}, T_{BE_2}, ..., T_{BE_n}$）；
可求解量：相机相对于标定板的外参（$T_{CW_1}, T_{CW_2}, ..., T_{CW_n}$）；
未知量：相机与机械臂末端的变换 $T_{EC}$（即X，需标定求解）。

2.1.2 变换回路构建

当机械臂带动相机运动两次，到达两个不同位姿 $E_1$ 和 $E_2$ 时，我们可以构建两个闭合的坐标变换回路：

第一次运动（位姿1）：机械臂基座 → 末端 $E_1$ → 相机 $C_1$ → 标定板 $W$ → 机械臂基座
变换关系：$T_{BW} = T_{BE_1} \times T_{E_1C_1} \times T_{C_1W}$
第二次运动（位姿2）：机械臂基座 → 末端 $E_2$ → 相机 $C_2$ → 标定板 $W$ → 机械臂基座
变换关系：$T_{BW} = T_{BE_2} \times T_{E_2C_2} \times T_{C_2W}$
由于标定板与机械臂基座相对静止，$T_{BW}$ 是固定不变的；同时，相机与机械臂末端刚性连接，$T_{E_1C_1} = T_{E_2C_2} = X$（未知变换矩阵）。因此：
$$ T_{BE_1} \times X \times T_{C_1W} = T_{BE_2} \times X \times T_{C_2W} $$

2.1.3 方程简化（AX=XB形式）

定义两个关键变换：

$A = T_{BE_1}^{-1} \times T_{BE_2}$：机械臂末端从位姿1到位姿2的相对变换（已知，由机械臂API读取的位姿计算）；
$B = T_{C_1W} \times T_{C_2W}^{-1}$：相机坐标系从位姿1到位姿2的相对变换（已知，由两次拍摄的标定板外参计算）。
将上述定义代入变换回路方程，两边左乘 $T_{BE_1}^{-1}$，整理后得到：
$$ X \times B = A \times X $$
即：
$$ A X = X B $$
这就是Eye-in-Hand系统手眼标定的核心方程，求解该方程即可得到相机与机械臂末端的变换矩阵X。

2.2 Eye-to-Hand（眼在手外）系统原理

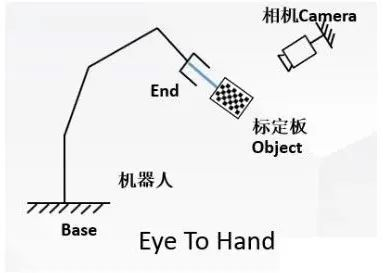
2.2.1 系统结构特点

相机固定于机械臂基座或外部支架（与基座坐标系相对静止）；
标定板与机械臂末端刚性连接，机械臂运动时标定板同步运动；
已知量：机械臂末端在基座坐标系下的位姿（$T_{BE_1}, T_{BE_2}, ..., T_{BE_n}$）；
可求解量：相机相对于标定板的外参（$T_{CW_1}, T_{CW_2}, ..., T_{CW_n}$）；
未知量：相机与机械臂基座的变换 $T_{BC}$（即X，需标定求解）。

2.2.2 变换回路构建

当机械臂带动标定板运动两次，到达两个不同位姿 $E_1$（标定板 $W_1$）和 $E_2$（标定板 $W_2$）时，构建闭合变换回路：

第一次运动（位姿1）：机械臂基座 → 相机 $C$ → 标定板 $W_1$ → 机械臂末端 $E_1$ → 机械臂基座
变换关系：$T_{BE_1} = T_{BC} \times T_{CW_1} \times T_{W_1E_1}$
第二次运动（位姿2）：机械臂基座 → 相机 $C$ → 标定板 $W_2$ → 机械臂末端 $E_2$ → 机械臂基座
变换关系：$T_{BE_2} = T_{BC} \times T_{CW_2} \times T_{W_2E_2}$
由于标定板与机械臂末端刚性连接，$T_{W_1E_1} = T_{W_2E_2} = Y$（固定变换，无需求解）；相机与机械臂基座相对静止，$T_{BC} = X$（未知变换矩阵）。因此：
$$ T_{BE_1} = X \times T_{CW_1} \times Y $$
$$ T_{BE_2} = X \times T_{CW_2} \times Y $$

2.2.3 方程简化（AX=XB形式）

定义两个关键变换：

$A = T_{BE_1}^{-1} \times T_{BE_2}$：机械臂末端从位姿1到位姿2的相对变换（已知）；
$B = T_{CW_1}^{-1} \times T_{CW_2}$：标定板（相对于相机）从位姿1到位姿2的相对变换（已知）。
将两个回路方程变形为 $Y = T_{CW_1}^{-1} \times X^{-1} \times T_{BE_1}$ 和 $Y = T_{CW_2}^{-1} \times X^{-1} \times T_{BE_2}$，联立后整理得到：
$$ T_{CW_1}^{-1} \times X^{-1} \times T_{BE_1} = T_{CW_2}^{-1} \times X^{-1} \times T_{BE_2} $$
两边左乘 $T_{CW_1}$、右乘 $T_{BE_2}^{-1} \times X$，最终化简为：
$$ A X = X B $$
惊喜的是，Eye-to-Hand系统的核心方程与Eye-in-Hand完全一致！二者的区别仅在于A和B的物理含义不同，但数学求解方法完全通用——这体现了手眼标定的数学统一性。

三、数学推演：AX=XB方程的求解

3.1 方程本质分析

AX=XB是一个关于4×4齐次变换矩阵X的非线性方程组，其中A和B是已知的4×4齐次变换矩阵（由机械臂运动和相机标定结果得到）。将X拆分为旋转矩阵R（3×3）和平移向量t（3×1），则方程可分解为旋转部分和平移部分的求解：

3.1.1 旋转部分求解（R）

齐次变换矩阵的旋转部分满足：$A_R R = R B_R$，其中 $A_R$ 和 $B_R$ 分别是A和B的3×3旋转矩阵。这是一个矩阵方程，可通过正交 Procrustes 问题或Tsai-Lenz算法求解。
以正交Procrustes方法为例，其核心思想是将方程转化为最小二乘问题：
$$ \min_R | A_R R - R B_R |_F^2 $$
其中 $| \cdot |F$ 是Frobenius范数。通过矩阵向量化和奇异值分解（SVD），可解得：
$$ R = U V^T $$
其中U和V是矩阵 $M = \sum^n (B_Rⁱ⁾T A_R^i$ 的奇异值分解结果（$M = U \Sigma V^T$），n为机械臂运动的次数（通常采集10~20组数据以提高精度）。

3.1.2 平移部分求解（t）

当旋转矩阵R求解完成后，平移部分满足线性方程：
$$ A_R t - t = -A_t + R B_t $$
其中 $A_t$ 和 $B_t$ 分别是A和B的3×1平移向量。将方程整理为：
$$ (A_R - I) t = R B_t - A_t $$
这是一个线性方程组 $C t = d$（其中 $C = A_R - I$，$d = R B_t - A_t$），可通过最小二乘法求解：
$$ t = (C^T C)^{-1} C^T d $$

3.1.3 完整解X的构成

将求解得到的旋转矩阵R和平移向量t代入齐次变换矩阵形式，即可得到完整的变换矩阵X：
$$ X = \begin{bmatrix} R & t \ 0^T & 1 \end{bmatrix} $$

3.2 常用求解算法对比

AX=XB方程的求解算法有多种，不同算法在精度、效率和鲁棒性上各有优劣，适用于不同场景：

算法名称	核心特点	精度	效率	适用场景
Tsai-Lenz算法	分离旋转和平移求解，经典算法	中高	高	工业场景实时标定、算力有限的嵌入式平台
迭代法（如Newton-Raphson）	基于非线性优化，迭代收敛	高	中	高精度需求场景（如精密装配）
解析法（Procrustes+最小二乘）	闭式解，无迭代，稳定性强	中	高	快速标定、多组数据融合
基于李代数的方法	将旋转和平移转化为向量空间求解，数学严谨	高	中	学术研究、复杂场景标定
在实际应用中，Tsai-Lenz算法因兼顾精度和效率，是工业界应用最广泛的方法；若需更高精度，可采用迭代法或融合多组数据的解析法。

3.3 多组数据融合（提高标定精度）

仅通过两次机械臂运动（一组A和B）求解X，精度往往较低。实际标定中通常采集10_{20组数据（机械臂运动10}20个不同位姿，每次拍摄标定板图像并记录机械臂位姿），通过以下方式融合：

对每组数据（$A_i, B_i$），构建方程 $A_i X = X B_i$；
将所有方程转化为统一的线性方程组 $M x = 0$（其中x是X的向量化形式）；
通过最小二乘法求解超定方程组，得到最优解X。
多组数据融合可有效抑制测量噪声（如机械臂运动误差、相机标定误差），显著提高标定精度——这是实际操作中不可或缺的步骤。

四、实际应用与操作指南

4.1 典型应用场景

手眼标定的核心价值是实现“视觉引导机械臂”，其典型应用场景包括：

4.1.1 工业自动化抓取

场景：传送带上随机摆放的零件抓取、无序堆叠物料的分拣；
流程：相机拍摄目标→识别目标在相机坐标系下的坐标→通过手眼标定变换矩阵X转换为机械臂基座坐标系坐标→机械臂运动至目标位置完成抓取；
要求：标定精度需达到±0.1~±1mm（根据零件尺寸调整）。

4.1.2 精密装配与测量

场景：电子元器件焊接、微小零件装配、产品尺寸在线检测；
流程：相机拍摄装配目标或被测物体→通过标定转换为机械臂坐标→机械臂执行精密定位或测量动作；
要求：标定精度需达到±0.01~±0.1mm，需结合高精度标定板和相机。

4.1.3 视觉伺服控制

场景：机械臂跟踪动态目标、柔性环境下的自适应操作；
原理：通过相机实时反馈目标位置偏差，结合手眼标定关系，动态调整机械臂运动指令；
要求：标定鲁棒性强，需抵抗动态环境中的噪声干扰。

4.1.4 医疗机器人与科研场景

场景：手术机器人精准操作、机器人辅助实验平台；
特点：对标定精度和安全性要求极高，需结合无菌标定板和高精度传感器。

4.2 实际操作步骤（以Eye-in-Hand为例简单讲解，详细过程会发在后续的博客）

4.2.1 前期准备

硬件选型：
- 相机：工业相机（推荐分辨率≥1280×960，帧率≥30fps），若需三维定位可选用深度相机（如Kinect、Realsense）；
- 标定板：棋盘格标定板（格子尺寸建议5~20mm，根据工作空间大小选择，需保证平整度）；
- 机械臂：带API接口的工业机械臂或协作机械臂（支持读取末端位姿，重复定位精度≤±0.1mm）。
软件工具：
- 相机标定：OpenCV（张正友标定法）、Matlab Camera Calibrator Toolbox；
- 手眼标定：OpenCV（自定义求解AX=XB）、Robotics Toolbox（Matlab/Python）、ROS（Robot Operating System）内置手眼标定包。

4.2.2 具体操作流程

相机内参标定：
- 拍摄10~20张不同角度、不同距离的标定板图像；
- 使用OpenCV或Matlab工具求解相机内参矩阵和畸变系数，保存结果用于后续外参计算。
机械臂与相机安装：
- 将相机固定于机械臂末端（确保刚性连接，无松动）；
- 将标定板固定于工作台（与机械臂基座相对静止，确保无位移）。
数据采集：
- 控制机械臂运动至不同位姿（建议10~20个），每次运动后确保相机能清晰拍摄到标定板（标定板需占据图像中心区域，无严重畸变）；
- 记录每个位姿下的机械臂末端位姿 $T_{BE_i}$（通过机械臂API读取）；
- 拍摄每个位姿下的标定板图像，使用相机内参求解外参 $T_{CW_i}$（旋转矩阵+平移向量）。
求解手眼变换矩阵X：
- 对每组相邻位姿数据，计算机械臂相对变换 $A_i = T_{BE_{i-1}}^{-1} \times T_{BE_i}$ 和相机相对变换 $B_i = T_{CW_{i-1}} \times T_{CW_i}^{-1}$；
- 采用Tsai-Lenz算法或多组数据融合法求解AX=XB，得到X（相机与机械臂末端的变换矩阵）。
标定精度验证：
- 选取一个未参与标定的机械臂位姿，拍摄标定板图像，得到目标在相机坐标系下的坐标 $P_C$；
- 通过X将 $P_C$ 转换为机械臂末端坐标系坐标 $P_E = X \times P_C$；
- 机械臂运动至 $P_E$ 对应的基座坐标系位置，观察末端执行器与标定板目标点的重合度——误差在允许范围内（如±0.1mm）则标定有效。

4.3 关键注意事项

硬件安装：相机与机械臂末端、标定板与工作台的连接必须刚性，避免运动过程中产生松动或形变（这是标定误差的主要来源之一）。
数据采集：
- 机械臂运动范围需覆盖工作空间，位姿分布均匀（避免集中在某一区域）；
- 拍摄的标定板图像需清晰，无模糊、反光，标定板角点需完整识别；
- 数据组数建议不少于15组，组数越多，噪声抑制效果越好。
误差控制：
- 先校准机械臂自身的重复定位精度（若机械臂误差过大，需先进行机械校准）；
- 相机标定需考虑畸变校正（尤其是广角相机，畸变对精度影响显著）；
- 标定环境需稳定（避免光照剧烈变化、振动等）。
重新标定时机：
- 相机或机械臂末端的安装位置发生变动时；
- 机械臂进行维护、关节参数调整后；
- 标定精度验证不通过时（误差超过允许范围）。

五、总结与展望

手眼标定是连接机器人视觉与运动控制的核心技术，其本质是通过坐标系变换回路建立AX=XB方程，求解相机与机械臂的刚性变换关系。无论是Eye-in-Hand还是Eye-to-Hand架构，都遵循“已知运动+视觉测量→构建方程→求解变换”的核心逻辑，仅在系统结构和参数定义上存在差异。
在实际应用中，标定精度直接决定了机械臂与环境交互的可靠性——工业场景中需兼顾精度与效率，科研场景中需追求极致精度，而合理的硬件选型、规范的操作流程和多组数据融合是实现高精度标定的关键。
未来，随着深度学习技术的发展，手眼标定正朝着“无标定”“自标定”方向演进：通过深度神经网络直接学习相机与机械臂的坐标映射关系，无需依赖传统标定板和复杂的数学求解，有望简化操作流程、提高鲁棒性。但在高精度场景中，传统手眼标定因其数学严谨性和稳定性，仍将长期占据主导地位。
希望本文能为从事机器人视觉相关工作的读者提供清晰的原理指引和实用的操作参考——手眼标定的核心是理解“坐标系变换”，掌握这一核心逻辑后，无论面对何种场景，都能灵活调整方案，实现精准的视觉引导控制。

posted @ 2025-12-18 00:35 TTGF 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

ChenAI-TGF