The 16th Zhejiang Provincial Collegiate Programming Contest

传送门：

Problem A

Problem B

题意：

有一个数组 $a_1 、 a_2 \dots a_n$ ，其中 $x = \sum_{k=1}^nka_k$ ， $y = \sum_{k=1}^nka_k^2$ ，现在数组 $a$ 中有两个数字被交换了，现在给你交换后的数组 $b_1 、b_2 \dots b_n$ 现在问你有多少种交换方案，使得数组 $a$ 变成 $b$ 。

分析：

细节题，写起来还是蛮糟心的……

若将位置 $i$ 和位置 $j$ 交换，设交换前的 $x$ 的值为 $X$ ,交换后的值是 $X'$ 有： $X'=X-i*a_i+j*a_i-j*a_j+i*a_j$ $X'-X=(j-i)*(a_i-a_j)$

同理对 $y$ 值也有： $Y'=Y-i*a_i^2+j*a_i^2-j*a_j^2+i*a_j^2$ $Y'-Y=(j-i)*(a_i^2-a_j^2)$

将上述两式相除可得：

$\frac{Y'-Y}{X'-X}=a_i+a_j \dots 1$

而又有 $X'-X=(j-i)*(a_i-a_j) \dots 2$

而 $Y'-Y和X'-X$ 我们都是已知的，因此我们可以枚举 $a_i$ ，并用 $1$ 式去求解出 $a_j$ ，最后用求解出来的 $a_j$ 代入到 $2$ 式进行验证是否合理。最后注意边界细节。

这题的代码细节还是相对来说比较繁琐的，需要理清思路才行……

代码：

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
typedef long long ll;
int a[maxn];
unordered_map<ll,int>mp;
int main()
{
    //freopen("in.txt","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--){
        int n;
        ll x,y,X=0,Y=0;
        scanf("%d%lld%lld",&n,&x,&y);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            X+=1ll*a[i]*i;
            Y+=1ll*a[i]*a[i]*i;
        }
        ll tmpx=x-X;
        ll tmpy=y-Y;
        ll res=0;
        if(tmpx==0&&tmpy==0){
            mp.clear();
            for(int i=1;i<=n;i++) mp[a[i]]++;
            for(int i=1;i<=n;i++){
                if(mp[a[i]]){
                    ll t=mp[a[i]];
                    res+=t*(t-1)/2;
                    mp[a[i]]=0;
                }
            }
            printf("%lld\n",res);
        }
        else{
            if(tmpx==0||tmpy%tmpx!=0){
                puts("0");
                continue;
            }
            ll tmp=tmpy/tmpx;
            for(int i=1;i<=n;i++){
                ll aj=tmp-a[i];
                if(aj<=0||aj>100000) continue;
                ll aa=a[i]-aj;
                if(aa==0) {
                    continue;
                }
                if(tmpx%aa!=0) continue;
                int jj=tmpx/aa+i;
                if(jj<=0||jj>n||jj<i) continue;
                //cout<<aj<< ' '<<aa<<" "<<jj<<endl;
                if(a[jj]==aj)res++;
            }
            printf("%lld\n",res);
        }
    }
    return 0;
}

Problem C

Problem D

题意：

你现在有 $n$ 个点，对于第 $i$ 个点，可以到达第 $i-1$ 、 $2*i$ 、 $2*(i+1)$ 、 $\left \lfloor \frac{i}{2} \right \rfloor$ 号点。现在问你从 $1$ 号点开始的哈密顿路径。

分析：

一道非常有意思的题目。

我们需要发掘题目中隐藏的信息。

首先，假设该顶点不能到达第 $i-1$ 个结点，对于任意一个点 $i$ ，因为它能够到达第 $2*i$ 、 $2*(i+1)$ 以及 $\left \lfloor \frac{i}{2} \right \rfloor$ ，因此，由这些点所形成的结点必然能够形成一棵完全二叉树

显然一颗树是不能形成哈密顿回路的，显然这题的重中之重就是如何怎么选择去到第 $i-1$ 个结点。

现在，如果加上到第 $i-1$ 号结点的边，那么这张图将会变成这样：
在这里插入图片描述
而对于某一个结点 $i$ ，如果我们一直遍历 $2*i$ 或 $2*(i+1)$ 号结点，那么答案显然不会变优，因此我们需要在遍历图的过程中优先选择往 $i-1$ 号结点访问，倘若 $i-1$ 号结点被访问过了，则再访问第 $2*i$ 号点。

这样进行dfs遍历之后，我们会发现我们形成了这样一棵dfs树：

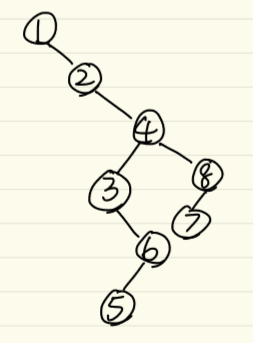
在这里插入图片描述
这棵dfs树所表示的即为遍历所有结点的顺序。此时我们只需要对这棵dfs树先遍历右儿子再遍历左儿子并把整张图输出即可。

需要注意的是，我们需要在遍历每一个点的时候判断一下当前点的第 $2*(i+1)$ 号结点是否曾经在第一次dfs中访问，如果没有，则需要在此时输出。

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
typedef pair<int,int>pll;
pll q[maxn];
bool vis[maxn];
int n;
bool check(int x){
    return x>=1&&x<=n&&!vis[x];
}
void dfs(int x){
    vis[x]=true;
    if(check(x-1)){
        q[x].first=x-1;
        dfs(x-1);
    }
    if(check(x<<1)){
        q[x].second=x<<1;
        dfs(x<<1);
    }
}
void dfs2(int x){
    if(x==1) printf("1");
    else printf(" %d",x);
    if(check(x<<1|1)){
        vis[x<<1|1]=1;
        printf(" %d",x<<1|1);
    }
    if(q[x].second!=0){
        dfs2(q[x].second);
    }
    if(q[x].first!=0) dfs2(q[x].first);
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        for(int i=1;i<=n;i++) vis[i]=false,q[i].first=q[i].second=0;
        dfs(1);
        dfs2(1);
        puts("");
    }
    return 0;
}

Problem E

题意：

给你一个长度为长度为 $n$ 的序列，每次你可以选取其中的某一个数 $a_i$ ，你可以把 $a_i$ 放到序列的首位。问最少进行多少次操作可以使得序列单调递增。

分析：

先记录原序列中每个数的位置 $id_1$ ，再记录升序排序之后的位置 $id_2$ ，最后再根据 $id_1$ 升序排序记录，从大到小遍历序列，如果 $id_1=id_2$ 则将答案 $-1$ 即可。

注意如果存在两个值相同时，需要特判。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
struct S{
    int x,id,idd;
}a[maxn];
bool cmp(S a,S b){
    if (a.x==b.x) return a.id<b.id;
    return a.x<b.x;
}
bool cmp1(S a,S b){
    return a.id<b.id;
}
int b[maxn];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin>>t;
    while (t--){
        int n;
        cin>>n;
        for (int i=1;i<=n;i++) {
            cin>>a[i].x;
            a[i].id=i;
            b[i]=0;
        }
        sort(a+1,a+n+1,cmp);
        int pre=a[1].x,cnt=1;
        a[1].idd=1;b[1]=1;
        for (int i=2;i<=n;i++) {
            if (pre!=a[i].x) {
                pre=a[i].x;
                a[i].idd=++cnt;
                b[cnt]++;
            } else a[i].idd=cnt,b[cnt]++;
        }
        sort(a+1,a+n+1,cmp1);
        int id=cnt,ans=n;
        for (int i=n;i>=1;i--){
            if (a[i].idd==id) {
                ans--;
                b[id]--;
                if (b[id]==0) id--;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

Problem F

温暖的签到题，随便模拟一下就好了

Problem G

温暖的签到题，暴力枚举一下就好了

Problem H

枚举删除每一位，记录一下最小值即可。

#include <bits/stdc++.h>
#define maxn 100005
using namespace std;
int a[maxn];
int ans[maxn];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            ans[i]=0;
        }
        int sum=0;
        for(int i=2;i<n;i++){
            if(a[i]>a[i-1]&&a[i]>a[i+1]){
                ans[i]++;
                sum++;
            }
        }
        int mn=0;
        for(int i=2;i<n;i++){
            int tmp=0;
            if(i<n-1){
                if(!(a[i+1]>a[i-1]&&a[i+1]>a[i+2])&&ans[i+1]){
                    tmp--;
                }else if(a[i+1]>a[i-1]&&a[i+1]>a[i+2]&&!a[i+1]) tmp++;
            }
            if(i>2){
                if(!(a[i-1]>a[i+1]&&a[i-1]>a[i-2])&&ans[i-1]){
                    tmp--;
                }else if(a[i-1]>a[i+1]&&a[i-1]>a[i-2]&&!ans[i-1]) tmp++;
            }
            if(a[i]>a[i-1]&&a[i]>a[i+1]&&ans[i]) tmp--;
            mn=min(mn,tmp);
        }
        printf("%d\n",sum+mn);
    }
    return 0;
}

Problem I

发现斐波那契数列的奇偶性存在着大小为 $3$ 的循环节，故直接找规律求解即可。

#include <bits/stdc++.h>
using namespace std;
const int maxn=100007;
char a[maxn],b[maxn];
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    int t;
    cin>>t;
    while (t--){
        cin>>a>>b;
        int n=strlen(a),m=strlen(b);
        int x=0,y=0;
        for (int i=0;i<n;i++){
            x+=a[i]-'0';
            x%=3;
        }
        for (int i=0;i<m;i++) {
            y+=b[i]-'0';
            y%=3;
        }
        int ans;
        if (x==1){
            if (y==0) ans=0;
            else if (y==1) ans=1;
            else ans=0;
        }else if (x==2){
            if (y==1) ans=0;
            else ans=1;

         }else {
            if (y==1) ans=1;
            else ans=0;
         }
         cout<<ans<<endl;
    }
    return 0;
}

Problem J

题意：

有 $n$ 个人和 $m$ 种关系，每个人以此进场，如果某个人发现场上没有自己的朋友，则就会产生一点不高兴值。现在让你设计一个字典序最小的进场顺序，使得产生的不高兴值最少。

分析：

考虑使用并查集维护这若干个人的关系。因为最后需要我们设计一个字典序最小的顺序，故在我们并查集合并的时候，我们考虑优先把编号大的人合并到编号小的人上。

最后，倘若需要产生的不开心的值最大，显然我们需要优先让并查集集合大小大且父亲编号最小的人优先进场。因此我们只需要根据编号从小到达遍历每一个人，将每一个这样的集合中的父亲结点压入队列中，最后进行bfs扩展输出结果即可。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+7;
priority_queue<int,vector<int>,greater<int> >q;
vector<int>a[maxn];
int f[maxn];
bool vis[maxn];
int find(int x){
    return x==f[x]?x:f[x]=find(f[x]);
}
void join(int x,int y){
    int xx=find(x),yy=find(y);
    if (xx==yy) return;
    if (xx<yy) f[yy]=xx;
    else f[xx]=yy;
}
int main(){
   // freopen("in.txt","r",stdin);
    int t;
    scanf("%d",&t);
    while (t--){
        int n,m,x,y;
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++) {
            f[i]=i,vis[i]=0;
            a[i].clear();
        }
        for (int i=1;i<=m;i++){
            scanf("%d%d",&x,&y);
            a[x].push_back(y);
            a[y].push_back(x);
            join(x,y);
        }
        int ans=0;
        while (!q.empty()) q.pop();
        for (int i=1;i<=n;i++){
            x=find(i);
            if (!vis[x]) {
                q.push(x);
                vis[x]=1;
                ans++;
            }
        }
        printf("%d\n",ans);
        x=q.top();q.pop();
        printf("%d",x);
        for (int i=0;i<a[x].size();i++) {
            y=a[x][i];
            if (!vis[y]) {
                vis[y]=1;
                q.push(y);
            }
        }
        while (!q.empty()){
            x=q.top();
            q.pop();
            printf(" %d",x);
            for (int i=0;i<a[x].size();i++){
                 y=a[x][i];
                if (!vis[y]) {
                    vis[y]=1;
                    q.push(y);
                }
            }
        }
        printf("\n");
    }
    return 0;
}

Problem K

题意：

给你两个串 $str_1~~str_2$ ，现在让你再 $str_1$ 中选取一段区间 $[l,r]$ ，将这段区间反转，如果经过反转后的串 $str_1'=str_2$ 则说区间 $[l,r]$ 是可行的。现在问你有多少段可行的区间。

分析：

分两类情况进行讨论：

如果两个串完全一样，则显然我们要求的就是这两个串中的本质不同的回文字串的个数。
如果两个串不完全相同，我们需要先找到左边第一个不相同的位置 $l$ ，以及右边第一个不相同的位置，如果在区间 $[l,r]$ 中，两个串满足 $str_1$ 的头等于 $str_2$ 的尾，则我们把区间 $[l,r]$ 的字符简化为一个标记字符 $?$ ，则此时就形成了一个新的串 $str_1''$ 。此时我们只需要求出以 $?$ 为中心最长的回文串即可。

而上述的求解回文串的个数的操作，我们可以用Manache或者回文树去解决。

代码：

#include <bits/stdc++.h>
#define maxn 2000005
using namespace std;
typedef long long ll;
char str1[maxn],str2[maxn];
char Ma[maxn*2];
int Mp[maxn*2];
void Manacher(char *s,int len){
    int l=0;
    Ma[l++]='$';
    Ma[l++]='#';
    for(int i=0;i<len;i++){
        Ma[l++]=s[i];
        Ma[l++]='#';
    }
    Ma[l]=0;
    int mx=0,id=0;
    for(int i=0;i<l;i++){
        Mp[i]=mx>i?min(Mp[2*id-i],mx-i):1;
        while(Ma[i+Mp[i]]==Ma[i-Mp[i]]) Mp[i]++;
        if(i+Mp[i]>mx){
            mx=i+Mp[i];
            id=i;
        }
    }
}
void Do(char *str){
    Manacher(str,strlen(str));
    ll res=0;
    int L=strlen(Ma);
    for(int i=2;i<L;i++){
        res+=Mp[i]/2;
    }
    printf("%lld\n",res);
}
int main()
{
    int t;
    //freopen("in.txt","r",stdin);
    scanf("%d",&t);
    while(t--){
        scanf("%s",str1);
        scanf("%s",str2);
        int l=0,r=strlen(str1)-1;
        int len=strlen(str1);
        while(l<len&&str1[l]==str2[l]) l++;
        while(r>=0&&str1[r]==str2[r]) r--;
        if(l>=r){
            Do(str1);
            continue;
        }
        ll res=0;
        int ll=l,rr=r;
        while(l<=rr&&r>=ll&&str1[l]==str2[r]&&str1[r]==str2[l]) l++,r--;
        if(l<=r){
            puts("0");
        }
        else{
            char tmp[maxn];
            int cnt=0;
            for(int i=0;i<ll;i++){
                tmp[cnt++]=str1[i];
            }
            tmp[cnt++]='?';
            for(int i=rr+1;i<len;i++){
                tmp[cnt++]=str1[i];
            }
            tmp[cnt]='\0';
            Manacher(tmp,strlen(tmp));
            //tmp[cnt]='\0';
            int L=strlen(Ma);
            for(int i=0;i<L;i++){
                if(Ma[i]=='?'){
                    res+=Mp[i]/2;
                    break;
                }
            }
            printf("%lld\n",res);
        }
    }
return 0;
}

Problem L

Problem M

posted @ 2019-04-28 11:26 ChenJr 阅读(196) 评论(0) 收藏举报

刷新页面返回顶部

ChenJr