2025 年南京大学计算机学科体验专题营 游记

【洛谷专栏】。

前言

第一次夏令营，也许是，最后一次。

今天开始写，以前的事情视重要程度补充在里面。

正文

7.2?

在广东集训时看见了 Luogu Academic 群里有南京大学的同学转发夏令营的报名通知。

各类优秀的2026、2027届高中毕业学生，尤其是符合以下条件之一的：

• 获得信息学省级赛区（NOIP提高组），或NOI春季赛一等奖（针对部分NOIP未举办省份）；
• 获得数学省级赛区（全国高中数学联赛）一等奖；
• 获得物理省级赛区（全国中学生物理竞赛）一等奖；
• 在以上两个不同比赛中均获得二等奖。

看下来只有年级是符合的哈哈哈。

没有一等奖，也没有两个学科的二等奖，所以把这事情放一边了没再理会。

8.6

上午乘坐飞机从广州白云国际机场，于下午到达南京禄口国际机场。

到达酒店时已经下午四点了，所以下午取消了原有的行程安排。

稍作休息后和时隔六年未见的小学同学共进晚餐，互相交流了一下当地的高考形式和政策。

众所周知的，江苏省统一采用新高考 I 卷，肯定是比重庆的新高考 II 卷难的，不过近几年也有在传重庆改用新高考 I 卷，总之压力上到我们这几届了哈，看谁先中奖。

不过话说回来，我难人难，我易人易，无论试卷难度如何改变，相对稳定不变的是大学在省份的录取位次。

学校	招生省份	录取批次	专业组/类别要求	2024最低分	2024最低位次
南京大学	重庆	本科批	物理类	677	447
南京大学	江苏	本科批（普通类）	07组（物+不限）	661	2296
南京大学	江苏	本科批（普通类）	09组（物+化）	663	1987
南京大学	江苏	本科批（普通类）	08组（物+化）	667	1405
南京大学	江苏	本科批（中外合作）	11组（物+化）	647	5643
东南大学	重庆	本科批	物理类	655	1941
东南大学	江苏	本科批（普通类）	06组（物+化）	660	2297
东南大学	江苏	本科批（普通类）	07组（物+不限）	656	3027
东南大学	江苏	本科批（普通类）	08组（物+化）	646	5644

以上是 Deepseek 整理的 2024 年公布的南京大学和东南大学在两省（市）物理类的录取情况。

可以发现在江苏省考这两所高校的难度是不相上下的，但在重庆市就是天差地别。

我爸也是第一次听说，毕竟他也没有研究过其他省份，所以和我同样惊讶。

革命尚未成功，同志仍须努力。

8.7

旅程细节就不在这里过多讲述了，想了解的可以去看我的 QQ 空间，这里挑一些重点讲。

下午参观南京大学（鼓楼校区），从南苑骑到北苑。

在某个时刻听我爸说我的报名审核通过了，第一反应还是有些激动，二等奖也能破格，第二反应是清华冬令营都要我说明我还是有点水平（不是。

在校园里四处骑车，参观了校史馆，里面有很多耳熟能详的科学家个人介绍，说明南京大学还是有深厚的底蕴。

逛南京大学文创店，一眼就被桌面立牌萌化了，一只小猫在船上“划水中”真的好可爱。

但是贫穷限制了我的想象力，所以除了上面这个还买了个南京大学文件袋就离开了。

8.11

看不懂但是大受震撼。

但是感觉确实挺真的。

8.13

自己花心思出了很久的题被高水平选手喷“根本不是题”。

还是有点伤自尊的，难过了很久。

8.14

达成成就课题模式金 48。

选曲仅供参考 Retribution IN16.2 98.2w，祈神 IN16.4 98.4w，时停 IN16.0 98.4w。

8.15

晚上挑战 @Whiking 进行别样的乒乓球大战，取得了 4:1 大胜！

8.16

在音游圈吃瓜，看到了如下名言：

我打音游好学校好你们就认为我是个好人了吗？

8.17

如此，年老。

8.18

考试，NOI plus！！！我不好说什么，反正没有三位数 /hanx。

惊奇发现两年前写的文章 化学方程式 突破了 100 赞，决定进行大更新。

成为了所谓的网红以后就是不一样，把这个古早作品翻出来又引起了一波流量。

8.19

因为 tad_ao 出差了，所以高 2028 届的同学被迫移动到了初 2026 届同学的机房，他们表示“没有一点人与人之间的信任”。

我觉得他们也对不起老师的信任吧。

他们吐槽机房木凳很硬没有靠背，我叫他们去尝试和老师协商换座椅，作为一个有基本人情的老师肯定都会同意的。

先做了一个神奇测试，测抑郁程度的，莫名其妙被诊断为轻度抑郁，我自己都不信。

接着完成了另一个神奇小测试你还会单身多久，结果是……

一年后的我，已经高三了，看来还是要专注于学习呢。

但愿好饭不怕晚。

拿到了 @cyh20100812 的化学作业，在少量她已经完成题目中惊奇的发现了 \(\mathrm{Al + 4OH^-} \xlongequal{\quad} \mathrm{[Al(OH)_4]^-}\)。

元素是守恒的，电子是凭空消失的。

写了一天的化学作业，非常好作业让我死去的必修一知识突然开始旋转，在下午完工了。

2025 年暑假 高 2028 届化学作业参考答案，密码可以直接私信我获取，50 只是开玩笑……

晚自习被教练拉到隔壁去谈话，才发现我是我们学校代表队水平最低的人。

还没开始考就给自己上压力了吗。

回到家以后和一个才退役的学妹略微交流，我想我的行动已经足够证明自己了，但是又有什么作用呢。

现实既如此，也不必遗憾。

8.20

上午考试，分数还能看，排名一般般。

后桌 @XiaoShanYunPan 一直在发布一些低质言论显得自己非常强大，结果他说前三题都是入门级题目结果都挂了，笑死。

没有同桌就开始讨厌后桌了（流汗。

Lyrith -迷宮リリス- AT16.5 打出了 99.34% 的不错成绩，上位 b8，最难 4k 轻松全 P，轮指打 5 纵连轻松爆炸。

会打 16.5/16.7 的 4k/5k，但还是研究不明白 16.6 的那一堆牛鬼蛇神。

8.21

这周一晚上在南京的小学同学告诉我他来重庆了。

但是他 23 日回南京，只能说是很遗憾地完美错过了哈，都没有在重庆好好招待他。

《 双 氢 飞 起 来 》

网络流，从来没学懂，这次还是一样。

考场上肯定是，不会建模，就算是建模了也不会写求解网络流算法。

学习了网络流的进阶：有/无源汇上下界网络流，这东西还是太困难了。

写模板题写了一天，直接被潘总质问了（哭。

谴责教练 @tad1 不把多的雪糕送我一个，好坏的人（流泪。

中午录制了 400 粉福，下载链接，不建议打开声音，因为打开声音带来的任何后果本人概不负责。

8.22

前往重庆江北国际机场 T2 航站楼，自从 T3 修好后几乎没再去。

相比 T3 确实显得有点黯然失色了。

飞机由于航路调整延误了两个小时，所以喜提飞机餐，有点饿了餐食和饮料都要了双份的（不要脸。

下午就直接乘坐地铁去南京大学报道了。

北门进去直接就是软件学院，乘坐电梯上到 5 楼，签字后领到了营员证和刻了本次活动名字的咖啡杯！意外之喜了。

顺便试机，在试机赛中拿到了 200 分 12 名的好成绩，第三题是用来提交视频文件的 md5 码的。

酒店的卫生间和卧室中间的玻璃是透明的，这怎么洗。

回来问前台才知道厕所里有个雾化开关，长见识了。

随便复习了一点组合数学就睡觉了。

8.23

开营仪式，短暂的讲话，宣布开营后笔试开始。

1. 群论题，题目描述记不得了，\(G\) 是一个 \(pq\) 阶群，有质数 \(p,q(p < q)\)，满足 \(p \mid q-1\)，证明 \(G\) 是循环群。（给了一个 S 开头定理的材料）

2. 两个偏序结构 \((A,\le_A),(B,\le_B)\)，如果存在映射 \(f:A\rightarrow B\)，对于所有 \(a_1,a_2 \in A\)，使得 \(a_1 \le_A a_2 \Leftrightarrow f(a_1) \le_B f(a_2)\)，则称他们“序相似”。

   求证：\(A\) 是一个可数集合，\(\preccurlyeq\) 是 \(A\) 的偏序关系，存在集合 \(B \subseteq \mathbb{Q} \cap (0,1)\)，使得 \((A,\preccurlyeq),(B \le)\) 序相似。

3. 有一个正整数集合 \(S\)，求是否存在一个子集 \(T\) 满足元素和为 \(2025\)。

   （这是一段 NP-Hard 问题，NP 问题，多项式时间规约的材料）

   请问这个问题是否是 NP-Hard 问题，若是请给出证明，若不是请给出一个多项式时间内解决问题的算法。

4. \(2025\)-bit 的寄存器，至少有一个 \(0\)，至少有一个 \(1\)，不知道具体位置上的值。

   操作 \(A(u,v)\) 为 \(a_u = a_u \operatorname{xor} a_v\)，其中 \(u \neq v\)。

   经过一系列连续的操作后，可以明确的知道哪些位置（操作后）是 \(0\) 或 \(1\)，最多可以知道几个位置？

5. \(m\) 条边的简单无向图 \(G(V,E)\)，证明：一定存在两个集合 \(U,W\)，满足 \(U \cap W = \varnothing, U \cup W = V\)，\(U\) 和 \(W\) 的导出子图边数都小于 \(\frac m 3\)。

上面是回忆的题目，可能描述不太准确。

总之就是除了第三题一道题都不会做。

中午就在学校北门对面的第一泉酒家吃饭，还可以，旁边桌是广附的同学？

下午是机试。

排座位

\(n\) 个座位排成一排，有 \(n\) 个人按照以下规则依次落座：

• 第一个人可以选择任意一个座位落座。
• 后来的人选择离有人座位的最远的空座位落座，如果距离相同可以选择任意一个。

例如 \((2,4,1,3),(2,4,3,1)\) 是合法的落座序列，但是 \((2,1,3,4),(2,3,1,4)\) 不是。

落座序列不同即存在一个人的选择座位不同。

求有多少组不同的落座序列，答案对 \(m\) 取模。

\(1 \le n \le 10^5, 1 \le m \le 10^9\)。

黑暗中的舞者

有 \(n\) 个人，第 \(i\) 个人的坐标是 \((x_i,y_i)\)。

你作为舞者要去叫醒这 \(n\) 个人，在每个时刻你可以唤醒和你 \(x\) 坐标相同或者 \(y\) 坐标相同的人。

起点和中点可以自由选择，每个时刻你可以选择向四连通的相邻位置移动，形式化地，\((x_1,y_1),(x_2,y_2)\) 相邻当且仅当 \(\vert x_1 - x_2 \vert + \vert y_1 - y_2 \vert = 1\)。

求叫醒所有人需要多长时间（不包含起点时间）。

例如现在有 \(3\) 个人的坐标分别在 \((1,1),(2,2),(3,3)\)，你从 \((1,2)\) 出发可以叫醒第一个人和第二个人，移动到 \((1,3)\) 可以叫醒第三个人，总时间为 \(1\)。

\(1 \le n \le 5\times 10^5, 1 \le x,y \le 10^9\)。

六边形

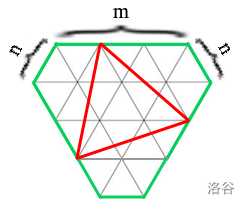
这是一个 \((m,n)\)-六边形，内部由等边三角形组成的格点图。

你需要数出在其中端点在格点上，边不与内部的等边三角形重合（不是相交）的非退化等边三角形。

例如图中红色的三角形就是其中之一。

\(1 \le n,m \le 10^{10}\)。

上来简单观察了一下 A 合法序列，没有思路。

发现有人通过了 B，于是去看 B。

策略显然是走 \(x\) 的连续段和 \(y\) 的连续段。

所以对 \(x\) 进行排序，枚举按 \(x\) 走的右端点，维护 \(\max_{j=1}^i y_i - \min_{j=1}^i y_i - x_{i+1}\) 的最小值即可。

大概半个小时把 B 写完了并通过了全部大样例，回去看 A。

第一个放置的位置在序列上对称方案数量相同，正确性显然。

对于所有空段一定是按中点分开，奇数段分成相同的两段，偶数段分为长度不同的两段。

对于一个长度为 \(u\) 的偶数段，可以和奇数段 \(u-1\) 一起处理，因为可以在这两个段可以按任意顺序选择，所以有一个阶乘的贡献。特别地，偶数段中有两种选择，所以有 \(2\) 次幂的贡献。

\(u=2\) 需要特殊处理，不再有 \(2\) 的贡献。

一个第一次选择的位置答案全部相乘，对于每一个第一次选择位置的答案求和。

回来看 B 觉得这么难的数据结构题一遍写过不太对，所以拍了几下，还拍出问题了。

处理了一点漏掉的情况，以及解决合并线段树节点出现的笔误，总之就是解决了各种奇奇怪怪的小问题，大样例强度太低了，在结束前半小时调出来了。

至于 C 这个题看起来就脑壳痛，\(60^\circ\) 的基底很难处理，而且坐标有很多限制，没能写出来就结束了。

晚上陪 @c1120241919 和 @LYH_cpp 回酒店，但是走到半路才知道他们已经在酒店里点好了外卖，所以我强制让 @c1120241919 给我推送了附近的餐馆，悠闲吃完了兰州拉面发现只剩十分钟了，遂飞速骑车反超了他们俩。

讲解，笔试题听不懂，老师表示“反正你们以后都要学”。得知了第四题原来是诈骗题，可惜我没有猜答案为 \(0\) 的勇气。

第三题的正常解法是时间复杂度为 \(O(nV)\) 背包，当然还有一个剑走偏锋的做法是仅保留不超过 \(2025\) 的数进行搜索子集和，时间复杂度是 \(O(2^{2025})\)，也就是说他是 \(O(1)\) 的多项式时间做法！

可数集合是可以与自然数集合建立一一对应关系的集合，不是个数可以数出来的集合。简单来讲就是我把可数集合理解成了有限集合。

B 题好像做的略微有点复杂了，不过没关系，能过就行。

8.24

上午机试。

圆环

长度为 \(n\) 的圆环依次编号为 \(1 \sim n\)。

用 \(\frac n 2\) 种颜色给圆环上的 \(n\) 个位置染色：

• 每种颜色恰好染色两个不同的点。
• 同一颜色的两点距离恰好为 \(d\)。

\(A,B\) 两点的距离为 \(\min(\vert A - B \vert, n - \vert A - B \vert)\)。

\(n \le 5 \times 10^5\)。

背包

给定一个大质数 \(p\) 和 \(x \in [0,p)\)。

你需要在集合 \(\{1,2,\dots,5000\}\) 中选择不超过 \(S\) 个依次递增的元素组成序列 \(a_1,a_2,\dots,a_k\)，满足以下条件：

\[\frac{1}{a_1} + \frac{1}{a_2} + \dots + \frac{1}{a_k} \equiv x \pmod{p} \]

可以证明一定在限制条件下一定存在一种方案。

给出这个构造方案。

\(T \le 100, 150 \le S \le 5000, 10^8 \le p \le 10^{18},0 \le x < p\)，\(p\) 是质数。

排序

交互题。

有一个初始为空的序列 \(a\)。

\(n\) 个 \([0,1]\) 均匀随机的实数会依次到来，你不能预先知道后面的数，要将其填充到 \(a\) 序列的一个空位。

你需要实现一个策略，使得 \(\sum\limits_{i=1}^{n-1} \vert a_i - a_{i-1} \vert\) 最小。

对于所有测试点 \(n = 10^5\)，评分方式很神秘，上式小于等于 \(50\) 即可满分。

A 稍微观察了一下官方解法给出的答案文件，直接实现出了和官方解法完全一样的答案，所以直接使用文本比对没有本地写 Special Judge，差不多半个小时通过。

B 毫无头绪，所以先去看 C。

交互题，很显然的策略是将得到的整数 \(x\) 放到位置 \(x \times n\)，因为均匀随机所以期望都能放到对应位置。如果放不下就往后找，后面没有了就往前找。本地交互库获得了 \(40\) 分的好成绩。

做了个优化，前面和后面取预计位置离得最近的，获得了 \(42\) 分。

后面尝试各种奇奇怪怪的策略分段，但是并没有获得更高的分数，然后回去想 B。

尝试了一下随机化直接硬撞，撞不出来。

逆元的性质难以捉摸，用 bitset 跑了一下发现前 \(44\) 个数就可以包含完 \(p \le 10^9\) 的所有情况。

折半写出来以后跑样例花了 8s，然后把值域改成了 \(40\)，又能过了，获得了 \(20\) 分。

然后就是罚坐，尝试进一步提高 C 的分数却没有任何进展。

中午回去吃方便面，晚上再去吃好的。

下午是南京大学软件学院前院长陈道蓄带来的演讲“数智时代”，从最简单的编程问题“1 ~ 9 填充带分数等于 100”，再讲到“dijkstra 最短路算法在现实生活中的局限性”，进一步引出问题“铺砖问题（模拟退火）：启发式算法是否算是一种智能”，最后讲到在当下这个时代我们应该如何学习。总的来说受益匪浅。

然后即是结营仪式，学生分到了两个不同的教室，我妈表示一定是我考的不好才分到了这边，但她拿不出证据。

现任副院长来做宣讲，大致就是介绍学校。颁奖时因为姓名首字母问题是第一批领奖的选手，老师表示本次活动只是体验，和招生不挂钩，所以大家都是参与奖。

活动结束后重返南大记忆文创店，这次给自己买了个可爱立牌，还是要对自己好一点。

晚上参观了酒店隔壁的议事园，然后大吃了一顿，应该是这次来最好吃的一次。

360=20+200+140，出分遗憾离场了，吃了不会笔试的亏，和去年入门级一样高。

创新解题和创意编程，是不是创新有没有创意我不知道，但是真的创人。

@c1120241919 这个笔试 man 372=40+175+157，12 分的差距，就像我的联赛和一等奖的差距，再一次伤感了起来。

和他们俩同一个航班，同时被延误了一个小时，睡眠时间又减少了。

到机场后暗中观察 @c1120241919 打王者荣耀，悄悄地站在他的身旁，他一开始还以为是个小孩子（捂脸。

南京的旅途，就此结束了，这应该也是第一次在一个月内到访同一个外省两次。

在飞机上迁移了一些手机的照片，看着这些照片莫名有些伤感，“怀念过去是不是在时间长河里刻舟求剑”。

迁出去，也算是断了某些思念吧，特别是那些不该耗费我很多时间精力的人和事。

过去未来只是想象中一场美丽电影 小心在梦境太过沉溺

落地时发现登机口编号看着不对劲啊，怎么是 6 开头的，之前从来没见过，难道是新的航站楼？

验证了我的猜想，我们的航班降落于重庆江北国际机场 T3B 航站楼，这是近几个月新修的航站楼，看起来很宏伟很科幻，被帅了一脸。

美中不足就是远了点，乘坐捷运系统（疑似被重庆轨道交通承包的自动驾驶单轨）前往 T3A 主航站楼，这段短暂的单轨旅程让我回忆起了广州的 APM 线。

8.25

还要上课所以直接返回北碚了，到家已然是十二点半，小做收拾后就去睡觉了。

智能机被收缴了，老年机没电了，所以所有闹钟都失效了，然后一觉睡到自然醒，一醒来发现 7:50 了。还好还好，差一点就睡过头了。

后记

总而言之，言而总之，这是一段独一无二且美好的旅程。虽然没有认识很多人，但也收获了很多知识，以后想要报考优秀的高校，还得成为优秀的自己才行。

暑假已接近尾声，所以这篇游记也不会有后续。

敬请期待：CSP-S 2025 游记。