题解 [ARC061E] すぬけ君の地下鉄旅行

题解 [ARC061E] すぬけ君の地下鉄旅行

题意

翻译很清楚，不讲。

分析

首先我们考虑一条线路两两之间都连上一个边权为 $1$ 的点。

很显然空间承受不了。

但是有一个优化技巧叫做建虚点。

建虚点是什么？

建虚点，字面意思上理解来说就是建一个毫不存在的点。

建虚点有什么用？

它可以将类似于一票制的公交线路（即一条线路串联多个点，任意两个点之间的距离或花费相等），减少空间复杂度。

如何建虚点？

首先我们来看这样一个地铁图。（下面的边权指的是公司编号）

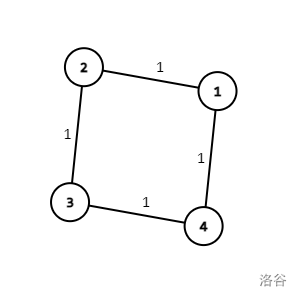
这样的图转化一下就是下面这个样子（边权默认为 $1$）：

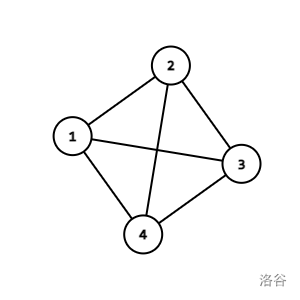
因为是同一个公司下的地铁线路，所以保证两两连边，然后就会像上图一样建很多不必要的边。

但是，我们建一个虚点 $C_1$，所有联通的 $1$ 公司下的点全部连到这个虚点上。

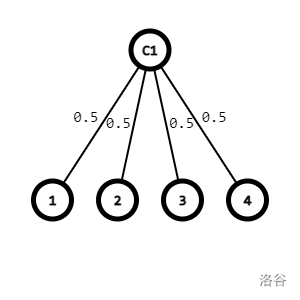
极大节省了空间！而这样同时也保证了联通的同一公司可以互相到达。

我们用同样的方式观察样例 2：

原图：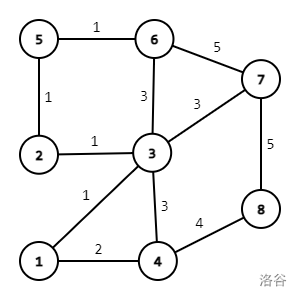

建虚点转化后（边权默认为 $0.5$）：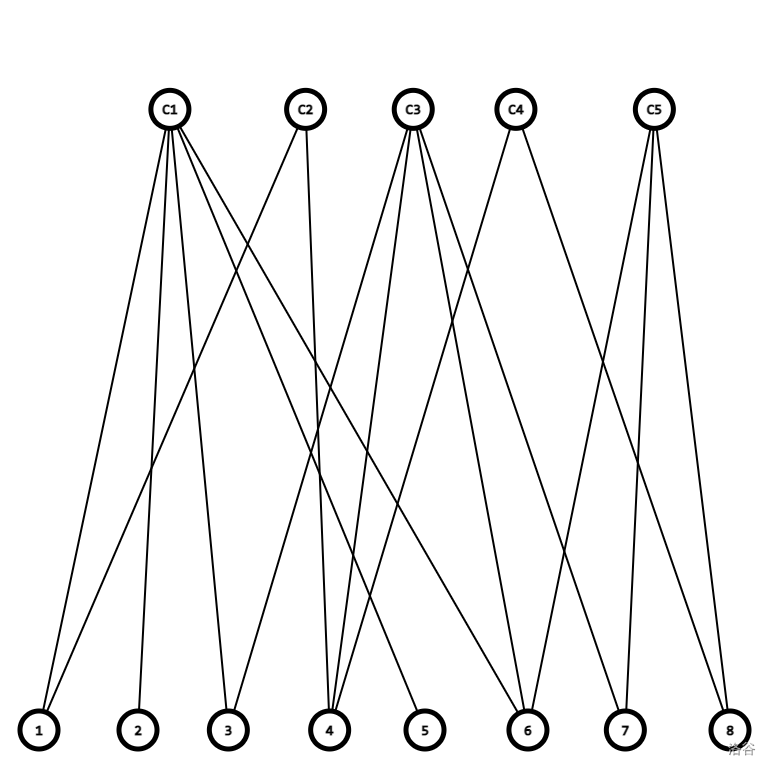

鉴于 $0.5$ 并不是很方便计算，我们直接将边权扩大两倍，计算时答案再缩小 $\dfrac{1}{2}$ 即可。

如何应用到本题上？

用并查集维护联通，如果两条同一个公司的地铁不连通，那么这两条线路无法连接在同一个虚点上！

建虚点后直接 $1 \sim n$ 跑最短路即可。

建虚点的其他练习题

• P7646 [COCI2012-2013#5] HIPERCIJEVI，个人觉得还是比较不错（你从空间限制就看得出来不能直接暴力建图）。

注意事项

• 多测要清空！但是不需要全部清空完，用多少清空多少，否则你会超时整整 $5$ 个点！
• 公司可能有 $10^6$，建虚点的新图过后最坏情况下会有 $N+M$ 个点，请保证你的数组足够。

代码

//the code is from chenjh
#include<cstdio>
#include<cassert>
#include<cstring>
#include<queue>
#include<utility>
#include<vector>
#define MAXN 100001
#define mp std::make_pair
typedef std::pair<int,int> PII;
struct dsu{//并查集。
    public:
        int *fa;
        dsu(int _n=0):n(_n){fa=new int[n+1](),sz=new int[n+1];fa[0]=sz[0]=0;for(int i=1;i<=n;i++)fa[i]=i,sz[i]=1;}//构造函数，初始化并查集。
        inline int* get_fa()const{return fa;}
        inline int* get_sz()const{return sz;}
        dsu&operator = (const dsu&y){if(this!=&y){n=y.size();int*new_fa=new int[n+1]();memcpy(new_fa,y.get_fa(),sizeof(int)*(n+1));delete[] fa;fa=new_fa;int*new_sz=new int[n+1]();memcpy(new_sz,y.get_sz(),sizeof(int)*(n+1));delete[] sz;sz=new_sz;}}
        dsu(const dsu& y){*this=y;}
        ~dsu(){delete[] fa;delete[] sz;}
        inline void clear(){n=0;delete[] fa;fa=new int[n+1]();fa[0]=0;}
        inline void resize(int _n){assert(_n>=0);delete[] fa;delete[] sz;fa=new int[(n=_n)+1]();sz=new int[n+1]();fa[0]=sz[0]=0;for(int i=1;i<=n;i++)fa[i]=i,sz[i]=1;}
        inline int size()const{return n;}
        inline int size(int x)const{assert(0<x && x<=n);return sz[x];}
        inline int find(const int x){assert(0<x && x<=n);return _find(x);}
        inline void merge(int x,int y){assert(0<x && x<=n);assert(0<y && y<=n);x=_find(x),y=_find(y);if(x==y)return;if(sz[x]<sz[y])std::swap(x,y);fa[y]=x,sz[x]+=sz[y];}//按秩合并。
        inline bool same(int x,int y){assert(0<x && x<=n);assert(0<y && y<=n);return _find(x)==_find(y);}
    private:
        int n;
        int*sz;
        inline int _find(const int x){return x==fa[x]?x:fa[x]=find(fa[x]);}//路径压缩。
};
int n,m,t=0;
std::vector<PII> G[1000001];//存储公司的线路。
std::vector<int> E[MAXN<<2];//建虚点后的新图。
int g[MAXN];//这个点对应虚点的编号。
bool vis[MAXN<<2];int dis[MAXN<<2];//是否访问和距离。
int dj(int S,int T){//广搜跑最短路。
    memset(vis,0,sizeof vis);
    std::queue<int> Q;
    memset(dis,0x3f,sizeof dis);
    dis[S]=0;Q.push(S);
    for(int u;!Q.empty();){
        u=Q.front();Q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        if(u==T) return dis[T];
        for(int v:E[u])if(!vis[v] && dis[v]>dis[u]+1) dis[v]=dis[u]+1,Q.push(v);
    }
    return vis[T]?dis[T]:-2;//因为最终答案会除以 2 所以不能到达要返回 -2。
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=0,u,v,w;i<m;i++){
        scanf("%d%d%d",&u,&v,&w);
        G[w].push_back(mp(u,v));//记录 w 公司的线路是 u 到 v。
    }
    dsu d(n);
    for(int i=1;i<=1000000;i++){//枚举每一个公司。
        if(G[i].empty()) continue;
        for(const PII&e:G[i])d.fa[e.first]=e.first,d.fa[e.second]=e.second,g[e.first]=g[e.second]=vis[e.first]=vis[e.second]=0;//用多少清空多少，不要全部清空，否则会超时。
        std::vector<int>v;
        for(const PII&e:G[i]){
            d.merge(e.first,e.second);//合并两个点。
            if(!vis[e.first]) v.push_back(e.first),vis[e.first]=1;//记录被操作过的点。
            if(!vis[e.second]) v.push_back(e.second),vis[e.second]=1;
        }
        for(int j:v)if(d.size(d.find(j))>1){//当前点集的大小要大于 1，否则就是没有被合并过。
            int r=d.find(j);
            if(!g[r]) g[r]=++t;//如果没有建则新建一个虚点。
            int u=n+g[r];
            E[j].push_back(u),E[u].push_back(j);//当前点和虚点连边。
        }
    }
    printf("%d\n",dj(1,n)>>1);
    return 0;
}