图论-最短路
观前提示:建议打开右下角目录配合食用
图论必吃榜之四大三大经典算法:Dijkstra,Bellman-Ford & SPFA,Floyd
(其实SPFA是Bellman-Ford的优化,国际上叫他队列优化的Bellman-Ford,所以就放一块讲了)
还有些进阶的,也放在这讲了:传递闭包、分层建图、环类问题、图上走\(k\)步
此外,蓝书上有些例题也放在这了:洛谷题单:图论-最短路
最后,放几句话在这 qwq
-
不要小瞧某些复杂度较高的算法,他们会在某些特殊题型中大放异彩.
-
图论鄙视链:建模 > 题目特征\思想 > 模板.
-
图论与DP紧密相连,很多图论方法的本质是DP. 务必善用DP思想!
单源最短路
不知道单源最短路是啥的先看眼例题:【模板】单源最短路径(标准版)
\(Dijkstra\)
简介
-
本质是贪心,加上堆优化时间复杂度为\(O(m\ log\ n)\)
-
不能处理有负权边的图,不能判负环
实现
我们用\(dis[x]\)数组记录 ⌈ 从起点到\(x\)的最短路 ⌋ 的长度;\(vis[x]\)记录是否已经过\(x\)点;\(root\)代表起点
-
初始化:\(dis[root]=0,vis[root]=1\),其余dis都为正无穷;并把起点\(root\)加入队列
-
扫描&更新:取出队首,扫描它所有的出边;对于一条边\((u,v,w)\),若\(dis[u]+w<dis[v]\),则说明从\(root\)到\(v\)的最短路长度存在更优解,用\(dis[u]+w\)更新\(dis[v]\)
-
入队&标记:从所有节点中找到未被\(vis\)标记的、\(dis[x]\)最小的节点\(x\),把它加入队列,并用\(vis[x]=1\)标记
重复2、3操作,直至队列为空。
正确性证明:不会证 懒得查资料
堆优化
不难发现,步骤3中 ⌈ 在所有节点中再找一遍最小值 ⌋ 的操作赋予了该算法\(O(n^2)\)的优秀时间复杂度(大嘘
为了不用每次都笨重的再跑一遍\(O(n)\),我们用优先队列,也就是二叉堆来维护这个最小值
具体实现:在步骤2更新的同时,若点\(v\)没有被\(vis\)标记,那么就把\(dis[v]\)和\(v\)加到堆中,利用堆 ⌈ 只对多元组的第一个元素排序 ⌋ 的特点,使得堆顶永远是\(dis\)最小值
那么步骤3就可以省略了,步骤2直接取堆首+标记堆首,完毕
为了方便理解Dij,我整了个图:
时间复杂度:\(O(m\ log\ n)\)
Code
使用Linklist存图(豪用😋)
(注:我的head数组初始值设为-1,所以扫描出边时是以~i为判定)
int dis[N],vis[N],root;
priority_queue<pair<int,int> > q; //默认从大到小排序!first是dis[v],second是节点v
void dijkstra()
{
dis[root]=0;
q.push({0,root});
while(!q.empty()){
int u=q.top().second; //取堆顶
q.pop();
if(vis[u]) continue; //不是我喜欢的点,直接跳过!
vis[u]=1; //标记
for(int i=head[u];~i;i=e[i].next){ //扫描出边
int v=e[i].v;
if(dis[u]+e[i].w<dis[v]){ //更新
dis[v]=dis[u]+e[i].w;
if(!vis[v]) q.push({-dis[v],v}); //取负进堆,实现从小到大排序awa
}
}
}
}
\(Bellman-Ford\ \&\ SPFA\)

(NOI2018 Day 1,T1 出题人卡了 SPFA 并在讲课时宣布SPFA已死)
(此事在例题题面中亦有记载)
感觉现在的出题人已经把 ⌈ 随手卡一下SPFA ⌋ 当成业界常识了;
还有很多dalao们想出很多优化方法来挽救SPFA(LLL、SLF等),都被Hack掉了
所以不是负权图就谨慎使用SPFA吧(反正我刚学awa)
简介
-
Bellman-Ford基于迭代思想,时间复杂度\(O(nm)\)
-
SPFA是Bellman-Ford的队列优化形式,复杂度\(O(km)\)(\(k\)是一个较小的常数)
但容易被卡,退化为Bellman-Ford的\(O(nm)\)(标准版模板就过不了)
-
可处理负权边,可用来判负环(但跑不了负环,有负环还能有最短路吗:P )
实现
Bellman-Ford:
- 扫描所有边\((u,v,w)\),若\(dis[u]+w>dis[v]\),就用\(dis[u]+w\)更新\(dis[v]\)
- 重复步骤1,直至没有边可再被更新
SPFA优化:
-
建一个队列,初始把起点\(root\)加入队列
-
取出队首\(x\),扫描所有出边,用\(dis[x]+w>dis[v]\)更新\(dis[v]\).同时,若\(v\)不在队列中,就把\(v\)入队
-
重复步骤2,直至队列为空
具体地,用一个\(vis\)维护队列中的元素,取出队首\(x\)时\(vis[x]=0\)
实际上SPFA就是优化了Bellman-Ford暴力枚举中 ⌈ 重复扫描的冗余节点 ⌋.
懒得整图了
Code
(总觉得SPFA代码和Dijkstra好像,是错觉吗 更好记了awa)
int dis[N],vis[N],root;
queue<int> q;
void spfa()
{
dis[root]=0;
q.push(root);
while(!q.empty()){
int u=q.front();
q.pop();
vis[u]=0; //队首出队
for(int i=head[u];~i;i=e[i].next){ //熟悉的扫描
int v=e[i].v;
if(dis[u]+e[i].w < dis[v]){ //熟悉的判定
dis[v]=dis[u]+e[i].w;
if(!vis[v]) q.push(v),vis[v]=1; //入队并标记为队内元素
}
}
}
}
为什么SPFA可处理负权图,而Dij不行?
这个问题看似很容易,找个负权图反例来hack Dij (不含负环!)
但其实我自造的负权图和网上的反例都被Dij干趴下了(汗
最后是Cornessless大佬用随机图+SPFA对拍才找出来一组(%%%
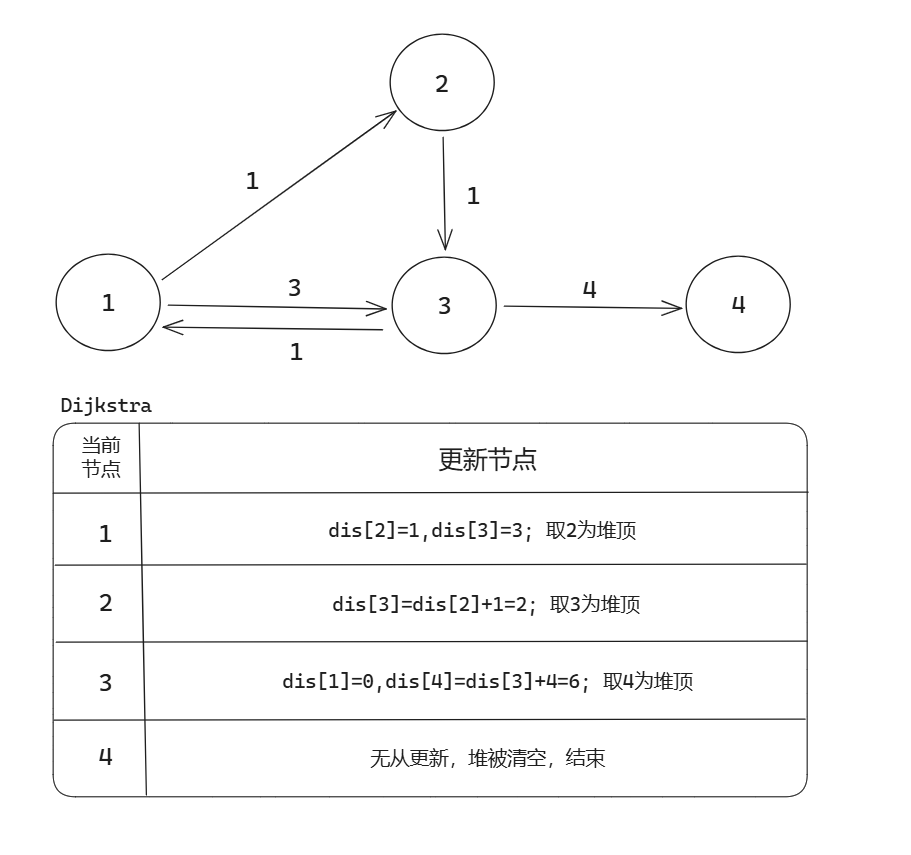
Finally,被简化成了这张图:

开始时Dij会先让3号点成为堆顶,此时\(dis[3]=1\);
然后从3用 ⌈ \(dis[3]+1\) ⌋ 更新\(dis[4]\) ,\(dis[4]=1+1=2\) ;并给3打上\(vis\)标记
但\(dis[3]\) 后来被2更新成更小,即从2开始更新时有\(dis[3]=dis[2]-2=0\)
可\(dis[3]\) 已经被\(vis\)标记过了,也就是说不会再从3更新\(dis[4]\)
那么最后就有了\(dis[4]=2\)这个错误答案.
这便是贪心的性质:择优前进,不回头
而SPFA中,由于它每次更新时都会把 ⌈ 可更新的节点 ⌋ 再次加入队列
那么3号节点就会再次入队并更新\(dis[4]\),得出\(dis[4]=1\)的正确答案.
任意两点间最短路(多源最短路)
老样子,先看例题【模板】Floyd
\(Floyd\)
简介
-
其本质是DP,在\(O(n^3)\)的时间复杂度内处理任意两点间的最短路
且需要开邻接矩阵,空间复杂度\(O(n^2)\),因此多用于N比较小的稠密图中.
-
可处理负权边,不能判负环
实现
因为其本质是DP,所以我们多讲一点有关DP的东西qwq
设\(f[k,i,j]\)表示 ⌈ 经过若干个编号不超过\(k\)的节点 ⌋ 从\(i\)到\(j\)的最短路长度,
那么\(f[k,i,j]\)可被划分为两个子问题:⌈ 经过若干个编号不超过\(k-1\)的节点 从\(i\)到\(j\) ⌋,或者 ⌈ 在经过编号不超过\(k-1\)的基础上,从\(i\)先到\(k\) 再到\(j\) ⌋.
写成状态转移方程就是:
\(f[k,i,j]=min(f[k-1,i,j]\ ,\ f[k-1,i,k]+f[k-1,k,j])\)
以上是抄书,不理解也没事,再举个🍳的栗子awa

很明显,1 -> 4 的最短路径是 1 -> 3 -> 2 -> 4 ; 我们可以把3、2理解为中转站
当\(k=1\)时,我们只能把1当作中转站;此时\(f[1,1,4]\) (也就是1 -> 4 的距离)=10(初始路径)
当\(k=2\)时,我们能把1、2当作中转站;此时虽然从1 到不了2 ,但我们可更新3 -> 2 -> 4,距离为2,明显要比\(f[1,3,4]=5\)要小,那么\(f[2,3,4]=min(f[1,3,4]\ ,\ f[1,3,2]+f[1,2,4])=2\)
如此拓展,\(k=3\)时有\(f[3,1,4]=min(f[2,1,4]\ ,\ f[2,1,3]+f[2,3,4])=3\)
那么我们仿照背包的一维优化,用滚动数组代替\(k\)这一维,就有了以下方程:
\(f[i,j]=min(f[i,j]\ ,\ f[i,k]+f[k,j])\)
特别的,由于是邻接矩阵,所以在memset成inf之后记得有\(f[i,i]=0\).
Code
说了这么多,其实Floyd的核心算法只有五行qwq (DP特有的用一天时间想一行代码)
但如果你听懂了我将不胜感激awa
对了:因为\(k\)代表阶段,所以\(k\)层循环必须放在最外层!!
for(int k=1;k<=n;k++) //进食后人:放内层会WA
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
进阶算法\技巧
Floyd进阶:传递闭包
传递闭包简介
⌈ 传递闭包 ⌋ 这个词看着挺难懂,实际上就是描述了一种关系:传递性.
没错,就是你想的那个传递性:若有\(a<b,b<c\),则有\(a<c\)
传递闭包的完整定义:⌈ 通过传递性推导出尽量多的元素之间的关系 ⌋ 的问题叫做传递闭包.
放在图论里,它更多描述的是两点之间是否联通:若A与B相联通,B与C联通,则可推出A与C联通
我们把B看作Floyd中的 ⌈ 中转站 ⌋,便可用Floyd解决传递闭包问题.
对了,先撂个模板题在这:【模板】传递闭包
用Floyd解决传递闭包
具体的,\(f[i,j]=1\)表示i与j有关系(联通),\(f[i,j]=0\)表示i与j莫得关系(不连通).
Specially,\(f[i,i]\)始终为1. (但模板题不一样,不需要\(f[i,i]=1\),原因不明)
如果\(f[i,k]\ \&\ f[k,j]=1\),说明\(i,j\)可通过\(k\)作为中转站联通
如果\(f[i,k]\ \&\ f[k,j]=0\),但\(f[i,j]=1\),说明\(i,j\)仍联通,只不过无法通过\(k\)联通.
那么就有了以下方程:
\(f[i,j]\ |=f[i,k]\ \&\ f[k,j]\)
朴素のCode:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
f[i][j]|=f[i][k]&f[k][j];
}
复杂度仍为\(O(n^3)\). 能Better吗?
Bitset优化
我们可以把上面的方程拆成两步:先判断\(f[i,k]\)是否为1; 若成立,则直接用\(f[k,j]\) 或上\(f[i,j]\).
这样,若\(f[k,j]=1\),则可更新\(f[i,j]=1\);若\(f[k,j]=0\),那么\(f[i,j]\)保持原状态.
写成代码就是:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(!f[i][k]) continue;
f[i][j]|=f[k][j];
}
既然 \(f[i,j]\) 只用存 \(0\ or\ 1\),且又有位运算,那么......
Bitset优化,启动!
用Bitset可直接对 \(j\) 这一维进行位运算,我们可以删去 \(j\) 层的循环!
复杂度\(O(n^2)\),完全胜利✌
最终Code
bitset<N> f[N];
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++){
if(!f[i][k]) continue;
f[i]|=f[k];
}
分层建图
实际上分层建图不算是一种算法,更多的是一种建模思想;建完模直接溜最短路模板即可.
然而,正如开头的鄙视链,建模往往是最难的.
下面来详细介绍一下分层建图的思想.
直接应用
相当于分层建图的模板,初步了解下分层建图的运作方式.
它解决的是这样一类问题:允许你改变\(K\)条边的权值(免费、打折),再让你求最短路(多是单源最短路)
(自己打了半天解释感觉不如题解dalao的一幅图+一句话,故放这了)

建\(k+1\)层图;各层内部正常连边,各层之间从上到下连权值为0的边。每向下跑一层,就相当于免费过一条边。跑一遍从起点到\((k+1)n\)(在上图中就是1到9)的最短路即可。
建分层图代码如下:
for(int i=1;i<=m;i++){
int x,y,z;
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
for(int j=1;j<=k;j++){
add(x+(j-1)*n,y+j*n,0);
add(y+(j-1)*n,x+j*n,0); //连接上下层
add(x+j*n,y+j*n,z);
add(y+j*n,x+j*n,z); //2~k层内的正常连边
}
}
结合DP
还记得开头的另一句话吗?很多图论方法的本质是DP;请务必善用DP思想.
分层建图的本质也是DP. 向下跑一层,就是从当前状态转移到下一个状态.
不难发现,上述的题型亦是如此:向下跑一层代表从 ⌈ 已用\(k\)张打折 ⌋ 转移到 ⌈ 已用\(k+1\)张打折 ⌋.
找到题目中潜藏的状态描述是关键. 比如下面两个例题:
这题经分析后有三个状态:⌈ 买入物品前 ⌋、⌈ 已买入但还未卖出 ⌋、⌈ 卖出后 ⌋.
那么我们可以建三层图分别代表这3种状态,每向下转移一层就代表进入下一个状态.

如图,层1 -> 层2代表买入,边权为负;层2 -> 层3代表卖出,边权为正.
最终求的是图中两个绿点的最短路.
负权?就决定是你了,SPFA!
关于这题我有个非常抽象的经历 (整活)
显然,这题的路线也有两个状态:⌈ 横向走 ⌋ or ⌈ 纵向走 ⌋;而中转站可切换这个状态.
那么我们可以建两层图:层1代表横向时有哪些中转站能互相抵达,边权为\(2\times\)两站横向距离; 层2代表纵向. 上下层间垂直连边权为1的边,表示切换方向的费用.
记得把起点和终点也纳入图中!
这次就不画图了awa
环类问题
SPFA判负环
虽然SPFA跑不了负环图,但它可以判啊!
首先,在负环图上跑最短路是没有结果的,算法会一直绕着负环跑(因为\(dis\)可被不断更新)
但若是正常的无负环图,它的最短路径上不会存在超过\(n\)个节点.
否则至少有一个结点被重复经过,这说明存在环,且经过该环能更新该结点的\(dis\)值,即存在负环.
所以:如果一个节点进队超过\(n\)次,那么说明存在从起点到达的负环.
(上两句不是我说的,详见原文,解释得比我清楚多了QAQ)
放个模板在这:【模板】负环
最小环
最小环的定义:给定一张无向\有向图,求图中一个至少包含 3 个点的环,环上的节点不重复,并且环上的边的长度之和最小.
- 对于有向图,直接枚举1~n的点,跑n次Dijkstra;对于每次的起点\(i\),在扫描完所有出边后把 \(dis[i]\) 更新为 \(inf\) ,这样等\(i\)第二次进堆时,\(dis[i]\) 就是经过点\(i\)的最小环长度.
- 对于无向图,我从例题 Sightseeing trip 出发,所以附带一个求无向图最小环路径的方法awa
考虑Floyd (别问为什么不用Dij,问就是没找到)
在Floyd算法枚举 \(k\) 的时候,已经得到了前 \(k−1\) 个点中每两个点的最短路径,这 \(k−1\) 个点不包括点 \(k\) ,并且他们的最短路径中也不包括 \(k\) 点.
那么我们便可以从这前 \(k−1\) 个点中选出两个点 \((i,j)\) 来,因为 \(dis[i,j]\)已经是此时 \((i,j)\) 间的最短路径,且这个路径不包含 \(k\) 点.
所以连接 \(i→j→k→i\) ,我们就得到了一个经过 \((i,j,k)\) 的最小环.
(摘自题解↑)
至此已可以求出最小环长度. 可路径呢?
需注意一点,连接 \(i→j→k→i\) 时,\(j→k→i\) 这一部分是确定的;但由于 \(i→j\) 是由 \(dis[i,j]\) 直接转移过来的,具体路径并不清楚,所以上式实际上是这样:
\(i→...→j→k→i\)
这个 ⌈ ... ⌋ 便是此前原版Floyd所用的中转点 \(k\).
那在原版Floyd进行状态转移 ⌈ \(dis[i,j]=dis[i,k]+dis[k,j]\) ⌋ 时,顺便用一个 \(pos[i,j]\) 记录 \(k\) ,代表 \(dis[i,j]\) 由 \(dis[i,k]+dis[k,j]\) 转移而来,路径为 \(i→...→k→...→j\)
那么我们可以由此递归求出 \(i→j\) 的路径啦!Bingo!
递归求路径代码:
vector<int> path;
void get_path(int x,int y)
{
if(!pos[x][y]) return; //若pos[x,y]=0,说明x→y即为最短路径
get_path(x,pos[x][y]);
path.push_back(pos[x][y]);
get_path(pos[x][y],y);
}
Floyd求最小环代码(含记录路径):
//由于是blog就浅压一下行awa
void floyd()
{
for(int k=1;k<=n;k++){
for(int i=1;i<k;i++) //求最小环&记录路径
for(int j=i+1;j<k;j++)
if(ans>(ll)dis[i][j]+a[j][k]+a[k][i]){ //由于dis & a可能是inf,所以开ll
ans=dis[i][j]+a[j][k]+a[k][i]; //这里的a就是最初的邻接矩阵(原始图)
path.clear(); //答案被更新,路径发生改变!
path.push_back(i);
get_path(i,j);
path.push_back(j);
path.push_back(k);
}
for(int i=1;i<=n;i++) //原版Floyd
for(int j=1;j<=n;j++)
if(dis[i][j]>dis[i][k]+dis[k][j]){
dis[i][j]=dis[i][k]+dis[k][j];
pos[i][j]=k;
}
}
}
图上走 \(K\) 步
同样先放个例题:[USACO07NOV] Cow Relays G
题意:给定一张 \(T\) 条边的无向连通图,求从 \(s\) 到 \(t\) 经过 \(K\) 条边的最短路长度
本来打了很多思路,但编不下去了QAQ 遂来开门见山
我们用矩阵快速幂解决这类问题. 矩阵乘法&快速幂部分详见我的另一篇blog: 快速幂,这里只讲如何解决.
首先,邻接矩阵也是矩阵 (名字都写了). 我们可将原始矩阵A看作两点间经过1条边的最短路.
对于一点对 \((i,j)\) ,我们枚举一个中转点 \(k\) ,考虑下列公式:
$B[i,j]={\underset{1\leq k \leq n}{min}} \lbrace A[i,k]+A[k,j] \rbrace $
这样就有了\(i→k→j\)这个最短路路径. 因此,\(B[i,j]\)表示 \((i,j)\) 经过2条边的最短路
发现没?上述公式和矩阵乘法公式有些许相似:
\(C[i,j]=\sum_{k=1}^n \lbrace A[i,k]+B[k,j] \rbrace\)
因为 \(min\) 运算也满足结合律,所以第一个公式可以被看作广义的矩阵乘法.
而对于走 \(K\) 步,我们只需要枚举 \(K\) 次 \(k\),也就是做 \(K\) 次改版的矩阵乘法.
这不就是矩阵快速幂吗?直接套板子!
但要注意:乘法中初始化矩阵时,由于是 \(min\) 运算所以要全部设为 \(inf\) !
//如此建结构体!
struct Matrix{
int a[N][N];
Matrix() { memset(a,0x3f,sizeof(a)); }
inline int* operator [](const int i) {
return a[i];
}
}dis;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号