2024 山东省夏令营高算班【讲课】

Day 1 数论

数论入门

欧几里得算法

若 \(a\perp b\)，则 \(\gcd(a^m-b^m,a_n-b^n)=a^{\gcd(n,m)}-b^{\gcd(n,m)}\)，证明用辗转相减做到指数上。

若 \(n^a\equiv 1(\mod m)\) 且 \(n^b\equiv 1(\mod m)\)，则 \(n^{\gcd(a,b)}\equiv 1(\mod m)\)，同理可证。

[CF1656H]EQUAL LCM SUBSETS

插入困难, 我们考虑从全集中删数: 如果对于一个数字的某一个质因子, 如果它的指数大于对方集合中任意一个数相同质因子的最大指数, 那这个数一定不可能存在, 直接删掉。删完后就是合法的了。

值域不允许质因子分解。

然后呢?……

上线段树不会/cf

基于值域预处理的快速 \(\gcd\)

引理：对于任意整数 \(n\)，存在一种划分方式 \(n=abc\)，其中 \(a,b,c\) 三数要么是质数，要么 \(\le \sqrt n\)。

裴蜀定理

若 \(ax+by=m\) 有解，当且仅当 \(\gcd(a,b)|m\)。

扩展欧几里得算法

矩阵表示形式没听。

VJUDGE BAEKJOON-19523

每条副对角线（取模意义下）的状态必然相同，条数为 \(g=\frac{hw}{lcm(h,w)}=\gcd(h,w)\)。证明为设 \(d\) 为一条副对角线上的点的数量，所以 \(x+d\equiv x(\mod h),y-d\equiv y(\mod w)\)，所以 \(d\equiv 0(\mod h),d\equiv 0(\mod w)\)，可得 \(d=lcm(h,w)\)，即可得所求条数。

因此我们只需确定这 \(g\) 条对角线的值，最后的操作序列自然是 \(a_0 a_1 \dots a_{g-1} a_0 a_1 \dots\)。

不考虑内部状态的具体顺序，最后组合数处理一下即可。

不妨设序列 \({a}\) 中有 \(k\) 个 \(R\)，\(g-k\) 个 \(D\)，那么一个点 \((X,Y)\) 会走到 \((X+(g-k),Y+k)\)，那么产生这种情况当且仅当存在一个 \(x\) 使得 \(x<\frac{hw}{g}\) 且 \(h|x(g-k),w|xg\)，注意到这等价于寻找最小的 \(x\)，判断其是否小于 \(\frac{hw}{g}\)，于是条件等价于 \(x=lcm(\frac{h}{\gcd(d-k,h)},\frac{w}{\gcd(w,k)})\)，枚举 \(k\) 并判断即可。

几个《具体数学》上的简单例题

• Problem 1

• Problem 2

同余

基本性质

威尔逊定理

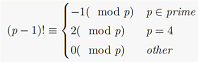
费马小定理

若 \(n\perp p\) 且 \(p\) 为质数，则 \(n^{p-1}\equiv 1(\mod p)\)。

不记了，我的评价是不如去看 早期数学笔记。

Day 2 可持久化数据结构

可持久化线段树

P3834 【模板】可持久化线段树 2

首先考虑静态全局第 \(k\) 小，可以用权值线段树，在线段树上二分，同时也支持动态全局第 \(k\) 小（单点修改）。

考虑静态区间第 \(k\) 小，对于每个前缀 \(a_{1,2,\dots,n}\) 都建一个权值线段树 \(T_i\)，\(T_i\) 中代表区间 \([l,r]\) 的节点存前缀 \(a_{i,2,\dots,n}\) 中有多少个数在 \([l,r]\) 内。

对于 \([l,r]\) 的询问，我们只需将 \(T_r\) 与 \(T_{l-1}\) 两棵树中的对应节点相减，就得到了该区间的权值线段树。

但一共需要 \(O(n^2)\) 个节点，考虑优化。

发现 \(T_i\) 较 \(T_{i-1}\) 只修改了从 \(a_i\) 对应的叶子节点到根节点的路径上的权值，共 \(O(\log n)\) 个节点。

因此，从 \(T_{i-1}\) 到 \(T_i\) 的过程中，我们只需要新建发生变化的 \(O(\log n)\) 个节点，剩下的节点与 \(T_{i-1}\) 共用（即新建根节点，被修改的儿子新建节点，未被修改的儿子仍用 \(T_{i-1}\) 的）。

区间修改同理，同样只有 \(O(\log n)\) 个节点被修改。