PCA与白化，深度学习入门---PCA，白化

深度学习入门---PCA，白化_pca白化-CSDN博客

引言

主成分分析（PCA）是一种能够极大提升无监督特征学习速度的数据降维算法。更重要的是，理解PCA算法，对实现白化算法有很大的帮助，很多算法都先用白化算法作预处理步骤。
假设你使用图像来训练算法，因为图像中相邻的像素高度相关，输入数据是有一定冗余的。具体来说，假如我们正在训练的16x16灰度值图像，记为一个256维向量 x∈R256x∈ℜ256，其中特征值 xjxj 对应每个像素的亮度值。由于相邻像素间的相关性，PCA算法可以将输入向量转换为一个维数低很多的近似向量，而且误差非常小。

假设我们拥有数据{x(1),x(2),…,x(m)}{x(1),x(2),…,x(m)}，维度n=2n=2，即x(i)∈R2x(i)∈ℜ2。假设我们想把数据从2维降到1维。（在实际应用中，我们也许需要把数据从256维降到50维；在这里使用低维数据，主要是为了更好地可视化算法的行为）。下图是我们的数据集：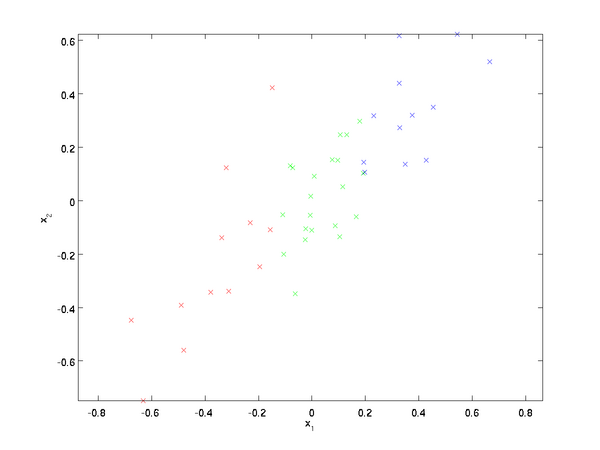

这些数据已经进行了预处理，使得每个特征 x1x1和 x2x2具有相同的均值（零）和方差。
为方便展示，根据x1x1值的大小，我们将每个点分别涂上了三种颜色之一，但该颜色并不用于算法而仅用于图解。
PCA算法将寻找一个低维空间来投影我们的数据。从下图中可以看出，u1u1是数据变化的主方向，而 u2u2 是次方向

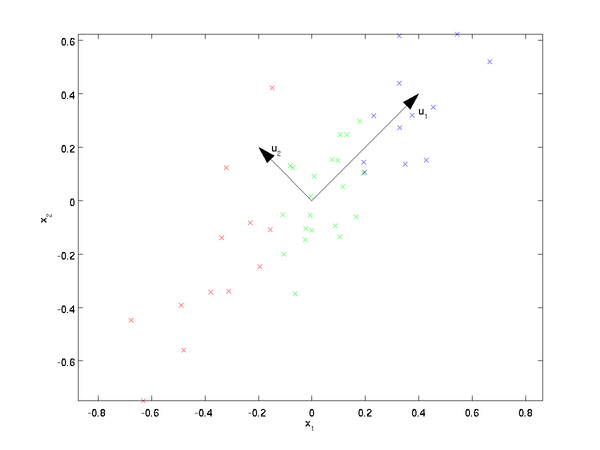
也就是说，数据在u1u1方向上的变化要比在 u2u2方向上大。为更形式化地找出方向 u1u1和 u2u2 ，我们首先计算出矩阵 ΣΣ ，如下所示：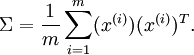

实际上在代码实现时，上面的x(i)x(i)对应是全部数据集，样本按列摆放。

假设xx的均值为零，那么ΣΣ 就是x的协方差矩阵。（符号 ΣΣ，读”Sigma”，是协方差矩阵的标准符号。虽然看起来与求和符号 ∑ni=1i∑i=1ni比较像，但它们其实是两个不同的概念。）

可以证明，数据变化的主方向 u1u1就是协方差矩阵 ΣΣ 的主特征向量，而 u2u2是次特征向量。

求得协方差矩阵后，我们需要求出其对应的特征向量组成的矩阵U，按列摆放。

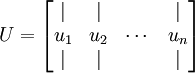
此处，u1u1是主特征向量（对应最大的特征值），u2u2是次特征向量。以此类推，另记 λ1,λ2,…,λnλ1,λ2,…,λn为相应的特征值。
在本例中，向量 u1和u2u1和u2构成了一个新基，可以用来表示数据。令x∈R2x∈ℜ2为训练样本，那么 uT1xu1Tx 就是样本点 xx在维度u1u1上的投影的长度（幅值）。同样的， uT2xu2Tx是xx投影到 u2u2维度上的幅值。

旋转数据

至此，我们可以把 xx用(u1,u2)(u1,u2) 基表达为：

 

xrot=UTx=[uT1xuT2x]xrot=UTx=[u1Txu2Tx]

（下标“rot”来源于单词“rotation”，意指这是原数据经过旋转（也可以说成映射）后得到的结果）

对数据集中的每个样本 ii分别进行旋转： x(i)rot=UTx(i)xrot(i)=UTx(i) for every ii，然后把变换后的数据 xrotxrot显示在坐标图上，可得：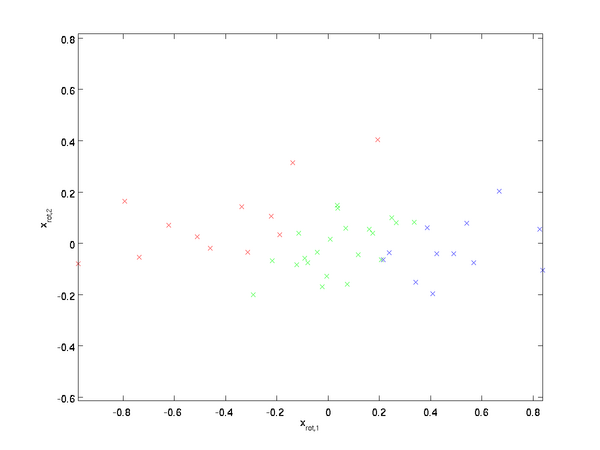

这就是把训练数据集旋转到 u1，u2u1，u2基后的结果。一般而言，运算 UTxUTx表示旋转到基 u1,u2,...,unu1,u2,...,un之上的训练数据。矩阵 UU有正交性，即满足 UTU=UUT=IUTU=UUT=I，所以若想将旋转后的向量 xrotxrot还原为原始数据xx，将其左乘矩阵UU即可： x=Uxrotx=Uxrot , 验算一下：Uxrot=UUTx=x.Uxrot=UUTx=x.

数据降维

数据的主方向就是旋转数据的第一维 xrot,1xrot,1 。因此，若想把这数据降到一维，可令：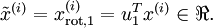

更一般的，假如想把数据 x∈Rn降到kx∈ℜn降到k维表示 x~∈Rk（令k<n）x~∈ℜk（令k<n）,只需选取xrotxrot的前 kk个成分，分别对应前kk个数据变化的主方向。

PCA的另外一种解释是：xrotxrot是一个 nn 维向量，其中前几个成分可能比较大（例如，上例中大部分样本第一个成分x(i)rot,1=uT1x(i)xrot,1(i)=u1Tx(i)的取值相对较大），而后面成分可能会比较小（例如，上例中大部分样本的 x(i)rot,2=uT2x(i)xrot,2(i)=u2Tx(i)较小）。

PCA算法做的其实就是丢弃 xrotxrot中后面（取值较小）的成分，就是将这些成分的值近似为零。具体的说，设 x~是xrotx~是xrot的近似表示，那么将 xrotxrot除了前 kk个成分外，其余全赋值为零，就得到：

 

x~=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢xrot,1⋮xrot,k0⋮0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥≈⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢xrot,1⋮xrot,kxrot,k+1⋮xrot,n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=xrotx~=[xrot,1⋮xrot,k0⋮0]≈[xrot,1⋮xrot,kxrot,k+1⋮xrot,n]=xrot

在本例中，可得x~x~的点图如下（取 n=2,k=1n=2,k=1）：

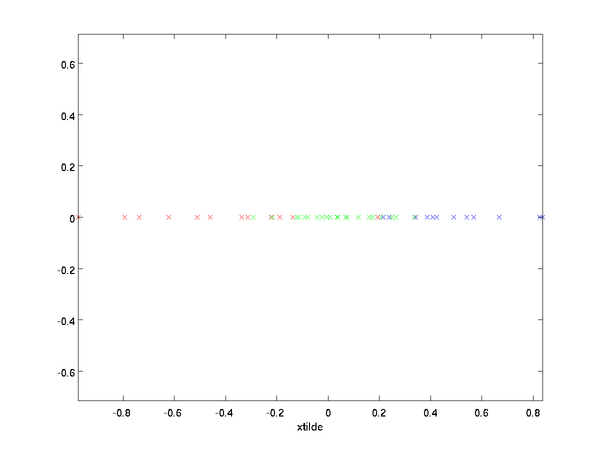
然而，由于上面 x~的后n−kx~的后n−k项均为零，没必要把这些零项保留下来。所以，我们仅用前 kk个（非零）成分来定义 kk维向量 x~x~。

这也解释了我们为什么会以u1,u2,…,unu1,u2,…,un为基来表示数据：要决定保留哪些成分变得很简单，只需取前 kk个成分即可。这时也可以说，我们“保留了前 kk个PCA（主）成分”。

还原近似数据

现在，我们得到了原始数据x∈Rnx∈ℜn的低维“压缩”表征量 x~∈Rkx~∈ℜk ， 反过来，如果给定 x~x~，我们应如何还原原始数据xx 呢？查看以往章节以往章节可知，要转换回来，只需 x=Uxrotx=Uxrot即可。进一步，我们把 x~x~看作将 xrotxrot的最后 n−kn−k个元素被置0所得的近似表示，因此如果给定x~∈Rkx~∈ℜk，可以通过在其末尾添加n−k个0n−k个0来得到对xrot∈Rnxrot∈ℜn 的近似，最后，左乘 UU便可近似还原出原数据 xx 。具体来说，计算如下：

 

x^=U⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢x~1⋮x~k0⋮0⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥=∑i=1kuix~i.x^=U[x~1⋮x~k0⋮0]=∑i=1kuix~i.

上面的等式基于先前对 \textstyle U 的定义。在实现时，我们实际上并不先给 x~x~ 填0然后再左乘 UU，因为这意味着大量的乘0运算。我们可用 x~∈Rkx~∈ℜk来与UU 的前 kk列相乘，即上式中最右项，来达到同样的目的。将该算法应用于本例中的数据集，可得如下关于重构数据 x^x^的点图：

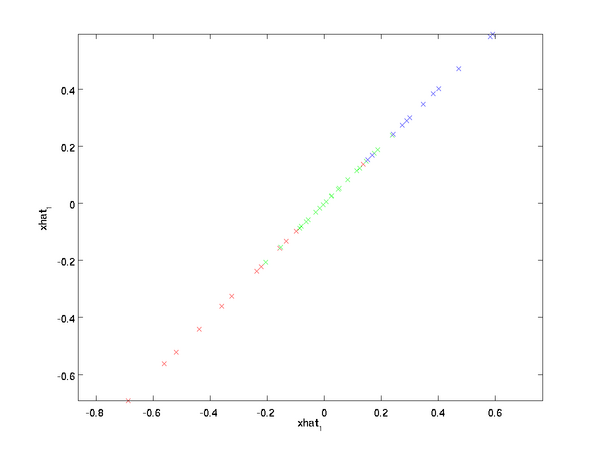
由图可见，我们得到的是对原始数据集的一维近似重构。
在训练自动编码器或其它无监督特征学习算法时，算法运行时间将依赖于输入数据的维数。若用x~∈Rkx~∈ℜk 取代xx 作为输入数据，那么算法就可使用低维数据进行训练，运行速度将显著加快。对于很多数据集来说，低维表征量x~x~是原数据集的极佳近似，因此在这些场合使用PCA是很合适的，它引入的近似误差的很小，却可显著地提高你算法的运行速度。

选择主成分个数

我们该如何选择 kk ，即保留多少个PCA主成分？在上面这个简单的二维实验中，保留第一个成分看起来是自然的选择。对于高维数据来说，做这个决定就没那么简单：如果 kk 过大，数据压缩率不高，在极限情况k=nk=n时，等于是在使用原始数据（只是旋转投射到了不同的基）；相反地，如果 kk过小，那数据的近似误差太太。
决定 kk值时，我们通常会考虑不同 kk值可保留的方差百分比。具体来说，如果 k=nk=n，那么我们得到的是对数据的完美近似，也就是保留了100%的方差，即原始数据的所有变化都被保留下来；相反，如果k=0k=0 ，那等于是使用零向量来逼近输入数据，也就是只有0%的方差被保留下来。
一般而言，设 λ1,λ2,…,λnλ1,λ2,…,λn表示 ΣΣ的特征值（按由大到小顺序排列），使得 λjλj为对应于特征向量ujuj的特征值。那么如果我们保留前 kk个成分，则保留的方差百分比可计算为：

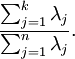
在上面简单的二维实验中，λ1=7.29，λ2=0.69。λ1=7.29，λ2=0.69。因此，如果保留 k=1k=1个主成分，等于我们保留了7.29/(7.29+0.69)=0.9137.29/(7.29+0.69)=0.913，即91.3%的方差。
对保留方差的百分比进行更正式的定义已超出了本教程的范围，但很容易证明，λj=∑mi=1x2rot,jλj=∑i=1mxrot,j2。因此，如果 λj≈0，则说明xrot,jλj≈0，则说明xrot,j也就基本上接近于0，所以用0来近似它并不会产生多大损失。这也解释了为什么要保留前面的主成分（对应的λjλj值较大）而不是末尾的那些。 这些前面的主成分 xrot,jxrot,j变化性更大，取值也更大，如果将其设为0势必引入较大的近似误差。
以处理图像数据为例，一个惯常的经验法则是选择 \textstyle k 以保留99%的方差，换句话说，我们选取满足以下条件的最小 kk值：

 

∑kj=1λj∑nj=1λj≥0.99.∑j=1kλj∑j=1nλj≥0.99.

对其它应用，如不介意引入稍大的误差，有时也保留90-98%的方差范围。若向他人介绍PCA算法详情，告诉他们你选择的 kk保留了95%的方差，比告诉他们你保留了前120个（或任意某个数字）主成分更好理解。

对图像数据应用PCA算法

为使PCA算法能有效工作，通常我们希望所有的特征x1,x2,…,xnx1,x2,…,xn都有相似的取值范围（并且均值接近于0）。如果你曾在其它应用中使用过PCA算法，你可能知道有必要单独对每个特征做预处理，即通过估算每个特征 xjxj的均值和方差，而后将其取值范围规整化为零均值和单位方差。但是，对于大部分图像类型，我们却不需要进行这样的预处理。假定我们将在自然图像上训练算法，此时特征 xjxj 代表的是像素jj的值。所谓“自然图像”，不严格的说，是指人或动物在他们一生中所见的那种图像。
注：通常我们选取含草木等内容的户外场景图片，然后从中随机截取小图像块（如16x16像素）来训练算法。在实践中我们发现，大多数特征学习算法对训练图片的确切类型并不敏感，所以大多数用普通照相机拍摄的图片，只要不是特别的模糊或带有非常奇怪的人工痕迹，都可以使用。
在自然图像上进行训练时，对每一个像素单独估计均值和方差意义不大，因为（理论上）图像任一部分的统计性质都应该和其它部分相同，图像的这种特性被称作平稳性（stationarity）。
具体而言，为使PCA算法正常工作，我们通常需要满足以下要求：(1)特征的均值大致为0；(2)不同特征的方差值彼此相似。对于自然图片，即使不进行方差归一化操作，条件(2)也自然满足，故而我们不再进行任何方差归一化操作（对音频数据,如声谱,或文本数据,如词袋向量，我们通常也不进行方差归一化）。实际上，PCA算法对输入数据具有缩放不变性，无论输入数据的值被如何放大（或缩小），返回的特征向量都不改变。更正式的说：如果将每个特征向量 xx都乘以某个正数（即所有特征量被放大或缩小相同的倍数），PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化，唯一还需进行的规整化操作就是均值规整化，其目的是保证所有特征的均值都在0附近。根据应用，在大多数情况下，我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中，图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说，我们对图像块的平均亮度值不感兴趣，所以可以减去这个值来进行均值规整化。
具体的步骤是，如果 x(i)∈Rnx(i)∈ℜn代表16x16的图像块的亮度（灰度）值（n=256n=256），可用如下算法来对每幅图像进行零均值化操作：
μ(i):=1n∑nj=1x(i)jμ(i):=1n∑j=1nxj(i)
x(i)j:=x(i)j−μ(i),foralljxj(i):=xj(i)−μ(i),forallj

请注意：1）对每个输入图像块x(i)x(i)都要单独执行上面两个步骤，2）这里的 μ(i)μ(i)是指图像块 x(i)x(i) 的平均亮度值。尤其需要注意的是，这和为每个像素 xjxj单独估算均值是两个完全不同的概念。
如果你处理的图像并非自然图像（比如，手写文字，或者白背景正中摆放单独物体），其他规整化操作就值得考虑了，而哪种做法最合适也取决于具体应用场合。但对自然图像而言，对每幅图像进行上述的零均值规整化，是默认而合理的处理。

PCA白化

我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化（一些文献中也叫sphering）。举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。

如何消除输入特征之间的相关性? 在前文计算x(i)rot=UTx(i)xrot(i)=UTx(i)时实际上已经消除了输入特征x(i)x(i)之间的相关性。得到的新特征 xrotxrot的分布如下图所示：

这个数据的协方差矩阵如下：

 

[7.29000.69].[7.29000.69].

(注: 严格地讲, 这部分许多关于“协方差”的陈述仅当数据均值为0时成立。下文的论述都隐式地假定这一条件成立。不过即使数据均值不为0，下文的说法仍然成立，所以你无需担心这个。)

xrotxrot协方差矩阵对角元素的值为 λ1λ1和 λ2λ2 绝非偶然。并且非对角元素值为0; 因此, xrot,1和xrot,2xrot,1和xrot,2是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。
为了使每个输入特征具有单位方差，我们可以直接使用 1/λi−−√1/λi作为缩放因子来缩放每个特征xrot,ixrot,i。具体地，我们定义白化后的数据 xPCAwhite∈RnxPCAwhite∈ℜn如下：

 

xPCAwhite,i=xrot,iλi−−√.xPCAwhite,i=xrot,iλi.

绘制出 xPCAwhitexPCAwhite ，我们得到: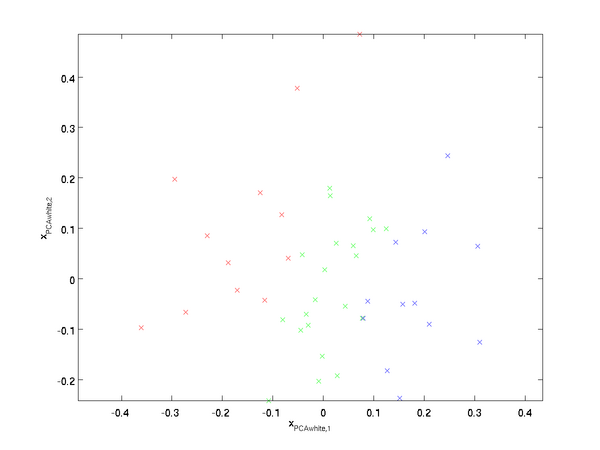

这些数据现在的协方差矩阵为单位矩阵 II。我们说，xPCAwhitexPCAwhite 是数据经过PCA白化后的版本: xPCAwhitexPCAwhite中不同的特征之间不相关并且具有单位方差。
白化与降维相结合。 如果你想要得到经过白化后的数据，并且比初始输入维数更低,可以仅保留 xPCAwhitexPCAwhite中前 kk 个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论)，xPCAwhitexPCAwhite中最后的少量成分将总是接近于0，因而舍弃这些成分不会带来很大的问题。

ZCA白化

最后要说明的是，使数据的协方差矩阵变为单位矩阵II的方式并不唯一。具体地，如果 RR 是任意正交矩阵，即满足RRT=RTR=IRRT=RTR=I(说它正交不太严格，RR 可以是旋转或反射矩阵), 那么RxPCAwhiteRxPCAwhite仍然具有单位协方差。在ZCA白化中，令 R=UR=U。我们定义ZCA白化的结果为：

 

xZCAwhite=UxPCAwhitexZCAwhite=UxPCAwhite

绘制xZCAwhitexZCAwhite，得到:

可以证明，对所有可能的 RR，这种旋转使得 xZCAwhitexZCAwhite尽可能地接近原始输入数据 xx。
当使用 ZCA白化时(不同于 PCA白化)，我们通常保留数据的全部nn 个维度，不尝试去降低它的维数。

正则化

实践中需要实现PCA白化或ZCA白化时，有时一些特征值λiλi在数值上接近于0，这样在缩放步骤时我们除以λi−−√λi将导致除以一个接近0的值；这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数 \textstyle \epsilon：

 

xPCAwhite,i=xrot,iλi+ϵ−−−−−√.xPCAwhite,i=xrot,iλi+ϵ.

当xx在区间 [−1,1][−1,1] 上时, 一般取值为 ϵ≈10−5ϵ≈10−5。
对图像来说, 这里加上ϵϵ ，对输入图像也有一些平滑(或低通滤波)的作用。这样处理还能消除在图像的像素信息获取过程中产生的噪声，改善学习到的特征(细节超出了本文的范围)。

ZCA 白化是一种数据预处理方法，它将数据从 xx映射到 xZCAwhitexZCAwhite。 事实证明这也是一种生物眼睛(视网膜)处理图像的粗糙模型。具体而言，当你的眼睛感知图像时，由于一幅图像中相邻的部分在亮度上十分相关，大多数临近的“像素”在眼中被感知为相近的值。因此，如果人眼需要分别传输每个像素值（通过视觉神经）到大脑中，会非常不划算。取而代之的是，视网膜进行一个与ZCA中相似的去相关操作 (这是由视网膜上的ON-型和OFF-型光感受器细胞将光信号转变为神经信号完成的)。由此得到对输入图像的更低冗余的表示，并将它传输到大脑。

PCA与白化_pca白化-CSDN博客

转载自：https://my.oschina.net/findbill/blog/543485

为什么80%的码农都做不了架构师？>>>   

教程地址：斯坦福深度学习

白化

什么是白化？

维基百科给出的描述是：

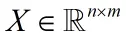
即对数据做白化处理必须满足两个条件：

1. 使数据的不同维度去相关；

2. 使数据每个维度的方差为1；

条件1要求数据的协方差矩阵是个对角阵；条件2要求数据的协方差矩阵是个单位矩阵。

为什么使用白化？

教程给出的解释是：

假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性。

比如在独立成分分析（ICA）中，对数据做白化预处理可以去除各观测信号之间的相关性，从而简化了后续独立分量的提取过程，而且，通常情况下，数据进行白化处理与不对数据进行白化处理相比，算法的收敛性较好。

 

PCA白化 与 ZCA白化

PCA 白化

我曾在 这篇 文章里详细介绍了 PCA 的原理。

给定训练数据集（假设每个特征都具有零均值）：

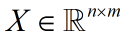
n 是数据维度；m 是样本个数。

数据的协方差矩阵为：

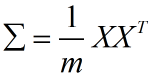
对协方差矩阵做奇异值分解：

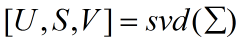
U 是 Σ 的特征向量矩阵，S 是其特征值矩阵；因为 Σ 是对称方阵，所以 V=U'，Σ=USV。

PCA 白化的定义如下：

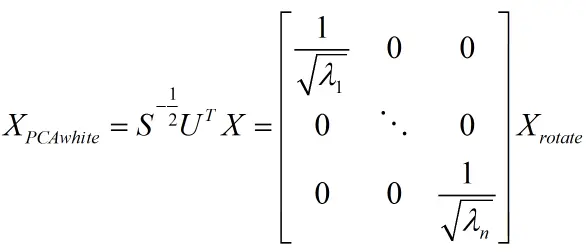
其中，Xrotate 就是原数据在主成分轴上的投影，而 S^(-1/2) 相当于对每一个主轴上的数据做一个缩放，缩放因子就是除以对应特征值的平方根。

所以：

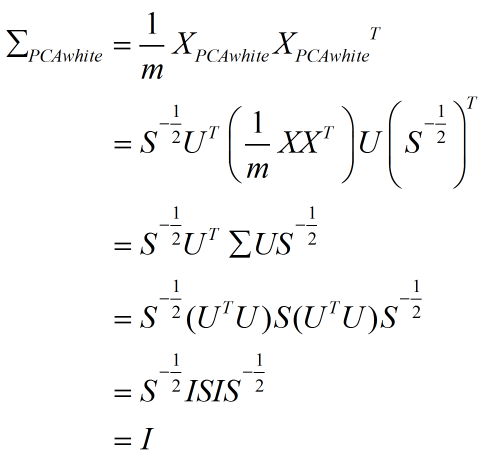
上式第 2 步是把 XPCAwhite 表达式带入得到的；第 3 步利用了矩阵 S 是对角阵的特性；第 4 步是将 Σ 作奇异值分解得到的；第 5 步利用了 U 是酉矩阵的性质（U'U=UU'=I）。

可见数据在经过 PCA 白化以后，其协方差矩阵是一个单位矩阵，即各维度变得不相关，且每个维度方差都是 1。

ZCA 白化

教程里给 ZCA 白化的定义是：

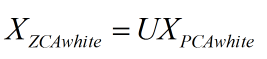
相当于将经过 PCA 白化后的数据重新变换回原来的空间。

所以：

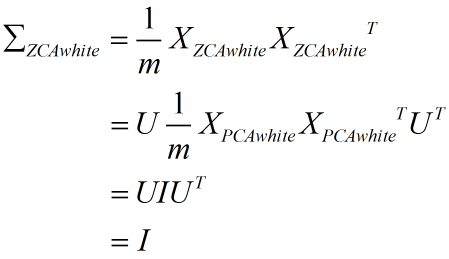
可见 ZCA 白化也是一个合法的白化。

PCA 白化 与 ZCA 白化

如何理解两者之间的关系？

首先，PCA 白化将原数据变换（投影）到主成分轴上，这一步消除了特征之间的相关性；

其次，PCA 白化对每一个主成分轴上的数据进行缩放，使其方差为 1；

因为以上的线性变换是在主成分空间中完成的，为了使白化后的数据尽可能接近原数据，可以把处理过的数据再变换回原空间，也就是 ZCA 白化。

ZCA 白化的全称是 Zero-phase Component Analysis Whitening。我对【零相位】的理解就是，相对于原来的空间（坐标系），白化后的数据并没有发生旋转（坐标变换）。

放一张来自网络的图片帮助读者直观理解：

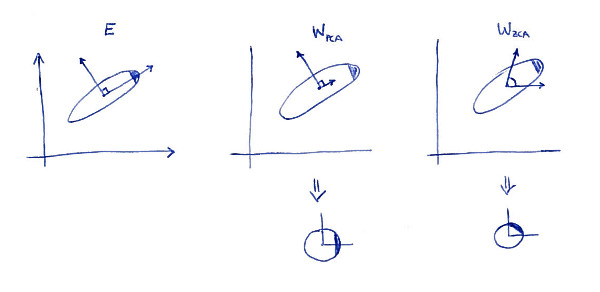
*图片来自 这里

正则化

在实践中，PCA 与 ZCA 白化都需要被正则化（Regularization）。即在缩放这个步骤之前，给每一个特征值先加上一个正则化项：

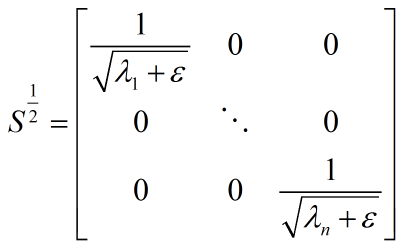
教程给出的原因有两个：

1. 有时一些特征值在数值上接近0，在缩放步骤时将导致除以一个接近0的值；这可能使数据上溢或造成数值不稳定；

2. 对图像来说，正则化项对输入图像也有一些平滑去噪（或低通滤波）的作用，可改善学习到的特征。

以 PCA 白化为例，经过正则化的数据协方差矩阵为：

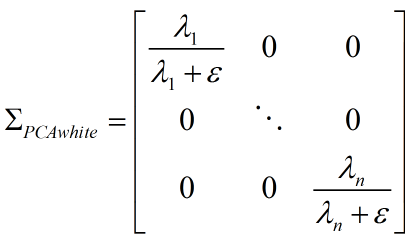
相当于减小了每个像素的不确定性（方差）。

关于低通滤波，可以这样理解：

最简单的低通滤波就是把一个像素的色值替换为其周围像素色值的算术平均。可以想象，经过处理之后的图像色彩变化更平缓，图像变得更模糊。

为什么要这样做？首先，数字图像总是伴随着噪点。其次，噪点总是伴随着色值的剧烈变化，因为每个噪点都是独立产生的。但是原图像的像素之间并不是独立的，表现为多像素构成的“色块”。

低通滤波器对“剧烈的"、"高频的”变化更敏感，所以它对噪音的影响大于对原图像的影响。经过低通滤波处理的图像可以展示出原本被噪音掩盖的细节。

这篇文章 对低通滤波的解释很直观。

 

课后练习

这次提交了 3 组代码：

pca_2d 和 pca_exercise 是教程的作业；pca_vs_zca 是我编写的用来对二者作比较的代码。

代码不复杂，所以这里直接给出 pca_vs_zca  的运行结果：

图1：原始数据

 

图2：零均值化以后的数据

图3：PCA 白化所使用的基

图4：ZCA 白化所使用的基：

本例使用的图片尺寸均为 12×12，数据具有 144 个维度，可以认为ZCA 白化的每一个基都处于其中一个维度（一个像素），即 ZCA 白化针对原数据每一个维度分别提取特征，而 PCA 白化是针对进行主成分变换后的数据的每一个维度提取特征，前者是高度局部化的，后者着眼于全局。

图5：PCA 白化后的数据

图6：ZCA 白化后的数据：

显然 ZCA 白化相比 PCA 白化更接近原数据。

 

                                    </div>
                                        </div>

 

 

低通滤波（模糊）

最基本的滤波操作称为“低通”。低通滤波器，也称为“模糊”或“平滑”滤波器，可以平均化强度的快速变化。最简单的低通滤波器只是计算一个像素及其所有八个相邻像素的平均值。结果将替换该像素的原始值。该过程对图像中的每个像素重复进行。

 

低通滤波器前后

这张低通滤波后的图像看起来模糊了很多。但为什么你想要一张更模糊的图像呢？图像通常都会有噪点——无论相机有多好，它总会在图像中添加一些“雪花”。光本身的统计特性也会给图像带来噪点。

由于每个像素都会产生独立的噪声，因此噪声总是会从一个像素快速变化到另一个像素。望远镜拍摄的图像并非如此“不相关”，因为真实图像分布在许多像素上。因此，低通滤波器对噪声的影响大于对图像的影响。通过抑制噪声，可以看到之前不可见的渐进变化。因此，低通滤波器有时可以用来呈现被噪声掩盖的微弱细节。

MaxIm DL允许您选择性地将低通滤波器应用于图像中的特定亮度范围。这允许您选择性地平滑图像背景，同时保持明亮区域不变。这是一个很好的折衷方案，因为背景中较暗的物体噪声最大，并且它不会降低明亮前景物体的清晰度。

可以通过绘制“卷积核”来直观地展示滤波过程。卷积核是一个小网格，用于显示像素的滤波值如何依赖于其相邻像素。为了通过简单地平均相邻像素来执行低通滤波，可以使用以下卷积核：

 

+1/9	+1/9	+1/9
+1/9	+1/9	+1/9
+1/9	+1/9	+1/9

 

应用此核时，每个像素及其八个相邻像素乘以 1/9 并相加。中间的像素将被替换为和。对图像中的每个像素重复此操作。

如果我们不想过滤得那么严厉，我们可以改变内核来减少平均值，例如：

 

0	+1/8	0
+1/8	+1/2	+1/8
0	+1/8	0

 

中心像素贡献其一半的值，中心上下左右四个像素各贡献其八分之一的值。这将产生更微妙的效果。通过选择不同的低通滤波器，我们可以找到一个具有足够噪声平滑度，同时又不会使图像过于模糊的滤波器。

我们也可以把核做得更大。上面的示例是 3x3 像素，总共 9 个。我们可以轻松地使用 5x5 甚至更大的核。使用更大核的唯一问题是所需的计算量会变得非常大。

此技术的一个变体是高斯模糊，它允许你仅用一个数字——高斯（“正态”）分布的半径——来定义特定形状的模糊内核。这可以非常精细地控制模糊量；半径越大，效果越强。

Py之imblearn：imblearn/imbalanced-learn库的简介、安装、使用方法之详细攻略-CSDN博客

Py之imblearn：imblearn/imbalanced-learn库的简介、安装、使用方法之详细攻略

 

目录

imblearn/imbalanced-learn库的简介

imblearn/imbalanced-learn库的安装

imblearn/imbalanced-learn库的使用方法

1、用法详解

---

 

 

 

imblearn/imbalanced-learn库的简介

        imblearn/imbalanced-learn是一个python包，它提供了许多重采样技术，常用于显示强烈类间不平衡的数据集中。它与scikit learn兼容，是 scikit-learn-contrib 项目的一部分。Imbalanced-learn 是一个 Python 库，专门用于处理不平衡数据集的机器学习问题。该库提供了一系列的重采样技术、组合方法和机器学习算法，旨在提高在不平衡数据集上的分类性能。它支持欠采样、过采样、结合欠采样和过采样的方法，以及一些集成学习方法。
        Imbalanced-learn 的主要特点包括：

• >>多样性：Imbalanced-learn 提供了多种不同的重采样技术，包括基于欠采样和过采样的方法，以及结合欠采样和过采样的方法。此外，它还提供了一些组合方法，如集成学习和自适应集成学习等，以便于用户选择合适的方法。
• >>可扩展性：Imbalanced-learn 支持与 Scikit-learn 和 Pandas 等常见的 Python 库的集成，可以方便地与其他的机器学习算法和工具进行组合和使用。
• >>灵活性：Imbalanced-learn 提供了多种参数调整和定制化的选项，以便于用户根据不同的应用场景和需求进行调整和定制化。

在python3.6+下测试了imbalanced-learn。依赖性要求基于上一个scikit学习版本：

• scipy(>=0.19.1)
• numpy(>=1.13.3)
• scikit-learn(>=0.22)
• joblib(>=0.11)
• keras 2 (optional)
• tensorflow (optional)

GitHub链接：https://github.com/scikit-learn-contrib/imbalanced-learn

 

 

 

 

imblearn/imbalanced-learn库的安装

1. pip install imblearn
2.  
3. pip install imbalanced-learn
4. pip install -i https://mirrors.aliyun.com/pypi/simple imbalanced-learn
5. pip install -U imbalanced-learn
6. conda install -c conda-forge imbalanced-learn

AI写代码

 

 

imblearn/imbalanced-learn库的使用方法

1、用法详解

         大多数分类算法只有在每个类的样本数量大致相同的情况下才能达到最优。高度倾斜的数据集，其中少数被一个或多个类大大超过，已经证明是一个挑战，但同时变得越来越普遍。解决这个问题的一种方法是通过重新采样数据集来抵消这种不平衡，希望得到一个比其他方法更健壮和公平的决策边界。

Re-sampling techniques are divided in two categories:

1. Under-sampling the majority class(es).
2. Over-sampling the minority class.
3. Combining over- and under-sampling.
4. Create ensemble balanced sets.

Below is a list of the methods currently implemented in this module.

• Under-sampling

  1. Random majority under-sampling with replacement
  2. Extraction of majority-minority Tomek links [1]
  3. Under-sampling with Cluster Centroids
  4. NearMiss-(1 & 2 & 3) [2]
  5. Condensed Nearest Neighbour [3]
  6. One-Sided Selection [4]
  7. Neighboorhood Cleaning Rule [5]
  8. Edited Nearest Neighbours [6]
  9. Instance Hardness Threshold [7]
  10. Repeated Edited Nearest Neighbours [14]
  11. AllKNN [14]

• Over-sampling

  1. Random minority over-sampling with replacement
  2. SMOTE - Synthetic Minority Over-sampling Technique [8]
  3. SMOTENC - SMOTE for Nominal Continuous [8]
  4. bSMOTE(1 & 2) - Borderline SMOTE of types 1 and 2 [9]
  5. SVM SMOTE - Support Vectors SMOTE [10]
  6. ADASYN - Adaptive synthetic sampling approach for imbalanced learning [15]
  7. KMeans-SMOTE [17]

• Over-sampling followed by under-sampling

  1. SMOTE + Tomek links [12]
  2. SMOTE + ENN [11]

• Ensemble classifier using samplers internally

  1. Easy Ensemble classifier [13]
  2. Balanced Random Forest [16]
  3. Balanced Bagging
  4. RUSBoost [18]
• Mini-batch resampling for Keras and Tensorflow