召回率精确率 matlab,「机器学习」准确率、精确率、召回率、F1分数、ROC-AUC

机器学习

在机器学习中衡量一个模型是否准确我们有很多指标：

准确率 - accuracy

精确率 - precision

召回率 - recall

F1分数-F1 score

ROC曲线下面积 - ROC-AUC (area under curve)

那么，这些指标到底都是什么呢？各自有什么优缺点呢？笔者在了解这些指标的时候是在网上各大网站(CSDN、博客园、知乎)上找文章学习的。但是这些文章要么是过于数学化，要么是有地方不那么好读(前后变量不一致导致阅读苦难)、要么是过于“去数学化”。我自己整理了一份学习笔记，一定能够让大家一次性读懂这几个指标。

下面进入正文：

大家要明白，以上指标统统离不开一个工具：混淆矩阵-confusion matrix

混淆矩阵是个什么东西？

对于二分类问题，每一条数据要么预测正确，表示为1；要么预测错误，表示为0(注意这里是预测结果正确与否，而不是预测结果是0还是1)，而事物本身也是被分为0(负样本)和1(正样本)两类。

用矩阵来表示就是这个样子

![混淆矩阵](https://dataset.flyai.com/混淆矩阵.jpg)

TP：True&Positive(positive表示正样本，true表示预测正确，即预测为positive是正确的)

FP：False&Positive(positive表示正样本，false表示预测错误，即预测为positive是错误的)

FN：False&Negative(negative表示负样本，false表示预测错误，即预测为negative是错误的)

TN：True&Negative(negative表示负样本，true表示预测正确，即预测为negative是正确的)

下面正式讲解五种指标：

**一、准确率**

很直观，就是预测正确的个数/总样本数，如果用混淆矩阵里的数据表示，就是(TP+TN)/(TP+FP+FN+TN)。讲道理这其实是正常人最能理解也最常用的评价指标了。但其实这个指标有个缺陷。机器学习的模型经常会出现在一个数据集上表现良好，但是在另一个数据集上却一塌糊涂的情况。假设一个数据集有100条数据，99个1，1个0，而你的模型所有的输出都是1，那么你的模型在该数据集上的准确率是99%，惊人的高。但实际上你的模型没有意义，因为只能输出1。这就反映出了准确率的弊端。

![准确率](https://dataset.flyai.com/准确率.jpeg)

**二、精确率**

又名查准率，类似于准确率，但有别于准确率。精确率指的是预测为1的样本中实际为1的频率，也就是TP/(TP+FP)。精确率代表的是正样本结果中的预测准确度，准确率是既考虑了正样本也考虑了负样本。照这个逻辑，上面的例子的精确率是0.99。

![精准率](https://dataset.flyai.com/精确率.jpeg "精准率")

**三、召回率**

召回率又叫查全率，其公式为TP/(TP+FN)。这个比率反映了正样本被正确预测的比例，在传染病学领域有极高的意义，我们规定“有病”为正样本，即为1。TP表示被在正确诊断为有病的个数，FN表示本来有病却被诊断为没病的个数。召回率越高，表示我们准确确诊的能力就越强。召回率低说明有大量有病案例被诊断为没病，这就非常可怕。

![召回率](https://dataset.flyai.com/召回率.jpeg "召回率")

**四、F1分数**

F1分数的计算公式为：

F1score=(2*precision*recall)/(precision+recall)

如果将F1分数在不同阈值(阈值的概念下面有介绍)下绘制出来，就得到了P-R曲线(精确率-召回率曲线)。何为阈值？我们都知道，对于二分类问题，模型的输出仅仅是概率，当1的概率为0.8，0的概率为0.2时，我们认为模型预测的结果为1。一般情况下，我们取大于0.5的那个概率作为模型的预测结果，这个0.5就是阈值。但是实际中，阈值为0.5的时候可能不能保证模型的精确率和召回率，因此，我们常常需要尝试不用的阈值，该曲线就是在不同阈值下绘制的P-R关系图。

**F1分数其实是精确率和召回率的调和平均(倒数之和的平均值的倒数)**

**五、ROC_AUC**

ROC(receiver operating characteristic curve：接受者操作特征曲线)是一条曲线。该曲线涉及两个指标：真正率(TPR)和假正率(FPR)

真正率就是召回率，假正率(1-特异度)=FP/(FP+TN)。

![真正率和假正率](https://dataset.flyai.com/真假正率.jpeg "真正率和假正率")

上面是真正率和假正率的示意，我们发现**TPR 和 FPR 分别是基于实际表现 1 和 0 出发的(注意看分母，分母分别是实际为1和实际为0)，也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。 **正因为如此，所以无论样本是否平衡，都不会被影响。还是拿之前的例子，总样本中，99% 是正样本，1% 是负样本。我们知道用准确率是有水分的，但是用 TPR 和 FPR 不一样。这里，TPR 只关注 99% 正样本中有多少是被真正覆盖的，而与那 1% 毫无关系，同理，FPR 只关注 1% 负样本中有多少是被错误覆盖的，也与那 99% 毫无关系。通俗的讲：**真正率就是正样本中预测正确的比率，假正率就是负样本中预测错误的比率。**按照这个逻辑，上面的例子中真正率为1，假正率为1。

我们以FPR为x轴，TPR为y轴画图，就得到了ROC曲线。

与F1分数曲线一样的是，ROC也是通过遍历阈值的方式绘制的。

![ROC曲线](https://dataset.flyai.com/roc.gif)

我们如何通过ROC曲线判断一个模型的好坏？

针对一个模型，我们希望的是假正率(X值，自变量)一定的时候真正率(Y值，因变量)越高越好，也就是曲线“越上凸”就越好。

由于，ROC曲线的xy值都是正负样本的准确率(错误率)，**因此，无论我们给的样例中正负样本的个数孰多孰少，都不会影响ROC的形状，我们可以称ROC曲线“无视样本的不平衡”，**这是ROC曲线比前几种指标更加准确合理的根本原因。

![ROC曲线无视样本的不平衡](https://dataset.flyai.com/无视不平衡.gif)

那AUC(曲线下面积)又是干嘛的呢？

上面提到，ROC曲线越上凸模型就越好，那有没有什么度量指标能够量化这种好呢？答案就是用曲线下方的面积，也就是曲线在0到1上的积分。

比较有意思的是，如果我们连接对角线，它的面积正好是 0.5。**对角线的实际含义是：随机判断响应与不响应，正负样本覆盖率应该都是 50%，表示随机效果。** ROC 曲线越陡越好，所以理想值就是 1，一个正方形，而最差的随机判断都有 0.5，所以一般 AUC 的值是介于 0.5 到 1 之间的。

机器学习-理解Accuracy，Precision，Recall, F1 score以及sklearn实现 - 知乎

在机器学习的分类任务中，绕不开准确率(accuracy)，精确率(precision)，召回率(recall)，PR曲线，F1 score这几个评估分类效果的指标。而理解这几个评价指标各自的含义和作用对全面认识分类模型的效果有着重要的作用。

本文将对这几个评价指标进行讲解，并结合sklearn库进行代码实现。

混淆矩阵

在介绍分类任务各个指标之前，需要先了解混淆矩阵（Confusion Matrix）的概念，因为混淆矩阵可以使后续计算准确率，精确率，召回率思路更加清晰。混淆矩阵如下图所示：

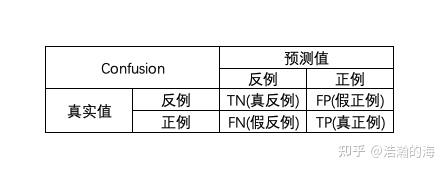
真正例和真反例是被正确预测的数据，假正例和假反例是被错误预测的数据。接下来的内容基本都是围绕这个四个值展开，所以需要理解这四个值的具体含义：

TP（True Positive）：被正确预测的正例。即该数据的真实值为正例，预测值也为正例的情况；
TN（True Negative）：被正确预测的反例。即该数据的真实值为反例，预测值也为反例的情况;
FP（False Positive）：被错误预测的正例。即该数据的真实值为反例，但被错误预测成了正例的情况；
FN（False Negative）：被错误预测的反例。即该数据的真实值为正例，但被错误预测成了反例的情况。

当理解上面四个值之后，接下来将介绍Accuracy, Precision, Recall，F1 score。

准确率

准确率（Accuracy）表示分类正确的样本占总样本个数的比例。

分类正确的样本有两部分组成，分别是预测为正且真实为正的情况，即TP；还有是预测为负且真实也为负的情况，即TN。

总样本个数即为TP, FP, TN, FN之和。

故计算公式如下：

$A c c u r a c y = \frac{T P + T N}{T P + F P + T N + F N}$

Accuracy是衡量分类模型的最直白的指标，但缺陷也是明显的。假设有100个样本，其中有99个都是正样本，则分类器只需要一直预测为正例，就可以得到99%的准确率，实际上这个分类器性能是很低下的。也就是说，当不同类别的样本所占的比例严重不平衡时，占比大的类别会是影响准确率的最主要的因素。所以，只有当数据集各个类别的样本比例比较均衡时，Accuracy这个指标才是一个比较好的衡量标准。因此，必须参考其他指标才能完整评估模型的性能。

下面来看下sklearn中计算accuracy的示例：

import numpy as np
from sklearn.metrics import accuracy_score

y_pred = [2, 1, 1, 0]
y_true = [0, 1, 2, 3]
print(accuracy_score(y_true, y_pred)) # 0.25
print(accuracy_score(y_true, y_pred, normalize=False)) # 1

# 在具有二元标签指示符的多标签分类案例中
print(accuracy_score(np.array([[0,1], [1,1]]), np.ones((2, 2)))) # 0.5

函数接口的描述：

准确度分类得分
在多标签分类中，此函数计算子集精度：为样本预测的标签集必须完全匹配y_true（实际标签）中相应的标签集。
参数
y_true: 一维数组，或标签指示符 / 稀疏矩阵，实际（正确的）标签.
y_pred: 一维数组，或标签指示符 / 稀疏矩阵，分类器返回的预测标签.
normalize: 布尔值, 可选的(默认为True). 如果为False，返回分类正确的样本数量，否则，返回正确分类的得分.
sample_weight: 形状为[样本数量]的数组，可选. 样本权重.
返回值
score: 浮点型
如果normalize为True，返回正确分类的得分（浮点型），否则返回分类正确的样本数量（整型）.
当normalize为True时，最好的表现是score为1，当normalize为False时，最好的表现是score未样本数量.

精确率

精确率（Precision）又叫查准率，表示预测结果为正例的样本中实际为正样本的比例。

计算公式为：

$P r e c i s i o n = \frac{T P}{T P + F P}$

使用场景：当反例被错误预测成正例（FP）的代价很高时，适合用精确率。根据公式可知，精确率越高，FP越小。比如在垃圾在垃圾邮件检测中，假正例意味着非垃圾邮件（实际为负）被错误的预测为垃圾邮件（预测为正）。如果一个垃圾邮件监测系统的查准率不高导致很多非垃圾邮件被归到垃圾邮箱里去，那么邮箱用户可能会丢失或者漏看一些很重要的邮件。

下面来看下sklearn中计算precision的示例：

from skearn.metrics import precision_score

y_pred = [0, 2, 1, 0, 0 ,1]
y_true = [0, 1 ,2, 0 ,1, 2]

print(precision_score(y_true, y_pred, average='micro')) # 0.3333333333333333
print(precision_score(y_true, y_pred, average='macro')) # 0.2222222222222222
print(precision_score(y_true, y_pred, average='weighted')) # 0.2222222222222222
print(precision_score(y_true, y_pred, average=None)) # [0.66666667 0.         0.        ]

函数接口的描述：

计算精确率
精确率是 tp / (tp + fp)的比例，其中tp是真正性的数量，fp是假正性的数量. 精确率直观地可以说是分类器不将负样本标记为正样本的能力.
精确率最好的值是1，最差的值是0.
参数
y_true: 一维数组，或标签指示符 / 稀疏矩阵，实际（正确的）标签.
y_pred: 一维数组，或标签指示符 / 稀疏矩阵，分类器返回的预测标签.
labels : 列表，可选值. 当average != binary时被包含的标签集合，如果average是None的话还包含它们的顺序. 在数据中存在的标签可以被排除，比如计算一个忽略多数负类的多类平均值时，数据中没有出现的标签会导致宏平均值（marco average）含有0个组件. 对于多标签的目标，标签是列索引. 默认情况下，y_true和y_pred中的所有标签按照排序后的顺序使用.
pos_label : 字符串或整型，默认为1. 如果average = binary并且数据是二进制时需要被报告的类. 若果数据是多类的或者多标签的，这将被忽略；设置labels=[pos_label]和average != binary就只会报告设置的特定标签的分数.
average : 字符串，可选值为[None, ‘binary’ (默认), ‘micro’, ‘macro’, ‘samples’, ‘weighted’]. 多类或者多标签目标需要这个参数. 如果为None，每个类别的分数将会返回. 否则，它决定了数据的平均值类型.
‘binary’: 仅报告由pos_label指定的类的结果. 这仅适用于目标（y_{true, pred}）是二进制的情况.
‘micro’: 通过计算总的真正性、假负性和假正性来全局计算指标.
‘macro’: 为每个标签计算指标，找到它们未加权的均值. 它不考虑标签数量不平衡的情况.
‘weighted’: 为每个标签计算指标，并通过各类占比找到它们的加权均值（每个标签的正例数）.它解决了’macro’的标签不平衡问题；它可以产生不在精确率和召回率之间的F-score.
‘samples’: 为每个实例计算指标，找到它们的均值（只在多标签分类的时候有意义，并且和函数accuracy_score不同）.
sample_weight : 形状为[样本数量]的数组，可选参数. 样本权重.
返回值
precision: 浮点数(如果average不是None) 或浮点数数组, shape =[唯一标签的数量]
二分类中正类的精确率或者在多分类任务中每个类的精确率的加权平均.

为了更加直白的讲解sklearn中precision的多个计算方式，现介绍下两个与多分类相关的概念，然后讲上面的代码是如何计算的。

Macro average

宏平均是指在计算均值时使每个类别具有相同的权重，最后结果是每个类别的指标的算术平均值。

Micro average

微平均是指计算多分类指标时赋予所有类别的每个样本相同的权重，将所有样本合在一起计算各个指标。

由precision_score的接口文档可知，当average=None时，得到的结果是是每个类别的precision。上面的y_true有三个类别，分别是0， 1， 2。每个类别的TP, FP, FN如下表所示：

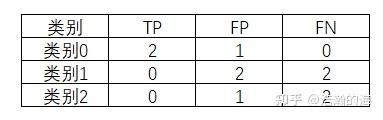
那么，可以得到每个类别的精确率了。

$P_{0} = \frac{2}{1 + 2} \approx 0.667$

$P_{1} = \frac{0}{0 + 2} = 0$

$P_{2} = \frac{0}{0 + 1} = 0$

则Macro average也可以得出，为 $(P_{0} + P_{1} + P_{2}) / 3 \approx 0.222$

Micro average的计算需要从每个样本考虑，所有样本中预测正确的有两个，则TP为2，剩下的4个预测结果都可以看成FP，则Micro Precision等于 $2 / (2 + 4) \approx 0.333$

average='weighted'考虑的是每一类与所有样本的占比，然后求加权平均值。因为这里每类的样本数都是2，与总体样本的占比都是1/3，故average='weighted'的精确率为

$P_{w} = \frac{1}{3} * P_{0} + \frac{1}{3} * P_{1} + \frac{1}{3} * P_{2} \approx 0.222$

对比下Macro和Micro：

如果每个类别的样本数量差不多，那么宏平均和微平均没有太大差异
如果每个类别的样本数量差异很大，那么注重样本量多的类时使用微平均，注重样本量少的类时使用宏平均
如果微平均大大低于宏平均，那么检查样本量多的类来确定指标表现差的原因
如果宏平均大大低于微平均，那么检查样本量少的类来确定指标表现差的原因

召回率

召回率（Recall）又被称为查全率，表示预测结果为正样本中实际正样本数量占全样本中正样本的比例。

计算公式为：

$R e c a l l = \frac{T P}{T P + F N}$

使用场景：当正例被错误的预测为反例（FN）产生的代价很高时，适合用召回率。根据公式可知，召回率越高，FN越小。比如说在银行的欺诈检测或医院的病患者检测中，如果将欺诈性交易（实际为正）预测为非欺诈性交易（预测为负），则可能会给银行带来非常严重的损失。再比如以最近的新冠疫情为例，如果一个患病者（实际为正）经过试剂检测被预测为没有患病（预测为负），这样的假反例或者说假阴性产生的风险就非常大。

sklearn中recall_score方法和precision_score方法的参数说明都是一样的。所以这里不再重复，只是把函数和返回值说明贴在下面：

计算召回率
召回率是比率tp / (tp + fn)，其中tp是真正性的数量，fn是假负性的数量. 召回率直观地说是分类器找到所有正样本的能力.
召回率最好的值是1，最差的值是0.
返回值
recall: 浮点数(如果average不是None) 或者浮点数数组，shape = [唯一标签的数量]
二分类中正类的召回率或者多分类任务中每个类别召回率的加权平均值.

from sklearn.metrics import recall_score

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0 ,0, 1]
print(recall_score(y_true, y_pred, average='macro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average='weighted'))  # 0.3333333333333333
print(recall_score(y_true, y_pred, average=None))  # [1. 0. 0.]

Recall和Precision只有计算公式不同，它们average参数为’macro’，‘micro’，'weighted’和None时的计算方式都是相同的，具体计算可以使用上节列出来的TP、FP、FN表，这里不再赘述。

F1 score

F1 score是精确率和召回率的一个加权平均。

F1 score的计算公式如下：

$F_{1} = 2 * \frac{P r e c i s i o n * R e c a l l}{P r e c i s i o n + R e c a l l}$

Precision体现了模型对负样本的区分能力，Precision越高，模型对负样本的区分能力越强；Recall体现了模型对正样本的识别能力，Recall越高，模型对正样本的识别能力越强。F1 score是两者的综合，F1 score越高，说明模型越稳健。

sklearn中f1_score方法和precision_score方法、recall_score方法的参数说明都是一样的，所以这里不再重复，只是把函数和返回值说明贴在下面：

计算F1 score，它也被叫做F-score或F-measure.
F1 score可以解释为精确率和召回率的加权平均值. F1 score的最好值为1，最差值为0. 精确率和召回率对F1 score的相对贡献是相等的. F1 score的计算公式为：
F1 = 2 * (precision * recall) / (precision + recall)
在多类别或者多标签的情况下，这是权重取决于average参数的对于每个类别的F1 score的加权平均值.
返回值
f1_score : 浮点数或者是浮点数数组，shape=[唯一标签的数量]
二分类中的正类的F1 score或者是多分类任务中每个类别F1 score的加权平均.

下面来看下sklearn中计算F1的示例：

from sklearn.metrics import f1_score

y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
print(f1_score(y_true, y_pred, average='macro'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average='micro'))  # 0.3333333333333333
print(f1_score(y_true, y_pred, average='weighted'))  # 0.26666666666666666
print(f1_score(y_true, y_pred, average=None))  # [0.8 0.  0. ]

总结：当FP和FN造成的代价差不多的时候，可以直接用Accuracy。但是当FP和FN产生的代价差别很大的时候，可以考虑更好的度量方式，比如Precision, Recall和F1 score。