一个耗时4小时的内存泄漏问题&彻底理解堆
上周像往常一样例行检查线上机器性能,突然发现一个服务的内存使用率是这样的:
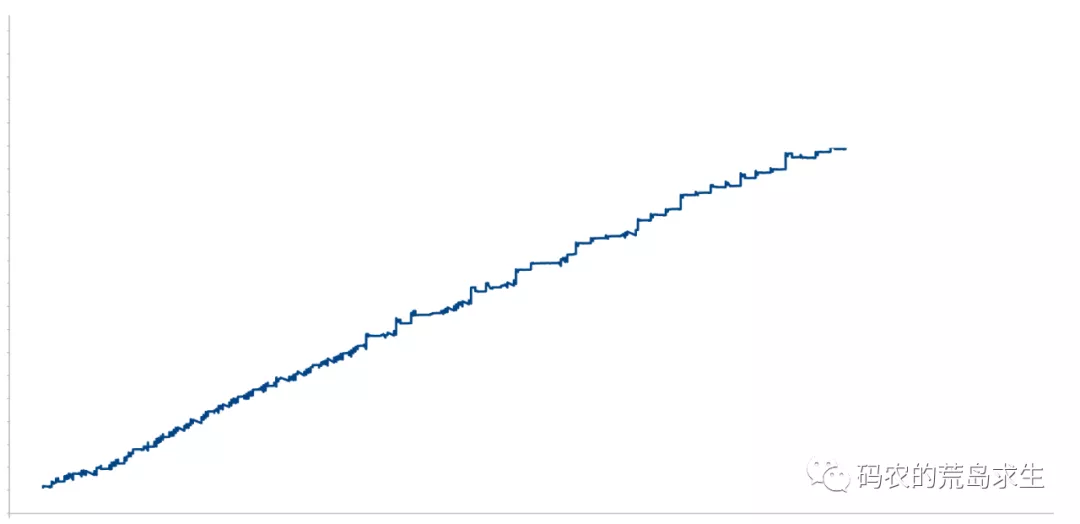
很显然该服务存在内存泄漏问题,赶紧排查问题。
问题排查
首先确定内存泄漏问题出现的时间,发现在该时间点的上线有两次代码提交,其中一个就是我的。于是立刻排查这两次代码的改动,确定了另一个同事的代码不可能会有内存问题后(因为另一个同事的上线仅仅修改了配置)我知道肯定是自己的代码出现了问题。
确定了问题所在后赶紧把自己的代码回滚掉,接下来就可以放心debug了。
Debug
什么是内存泄漏?
简单的讲就是程序员申请的内存在使用完后没有还给操作系统,由于笔者使用的是C++语言,因此内存泄漏一般是这样的:
obj* o = new obj();...// 使用完obj后没有delete掉
肯定有什么地方申请了内存后没有调用delete释放内存。
在这里介绍一下笔者的代码改动,我的任务其实是重构一段代码,把这段代码并行化。也就是旧的逻辑是在一个线程中串行执行的,现在我要把这段逻辑放到两个线程中并行执行,这是最让人头疼的任务之一,并行化改造是比较容易出bug的。
接下来梳理了一遍中所有内存的申请和释放,这其中包括:
-
使用new/delete分配释放的内存
-
使用内存池分配释放的内存
仔细梳理一遍后没有发现任何问题,该释放的内存都已经释放掉了,这时笔者已经开始怀疑人生了 :) ,很显然还有一段没有注意到的地方出现了问题,这是必然的,虽然知道问题必然出现在改动的这些代码里但是我并不能确定出现的位置。
没有办法,到这里基本上已经要放弃自己人肉debug了,想利用一些内存检测工具来帮助自己确定问题。
常见的内存泄漏检测工具包括valgrind、gperftools等,valgrind的好处在于无需重新编译代码即可进行内存检测,但是缺点是会使得程序运行非常缓慢,官方文档给的说法是会比正常的程序运行慢20-30倍;gperftools则需要重新编译可执行程序。这些工具需要下载安装测试,其中还涉及到申请机器权限等问题,笔者觉得还是比较麻烦,况且这个问题也不是大海捞针一样,问题肯定出在了并行化的这段代码中。
到这里我决定再换一个思路来排查问题,既然代码重构后开始并行执行,那么出现问题大概率是因为多线程问题,遇到多线程问题首先重点排查的就是线程间的共享数据。
多线程问题的关键——共享数据
我们知道如果线程之间没有共享数据那么就不会有线程安全问题,我们使用的锁、信号量、条件变量等其实都是用来保护共享数据的,比如锁通常是用来包括临界区的,临界区中的代码操作的就是线程共享数据;信号量使用的一个经典场景就是生产者消费者问题,生产者线程以及消费者线程都会操作同一个队列,这里的队列就是共享数据。
沿着这个思路开始找在两个线程中都使用到的共享数据,果不其然,在一个角落中发现了这样一段代码:
auto* pb = global->mutable_obj();这是分配protobuf对象的一段代码,protobuf是Google开发是一种类似于JSON、XML的技术,因此常用于网络通信和数据交换等场景,比如RPC等。
如果你不了解protobuf也没有关系,实际上上面的这段代码的要做的事情是这样的:
if (global->obj == NULL) {global->obj = new obj();}return global->obj;
值得注意的是这段代码现在会在两个线程中执行,显然问题就出现在了这里。
那么问题是怎么出现的呢?
我们假设有两个线程,线程A和线程B,当这样一段代码在线程AB中同时执行时可能会有以下场景:
-
线程A拿到global->obj并检测到此时的global->obj为空,因此决定为其分配内存,但不巧的是此时发生线程切换,线程A在为global->obj分配内存前被暂停运行,如下所示:
if (global->obj == NULL) {<------- 线程切换,线程A被暂停执行global->obj = new obj();}return global->obj;
-
线程A被暂停运行后线程B开始执行,这段代码同样会在线程B中执行一遍,因此线程B会首先检查global->obj发现为空,因此为global->obj分配内存,分配完内存后发生线程切换,线程B被暂停运行,如下所示:
if (global->obj == NULL) {global->obj = new obj();<------- 线程切换,线程B被暂停执行}return global->obj;
-
线程B被暂停运行后调度器决定重新运行线程A,此时线程A开始从被中断的地方继续运行,还记得线程A是从哪里被中断的吗,没错,就是在为global->obj分配内存前被中断的,此时线程A继续运行,也就是说global->obj = new obj()这段代码又被执行了一次,虽然线程B已经为global->obj分配了内存。
Oops,典型的内存泄漏,线程B分配的内存再也无法被正常释放掉了。
至此,我们已经找到了问题的原因,罪魁祸首就是共享数据,关键的一点是要意识到你的线程会随时被中断执行,CPU会随时切换到其它线程。
代码修复也非常简单,再新增一个变量,两个线程不在使用共享数据,到这里问题就解决了,从发现问题到完成修复耗时大概4小时。
经验教训
代码的并行化重构是一件非常棘手的任务,很容易出现线程安全问题,解决线程安全问题首先要考虑的不是要不要加锁,而是多个线程是否真的有必要使用共享数据,没有必要的话多个线程操作私有数据根本就不会出现线程安全问题。
当出现线程安全问题时,第一时间重点排查线程使用的共享数据。
内存泄漏检测工具
虽然这些没有使用检测工具全靠人肉debug其实还是因为问题排查范围比较小,如果我们根本就不知道问题出现在了那次代码改动那么检测工具就非常重要了,在这里简单介绍一下valgrind的使用,详细的介绍请参考官方文档。
假设有这样一段问题代码:
void f(void){int* x = malloc(10 * sizeof(int));x[10] = 0; // 问题1: 越界} // 问题2: 内存泄漏,x没有被释放掉int main(){f();return 0;}
这段代码中有两个问题:一个是数据的越界访问;另一个是内存泄漏。将该程序编译为myprog。
接下来使用valgrind来检查该程序,使用以下命令:
valgrind --leak-check=yes myprog运行完成后valgrind会给出检测报告,关于程序越界访问会给出这样的输出:
==19182== Invalid write of size 4==19182== at 0x804838F: f (example.c:6)==19182== by 0x80483AB: main (example.c:11)==19182== Address 0x1BA45050 is 0 bytes after a block of size 40 alloc'd==19182== at 0x1B8FF5CD: malloc (vg_replace_malloc.c:130)==19182== by 0x8048385: f (example.c:5)==19182== by 0x80483AB: main (example.c:11)
第一行告诉你代码中存在Invalid write,也就是无效的写,并给出了问题出现的位置。
关于内存泄漏问题会给出这样的输出:
==19182== 40 bytes in 1 blocks are definitely lost in loss record 1 of 1==19182== at 0x1B8FF5CD: malloc (vg_replace_malloc.c:130)==19182== by 0x8048385: f (example.c:5)==19182== by 0x80483AB: main (example.c:11)
这里第一行报告了内存"definitely lost",也就是说一定会存在内存泄漏,并给出了问题出现的位置。
实际上除了"definitely lost",valgrind还会给出"probably lost"的报告,这两种报告的含义是这样的:
-
"definitely lost":你的程序一定存在内存泄漏问题,修复。
-
"probably lost":你的程序看起来像是有内存泄漏,有可能你在使用指针完成一些特定操作,因此不一定100%存在问题。
总结
编写正确的多线程代码从来不是一件容易的事情,线程安全问题的根源在于共享资源,因此在使用共享资源前务必确认我们一定要用共享资源吗?
彻底理解堆
什么是堆
在计算机科学中堆是一种很有趣的数据结构,实际上通常用数组来存储堆中的元素,但是我们却可以把数组中元素视为树,如图所示:

这就是一个普通的数组,但是我们可以将其看做如下图所示的树:
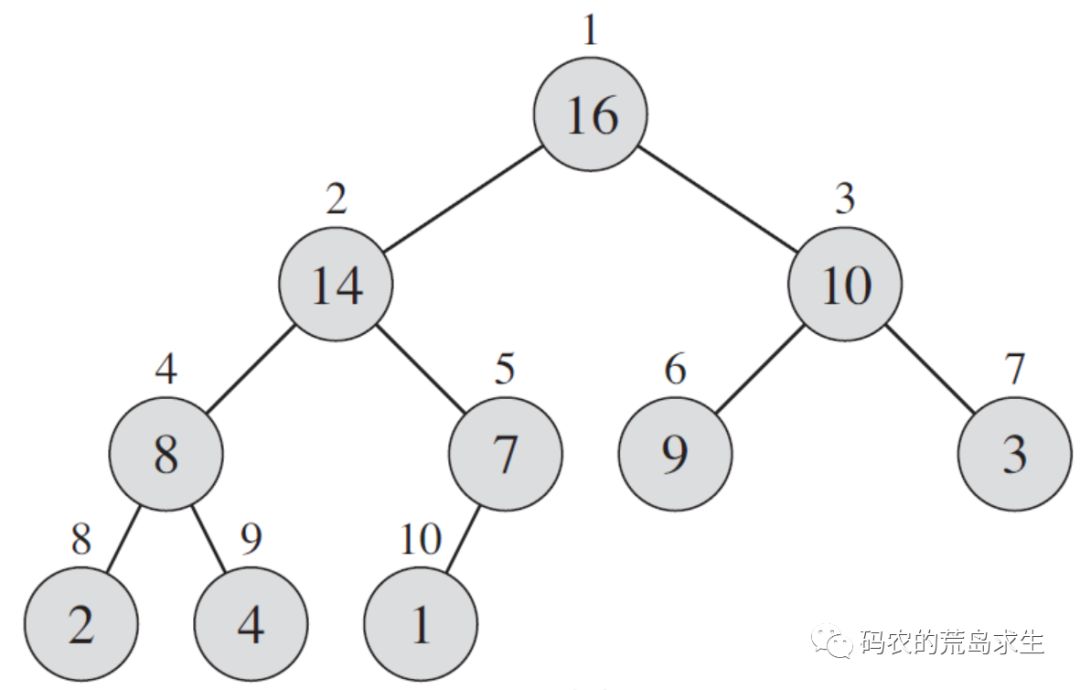
这是怎么做到的呢?
原来虽然我们是在数组中存储的堆元素,但是这里面有一条隐藏的规律,如果你仔细看上图就会发现:
-
每一个左子树节点的下标是父节点的2倍
-
每一个右子树节点的下标是父节点的2倍再加1
也就是说在数组中实际上隐藏了上面的这两条规律,如图所示:
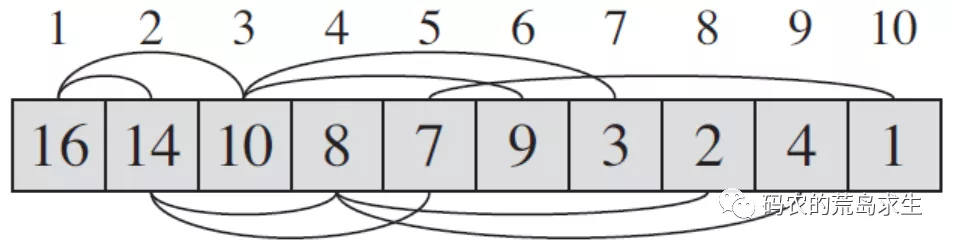
堆这种数据结构最棒的地方在于我们无需像树一样存储左右子树的信息,而只需要通过下标运算就可以轻松的找到一个节点的左子树节点、右子树节点以及父节点,如下所示,相对于树这种数据结构来说堆更加节省内存。
int parent(int i){ // 计算给定下标的父节点return i/2;}int left(int i){ // 计算给定下标的左子树节点return 2*i;}int right(int i){ // 计算给定下标的右子树节点return 2*i+1;}
除了上述数组下标上的规律以外,你还会发现堆中的每一个节点的值都比左右子树节点大,这被称为大根堆,即对于大根堆来说以下一定成立:
array[i] > array[left(i)] && array[i] > array[right(i)] == true相应的如果堆中每个一节点的值都比左右子树节点的值小,那么这被称为小根堆,即对于小根堆来说以下一定成立:
array[i] < array[left(i)] && array[i] < array[right(i)] == true以上就是堆这种数据结构的全部内容了。
那么接下来的问题就是,给定一个数组,我们该如何将数组中的值调整成一个堆呢?
如何在给定数组上创建堆
在这里我们以大根堆为例来讲解如何在给定数组上创建一个堆。
给定数组的初始状态如下图a所示,从图中我们看到除array[2]之外其它所有节点都满足大根堆的要求了,接下来我们要做的就是把array[2]也调整成为大根堆,那么该怎么调整呢?
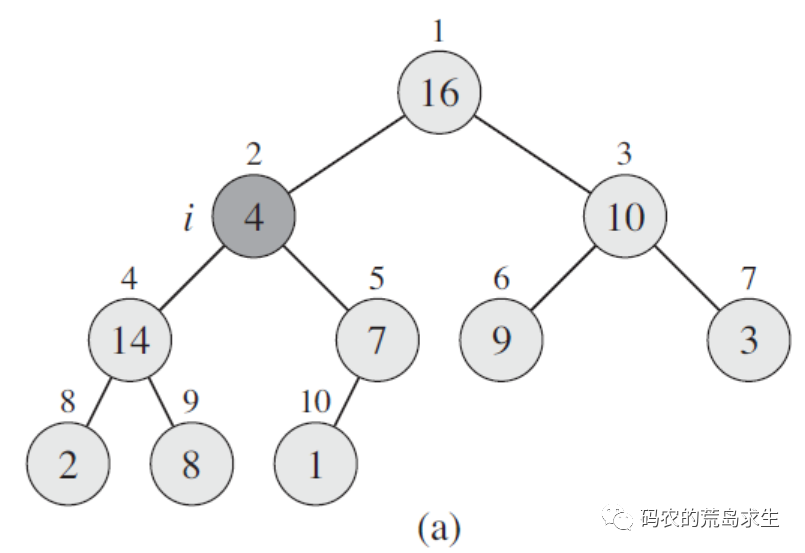
很简单,我们只需要将array[2]和其左右子树节点进行比较,最大的那个和array[2]进行交换,如上图b所示,array[2]和其左子树array[4]以及右子树array[5]中最大的是array[4],这样array[2]和array[4]进行交换,这样array[2]就满足大根堆的要求了,如图b所示;
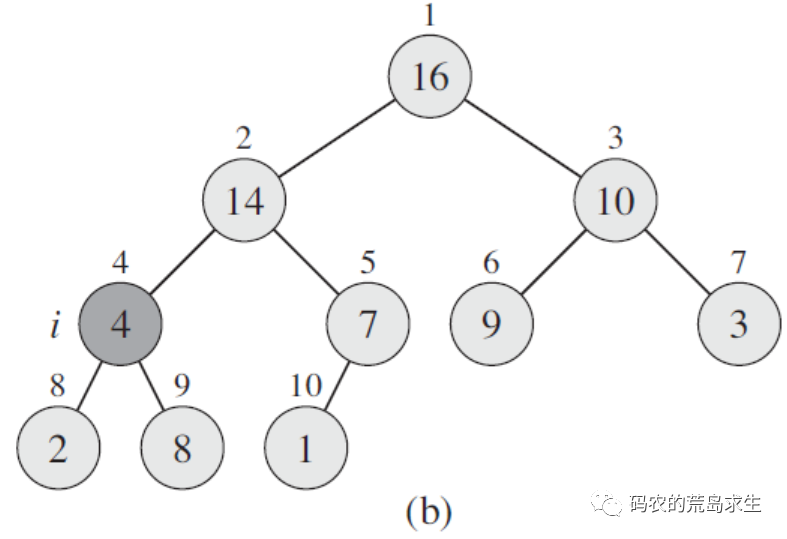
但此时array[4]不满足要求,怎么办呢?还是重复上面的过程,在array[4]的左子树和右子树中选出一个最大的和array[4]交换,最终我们来到了图c,此时所有元素都满足了堆的要求,这个过程就好比石子在水中下沉,一些资料中将这个过程称形象的称为“shift down”。
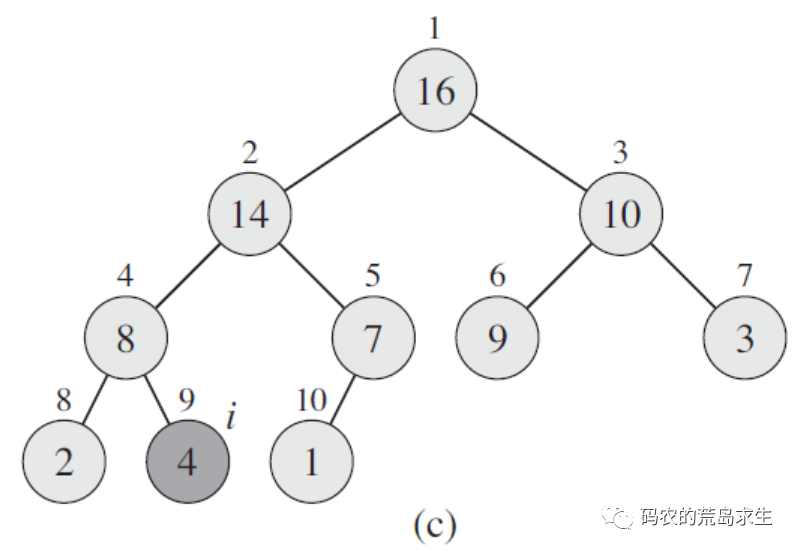
现在我们知道了假设堆中有一个元素i不满足大根堆的要求,那么该如何调整呢:
void keep_max_heap(int i){int l = left(i);int r = right(i);int larget = i;if (l < heap_size && array[l] > array[i])larget = l;if (r < heap_size && array[r] > array[larget])larget = r;if (larget != i){swap(array[larget], array[i]);max_heap(larget);}}
以上代码即keep_max_heap函数就是刚才讲解调整节点的过程,该过程的时间复杂度为O(logn)。
但是到目前为止我们依然不知道该如何在给定的数组上创建堆,不要着急,我们首先来观察一下给定的数组的初始状态,如图所示:
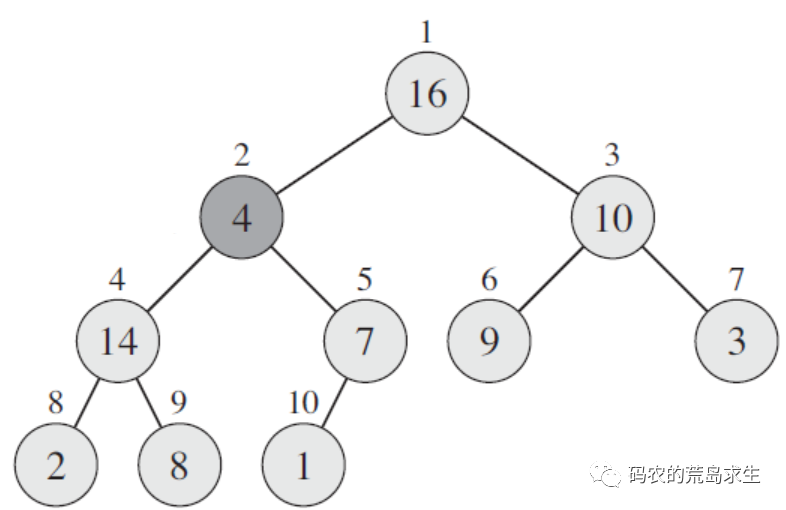
实际上堆是一颗完全二叉树,那么这对于我们来说有什么用呢?这个性质非常有用,这个性质告诉我们要想将一个数组转换为堆,我们只需要从第一个非叶子节点开始调整即可。
那么第一个非叶子节点在哪里呢?假设堆的大小为heap_size,那么第一个非叶子节点就是:
heap_size / 2;
可这是为什么呢?原因很简单,因为第一个非叶子节点总是最后一个节点的父节点,因此第一个非叶子节点就是:
parent(heap_size) == heap_size / 2
有了这些准备知识就可以将数组转为堆了,我们只需要依次在第一个非叶子节点到第二个节点上调用一下keep_max_heap就可以了:
void build_max_heap() {for (int i = heap_size/2; i>=1; i--)keep_max_heap(i);}
这样,一个堆就建成了。
增加堆节点以及删除堆节点
对于堆这种数据结构来说除了在给定数组上创建出一个堆之外,还需要支持增加节点以及删除节点的操作,在这里我们依然以大根堆为例来讲解,首先来看删除堆节点。
删除节点
删除堆中的一个节点实际用到的正是keep_max_heap这个过程,假设删除的是节点i,那么我只需要将节点i和最后一个元素交换,并且在节点i上调用keep_max_heep函数就可以了:
void delete_heep_node(int i) {swap(array[i], array[heap_size]);--heap_size;keep_max_heap(i);}
注意在该过程中不要忘了将堆的大小减一。
增加节点
增加堆中的一个节点相对容易,如图所示,假设堆中新增了一个节点16,那么该如何位置堆的性质呢?很简单,我们只需要将16和其父节点进行比较,如果不符合要求就交换,并重复该过程直到根节点为止,这个过程就好比水中的气泡上浮,有的资料也将这个过程形象的称为“shift up”,该过程的时间复杂度为O(logn)。
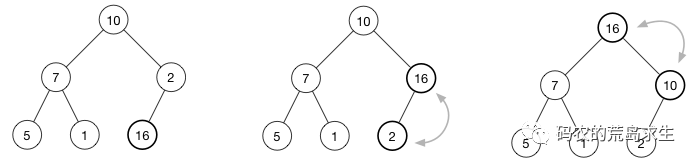
用代码表示就是如下add_heap_node函数:
void add_heap_node(int i){if (i == 0)return;int p = parent(i);if(array[i] > array[p]) {swap(array[i], array[p]);add_heap_node(p);}}
至此,关于堆的性质、堆的创建以及增删就讲解完毕了,接下来我们看一下堆这种数据结构都可以用来做些什么。
堆的应用
在这一节中我们介绍三种堆常见的应用场景。
排序
有的同学可能会有疑问,堆这种数据结构该如何来排序呢?
让我们来仔细想一想,对于大根堆来说其性质就是所有节点的值都比其左子树节点和右子树节点的值要大,那么我们很容易得出以下结论,对于大根堆来说:
堆中的第一个元素就是所有元素的最大值。
有了这样一个结论就可以将堆应用在排序上了:
-
将大根堆中的第一个元素和最后一个元素交换
-
堆大小减一
-
在第一个元素上调用keep_max_heap维持大根堆的性质
这个过程能进行排序是很显然的,实际上我们就是不断的将数组中的最大值放到数组最后一个位置,次大值放到最大值的前一个位置,利用的就是大根堆的第一个元素是数组中所有元素最大值这个性质。
用代码表示就如下所示:
void heap_sort(){build_max_heap();for(int i=heap_size-1;i>=1;i--){swap(array[0],array[i]);--heap_size;keep_max_heap(0);}}
执行完heap_sort函数后array中的值就是有序的了,堆排序的时间复杂度为O(nlogn)。
求最大(最小)的K个数
对于给定数组如何求出数组中最大的或者最小的K个数,有的同学可能觉得非常简单,不就是排个序然后就得到最大的或最小的K个数了吗,我们知道,排序的时间复杂度为O(nlogn),那么有没有什么更快的方法吗?
答案是肯定的,堆可以来解决这个问题,在这里我们以求数组中最小的K个值为例。
对于给定的数组,我们可以将数组中的前k个数建成一个大根堆,注意是大根堆,建成大根堆后array[0]就是这k个数中的最大值;
接下来我们依次将数组中K+1之后的元素依次和array[0]进行比较:
-
如果比array[0]大,那么我们知道该元素一定不属于最小的K个数;
-
如果比array[0]小,那么我们知道array[0]就肯定不属于最小的K个数了,这时我们需要将该元素和array[0]进行交换,并在位置0上调用keep_max_heap函数维护大根堆的性质
这样比较完后堆中的所有元素就是数组中最小的k个数,整个过程如下所示:
void get_maxk(int k) {heap_size = k; // 设置堆大小为kbuild_max_heap(); // 创建大小为k的堆for(int i=k;i<array.size();i++){if(array[i] >= array[0]) // 和堆顶元素进行比较,小于堆顶则处理continue;array[0] = array[i];keep_max_heap(0);}}
那么对于求数组中最大的k个数呢,显然我们应该建立小根堆并进行同样的处理。
注意使用堆来求解数组中最小K个元素的时间复杂度为O(nlogk),显然k<n,那么我们的算法优于排序算法。
定时器是如何实现的
我们要讲解的堆的最后一个应用是定时器,timer。
定时器相信有的同学已经使用过了,定义一个timer变量,传入等待时间以及一个回调函数,到时后自动调用我们传入的回调函数,是不是很神奇,那么你有没有好奇过定时器到底是怎么实现的呢?
我们先来看看定时器中都有什么,定时器中有两种东西:
-
一个是我们传入的时延,比如传入2那就是等待2秒钟;传入10就是等待10秒钟;
-
另一个是我们传入的回调函数,当定时器到时之后调用回调函数。
因此我们要做的就是在用户指定的时间之后调用回调函数,就这么简单;为做到这一点,显然我们必须知道什么时间该调用用户传入的回调函数。
最简单的一种实现方式是链表,我们将用户定义的定时器用链表管理起来,并按照等待时间大小降序链接,这样我们不断检查链表中第一个定时器的时间,如果到时后则调用其回调函数并将其从链表中删除。
链表的这种实现方式比较简单,但是有一个缺点,那就是我们必须保持链表的有序性,在这种情况下向链表中新增一个定时器就需要遍历一边链表,因此时间复杂度为O(n),如果定时器很多就会有性能问题。
那么该怎样改进呢?
初看起来,堆这种数据结构和定时器八竿子打不着,但是如果你仔细想一想定时器的链表实现就会看到,我们实际上要找的仅仅就是时延最短的那一个定时器,链表之所以有序就是为此目的服务的,那么要得到一个数组中的最小值我们一定要让数组有序才可以吗?
实际上我们无需维护数组的有序就可以轻松得到数组的最小值,答案就是刚学过的小根堆。
只要我们将所有的定时器维护成为一个小根堆,那么我们就可以很简单的获取时延最小的那个定时器(堆顶),同时向堆中新增定时器无需遍历整个数组,其时间复杂度为O(logn),比起链表的实现要好很多。
首先我们看一下定时器的定义:
typedef void (*func)(void* d);class timer{public:timer(int delay, void* d, func cb) {expire = time(NULL) + delay; // 计算定时器触发时间data = d;f = cb;}~timer(){}time_t expire; // 定时器触发时间void* data; // timer中所带的数据func f; // 操作数据的回调函数int i; // 在堆中的位置};
该定时器的定义非常简单,用户需要传入时延,回调函数以及回调函数的参数,注意在定时器内部我们记录的不是时延,而是将时延和当前的时间进行加和从而得到了触发定时器的时间,这样在处理定时器时只需要简单的比较当前时间和定时器触发时间的大小就可以了,同时使用i来记录该timer在堆中的位置。
至于堆我们简单的使用vector而不是普通的数组,这样数组的扩增问题就要交给STL了 :)
注意在这里定时器是从无到有一个一个加入到堆的,因此在向堆中加入定时器时就开始维护堆的性质,如下即为向堆中增加定时器add_timer函数:
void add_timer(timer* t){if (heap_size == timers.size()){timers.push_back(t);} else {timers[heap_size]=t;}t->i = heap_size;++heap_size;add_heap_node(heap_size-1);}
当我们删除定时器节点时同样简单,就是堆的节点删除操作:
void del_timer(timer* t){if (t == NULL || heap_size == 0)return;int pos = t->i;swap_pos(timers[pos], timers[heap_size-1]); // 注意不要忘了交换定时器下标swap(timers[pos], timers[heap_size-1]);--heap_size;keep_min_heap(pos); // 该函数实现请参见大根堆的keep_max_heap}
当我可以向堆中增加删除定时器节点后就可以开始不断检测堆中是否有定时器超时了:
void run(){while(heap_size) {if (time(NULL) < timers[0]->expire) // 注意这里会导致CPU占用过高continue; // 真正使用时应该调用相应函数挂起等待if (timers[0]->f)timers[0]->f(timers[0]->data); // 调用用户回调函数del_timer(timers[0]);}}
注意在这种简单的实现方式下,当堆中没有定时器超时时会存在while循环的空转问题从而导致CPU使用率上升,在真正使用时应该调用相关的函数挂起等待。
总结
堆是一种性质非常优良的数据结构,在计算机科学中有着非常广泛的应用,希望大家能通过这篇文章掌握这种数据结构。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号